金属簧片阻尼隔振器性能分析

王东衡，石秀东

(江南大学 机械工程学院，无锡 214122)

金属簧片阻尼隔振器性能分析

王东衡，石秀东

(江南大学 机械工程学院，无锡 214122)

建立了金属簧片隔振器振动系统的动力学模型，通过有限元计算得出摩擦力曲线，进一步采用动力学方程研究了系统在简谐激励和冲击激励下的响应。结果表明:电子机柜采用该隔振器，能使最大加速度降低72%，说明该隔振器具有良好的减振隔振和抗冲击性能，为干摩擦隔振器优化设计提供了理论依据。

隔振器;干摩擦阻尼;动态特性;非线性振动

在非线性振动研究领域，含有干摩擦环节的隔振、抗冲击隔振器能提供强的非线性阻尼，并能够有效的实现、控制和维修，其可靠性高。对于含干摩擦阻尼隔振减振系统的研究，国内外学者都进行了一定的研究，张强星等对干摩擦振动系统进行了简化，给出了非线性系统的响应计算［1］。颜肖龙等对含干摩擦振动系统的“无谐振”振动隔离进行了研究［2］。白鸿柏、黄协清等［3－4］对干摩擦振动系统在简谐激励和稳态Gaussian白噪声激励下的响应计算进行了研究，并对干摩擦模型和基于相应模型的响应计算方法进行了详细的综述［5］。周桐、万叶青等［6－7］对含干摩擦阻尼的钢丝绳隔振器进行了研究和分析。夏宇宏等对含干摩擦阻尼的金属橡胶隔振器进行了长期研究［8］。Liang、Wu、Oliveto等［9－12］基于干摩擦阻尼振动系统参数辨识进行了研究。Rigaud等［13］设计了干摩擦振动试验，在振动试验中考虑了粘性阻尼、干摩擦阻尼和弹性恢复力，动、静摩擦因数的不同，但动、静摩擦因数之间是与速度有关的线性关系。本文研究的金属簧片隔振器是用于舰载电子机柜的减振和抗冲击，主要从提高减振器隔振缓冲效果出发，研究和分析了其动态特性以及对其动态特性影响的主要结构，对于保证在恶劣环境下舰载设备系统的可靠性，具有重要的现实意义。

1 金属簧片隔振器力学分析

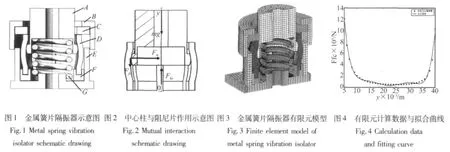
金属簧片隔振器的结构见图1，图中:A中心柱、B帽盖、C结构阻尼片、D阻尼片、E底座、F底槽座、G弹簧。阻尼片的底部由底座槽约束固定，上端与结构阻尼片约束，工作时机柜置于中心柱之上，与中心柱螺栓连接。隔振系统的刚度主要由金属弹簧和阻尼片提供，垂向刚度由金属弹簧和阻尼片提供，横向刚度由阻尼片提供，金属弹簧为圆柱螺旋弹簧是线性弹簧。系统阻尼主要为干摩擦阻尼和粘性阻尼。

阻尼片带有弧形结构，具有几何非线性特性。本文采用有限元法求解簧片阻尼片与中心柱之间的相互作用力。利用LS－DYNA程序建立金属簧片隔振器动力学有限元分析模型(见图3)，各组件均采用Solid164(8节点6面体单元)，单元属性设为常应变;各组件的材料模型和具体属性参数见表1［14］。

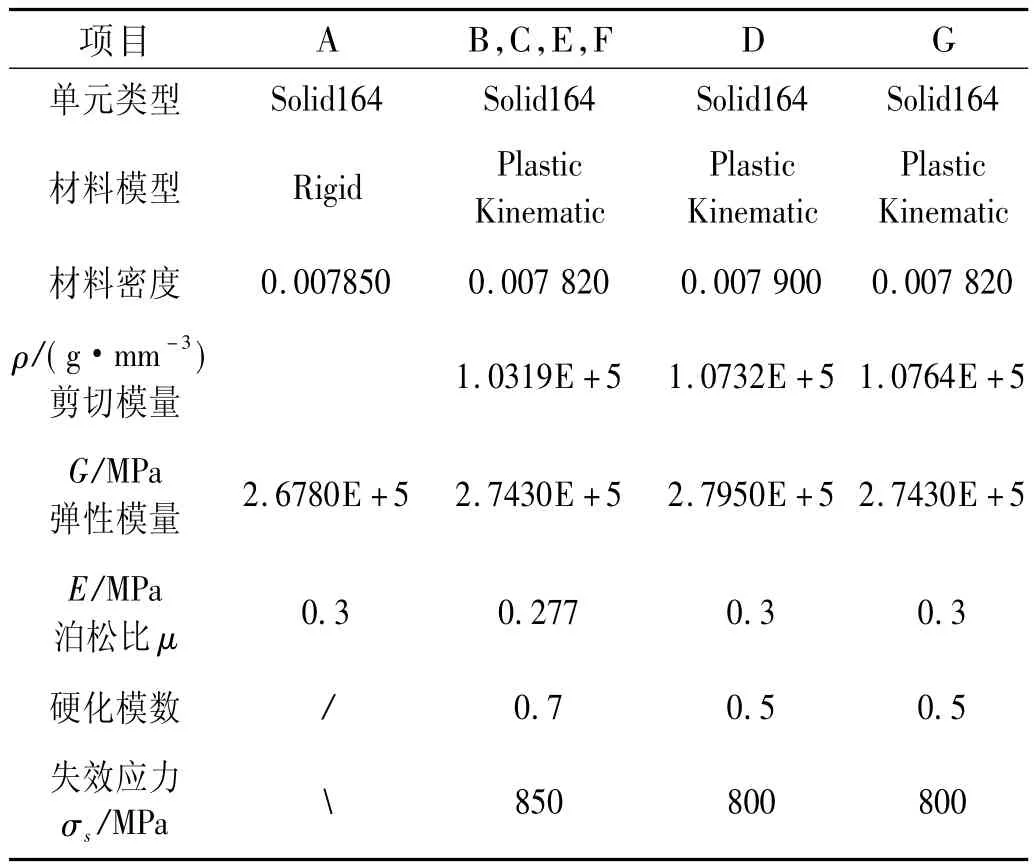
表1 单元类型和材料属性Tab.1 Element type and material properties

在本计算模型中，各界面接触均采用自动的面对面接触算法(AUTOMATIC SURFACE TO SURFACE CONTACT)。在定义界面接触参数时，中心柱与阻尼片接触界面静摩擦系数为0.25，动摩擦系数为0.2，其它接触对静动摩擦系数均为0.15，同时接触刚度和接触深度参数定义为0.1和0。

图4是有限元分析得到中心柱与阻尼片摩擦接触力Ffc与y的关系图。图中星点是计算数据，实线是拟合曲线。由图可以看出:曲线中间比较平坦，两边比较陡，说明当中心柱处于阻尼片中间位置时，相互作用的正压力较小，产生的摩擦阻尼也较小;当中心柱移动到阻尼片两端时，正压力急剧增大，两者产生的摩擦阻尼同时急剧增大，能最大限度的消耗冲击能量。

由金属簧片阻尼隔振器特点，激励幅值较小时，阻尼片与中心柱之间静摩擦力较大，使二者不能产生相对运动，而不产生峰值共振。当激励幅值较大或遭受强冲击时，阻尼片两端提供强滑动摩擦阻尼，能有效抑制共振峰值。由以上分析表明，这种带曲率的阻尼片耦合干摩擦阻尼，在小载荷激励下，将具有好的隔振传递率，在遭受大冲击时具有强阻尼，能有效的起到抗冲击作用。

2 金属簧片阻尼隔振器动态特性分析

2.1 金属簧片阻尼隔振器在简谐激励下动态分析

金属簧片隔振器，其动态特性主要由振动系统刚度、阻尼、外界激励及预载荷决定。建立隔振系统的力学模型见图5，此动力学模型的振动微分方程如下:

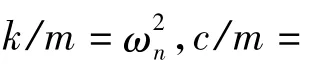
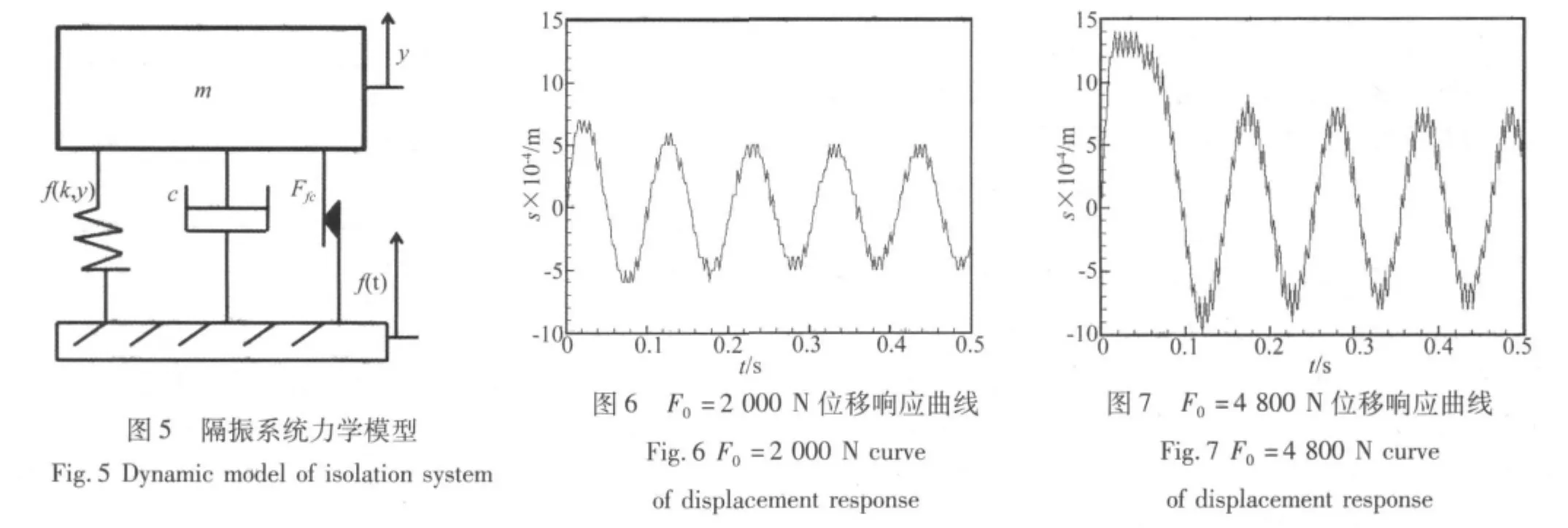
图6表明，激励力幅值较小时，阻尼片中间段提供弱阻尼，隔振系统经过几个周期进入稳定状态，隔振系统具有好的振动传递率。图7表明，当激励力幅值较大时，由第一个周期位移响应曲线可以看出，阻尼片在强激励时能提供强的干摩擦阻尼，使隔振系统很快进入稳定状态。初始时刻，隔振系统位移响应的频率和幅值变化剧烈，到稳态时其位移幅值和响应频率基本保持不变。对照图6、图7，相同激励频率但激励力幅值不同时，由于阻尼片提供强非线性干摩擦阻尼，隔振系统位移响应幅值不成线性增加，强激励位移响应峰值比弱激励位移响应峰值延后。

2.2 金属簧片阻尼隔振器在冲击激励下动态分析

有限元法和动力学理论结合，可以有效解决冲击动力学问题。把方程(1)变换成标准的动力学方程:

采用有限元法求解动力学中的接触摩擦问题，要考虑材料的屈服失效。因此按以下方式定义摩擦力［15］:fn为从节点ns的法向屈服力，则最大摩擦力为为摩擦系数。设在上一时刻tn从节点ns的摩擦力为Fn，则此时刻tn+1可能的摩擦力(试探摩擦力)为F*=Fn－kΔα，k为界面刚度，Δα为从节点移动增量，此时刻的摩擦力按公式(5)确定。

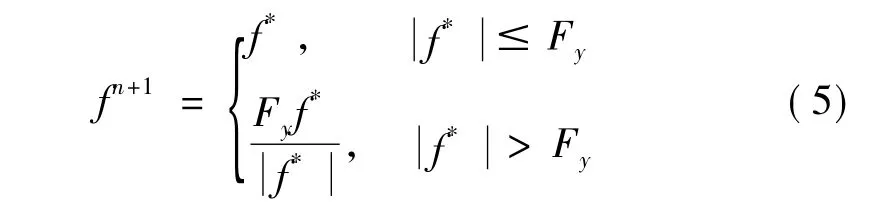
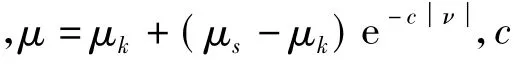
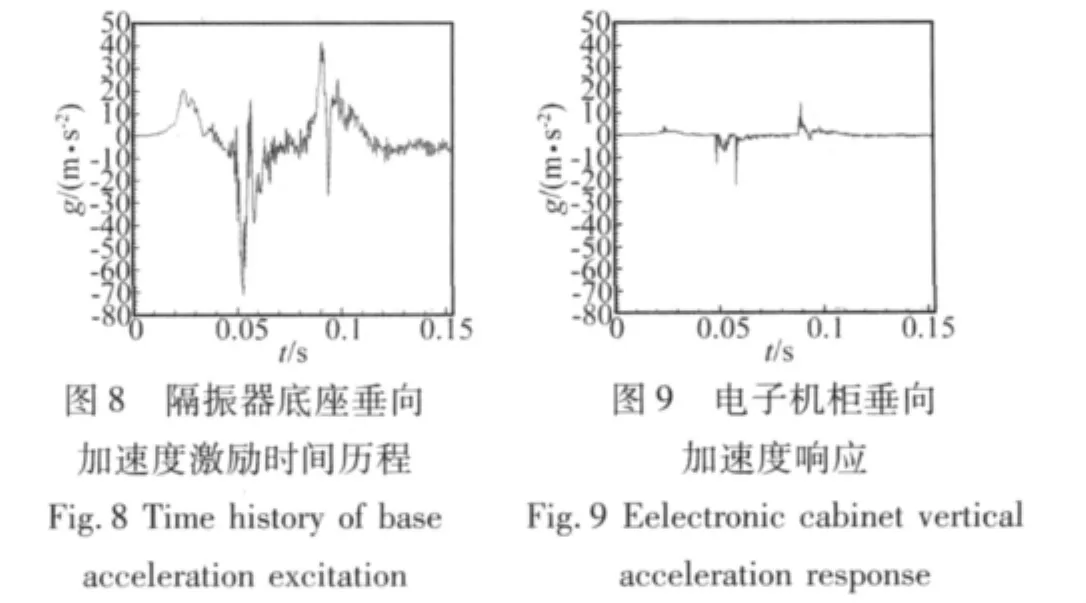
综合各种非线性因素，利用显示中心差分法，通过有限元迭代计算隔振系统冲击响应。本文金属簧片隔振器承载电子机柜为40 kg，图8是某一次实测的舰船在受水雷袭击时舰体给机柜的加速度冲击激励，其最大加速度峰值向上是43 g，向下是77 g。图9是采用金属簧片隔振器后，利用有限元法计算上述等效激励作用到机柜上的加速度响应。从图中可以看出，通过金属簧片隔振器减振隔振，使作用到机柜上的最大加速度向上降至12 g，向下降至21 g(g为重力加速度单位)。说明该金属簧片隔振器的减振隔振效果明显，特别是在遭受大冲击时，具有优良的抗冲击性能。

3 结束语

本文建立了金属簧片隔振器承载电子机柜时的动力学模型，结合实体有限元法，分析了该非线性力学模型的动态特性，探索了一种金属簧片隔振器动态特性的分析方法;分析了隔振系统简谐激励时不同激励力幅下的位移响应，以及冲击激励下的加速度响应。结果表明:电子机柜采用金属簧片隔振器减振隔振后，在测试冲击下，能使向上最大峰值冲击加速度响应降为原来的27.9%，向下最大峰值冲击加速度降为原来的27.3%，说明金属簧片隔振器具有优良的减振隔振和抗冲击性能。本文的研究为干摩擦隔振器动态参数优化及进一步实验研究提供了理论依据。

［1］张强星，Sainsbury M G.干摩擦振动系统的简化［J］.振动与冲击，1987，6(1):42 －58.

［2］颜肖龙，张以彬，等.无谐振隔振原理的理论分析与应用［J］.东南大学学报，1998，28(4):128 －132.

［3］白鸿柏，黄协清.干摩擦振动系统响应计算方法研究［J］.振动工程学报，1998，11(4):472 －475.

［4］白鸿柏，黄协清.干摩擦振动系统随机激励响应Krylow_Bogoliubow计算方法［J］.振动与冲击，2000，19(2):83－85.

［5］白鸿柏，黄协清.干摩擦振动系统响应计算方法研究综述［J］.力学进展，2001，31(4):527 －534.

［6］周 桐，刘青林.钢丝绳隔振系统简化模型分析［J］.振动与冲击，2007，26(9):55 －59.

［7］万叶青，范立民，等.钢丝绳隔振器非线性特性分析［J］.振动与冲击，2007，26(7):46 －49.

［8］夏宇宏，姜洪源，等.金属橡胶隔振器抗冲击性能研究［J］.振动与冲击，2009，28(1):72 －75.

［9］Liang J W.Identifying Coulomb and viscous damping from free-vibration acceleration decrements［J］.Journal of Sound and Vibration，2005，282:1208 －1220.

［10］ Liang J W.Damping estimation via energy-dissipation method［J］.Journal of Sound and Vibration，2007，307:349 －364.

［11］ Wu Z，et al.Identification of non-linear viscous damping and Coulomb friction from the free response data［J］.Journal of Sound and Vibration，2007，304:407 －414.

［12］ Oliveto N D，Scalin G，Oliveto G，et al.Dynamic identification of structural systems with viscous and friction damping［J］.Journal of Sound and Vibration，2008，318:911 －926.

［13］ Rigaud E，et al.An original dynamic tribotest to discriminate friction and viscous damping［J］.Tribol Int(2009)，DOI:10.1016/j.triboint.2009.06.011.

［14］胡德罗，胡小舟.现代工程材料手册［M］.北京:宇航出版社，1992.

［15］ Hallquist J O.LS-DYNA theory manual［M］.Liver-more:Livermore Software Technology Corporation，2006.

System performance analysis for a metal plate spring vibration isolator

WANG Dong-heng，SHI Xiu-dong

(School of Mechanical Engineering，Jiangnan University，Wuxi 214122，China)

Dynamic model of a metal plate spring vibration isolator system was built up.The friction force curve was calculated using finite element method.Through calculating the dynamic equation，the responses of the system under different harmonic exciting forces and impacts were studied.The results indicated that when an electronic cabinet is placed on the isolator，the system maximum acceleration reduces by 72%;the metal plate spring vibration isolator has good vibration damping and impact-resistance performance.This study provided a theoretical basis for optimal design of dry friction absorbers.

vibration isolator;friction damper;dynamic performance;nonlinear vibration

O322;TH113.1

A

2009－12－30 修改稿收到日期:2010－03－31

王东衡 男，硕士生，1983年12月生