电机传动机构动力学建模、仿真与实验验证

潘 博，孙 京，娄丽芬

(1.中国空间技术研究院，北京 100094;2.中航工业北京曙光电机厂，北京 100028)

电机传动机构动力学建模、仿真与实验验证

潘 博1，孙 京1，娄丽芬2

(1.中国空间技术研究院，北京 100094;2.中航工业北京曙光电机厂，北京 100028)

建立正确的电机动力学模型是分析系统稳定性和动态特性的基础。考虑到用电设备工作时的脉冲电流是发电机传动机构扭转振动的主要激励源，利用集中参数法建立了某型交流发电机的动力学模型，并在MATLAB环境下对其进行动态仿真分析，得到脉冲电流作用下弹性轴冲击扭转振动的力矩曲线与扭转角曲线。通过对仿真结果的对比分析，发现适当增大弹性轴的轴径，可以有效缓解弹性轴扭转力矩的振动峰值，并提高系统的频率裕度。最后，通过动态测试实验，验证了电机动力学模型与仿真结果的有效性。

发电机;传动机构;动力学建模;数值仿真;实验验证

交流发电机是航空飞行器、船舶等运载工具中任务系统电能的主要来源。它由大功率动力源(如航空发动机、船舶柴油机等)驱动，将机械能转化为交流电［1，2］。因此，发电机稳定、安全可靠的运行是保证任务系统甚至载机正常工作的关键。而建立正确的电机动力学模型，对于计算系统的稳定性或分析系统的动态特性是至关重要的［3］。

由于发电机的输出效率依赖于用电设备的需求及其运行规律。因此，用电设备产生的时变载荷是发电机的主要扰动源［4］。而常规电机传动机构的设计，是在稳态运转假设下，利用有效载荷值进行刚度与强度的设计与校核。但电机工作中，通常存在时变载荷甚至瞬态的苛刻载荷。这便使设计裕度降低甚至丧失，因此往往导致传动机构的非正常破坏。如本文中涉及的交流发电机弹性轴就出现了累积4次的断轴故障。此外，由于轮齿柔性、齿间摩擦和齿侧间隙的存在，传动机构中齿轮、花键等轮齿的啮合特性也是影响系统动力学特性的关键因素［5，6］。

本文以某型发电机为研究对象，如图1所示。该发电机为风冷式三级旋转整流器式无刷结构，参见图2。为保证发电机工作的可靠性，传动机构采用了复合轴系的结构，复合轴系由空心轴和弹性轴组成。其中起断裂保护作用的弹性轴，如图3所示，其中段轴径为12.5 mm，通过两端外花键与输入齿轮和发电机转子空心轴的内花键配合，从而传递动力。

本文针对载机用电设备工作时具有脉冲电流的特性，进行交流发电机的动力学建模，模型中考虑了传动轴的柔性、花键的柔性及啮合非线性。并模拟机构的真实受力情况，在MATLAB环境下，对其进行动态仿真分析，得到在脉冲电流激励下，弹性轴扭转冲击振动的力矩曲线与扭转角曲线。通过对计算与实验结果的对比，分析了影响系统扭转振动特性的主要因素及关键参数，为弹性轴的改进设计提供理论依据和动态分析工具。

1 动力学建模

为便于动态分析与简化计算，本文采用集中参数法建立电机的低阶动力学模型，如图4所示。

经有限元分析，输入齿轮与发电机转子的扭转刚度至少在弹性轴扭转刚度的一个量级以上，因此可假设为刚体。

1.1 数学模型

根据图4所示的动力学模型，得到相应的数学模型为:

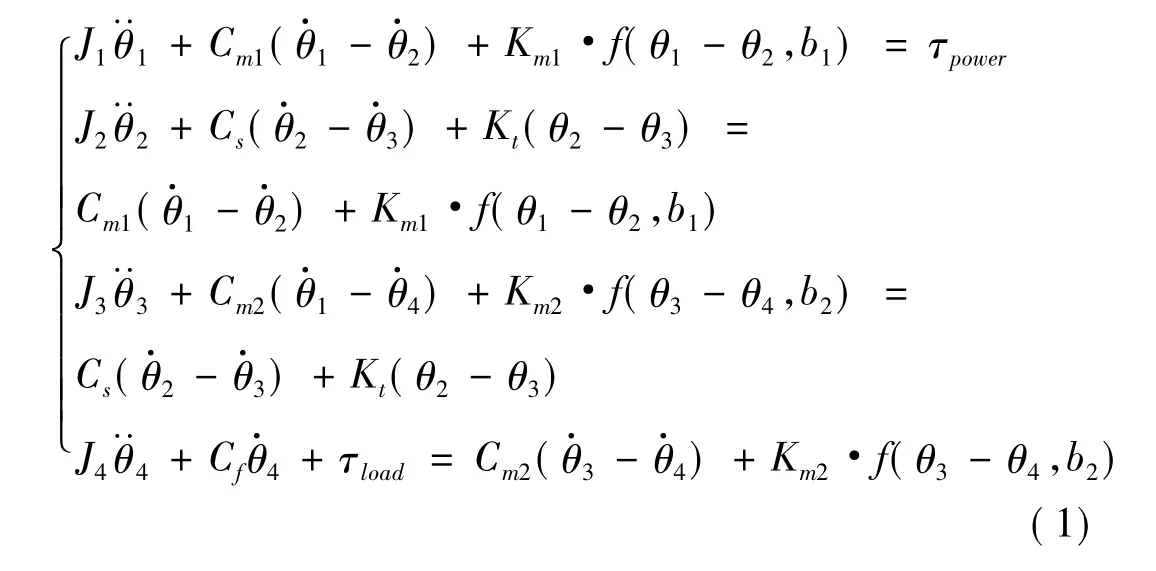
其中，τpower和τload分别为动力源输入力矩和负载反力矩，其他参数定义见图4。f(x，b)为间隙函数，其传统分段线性化表达式为:

但式(2)不利于数值求解，由于运算过程中需要反复调用该子函数，造成求解速度大幅减低，且由于造成刚度矩阵无法分离，往往导致求解发散。本文利用双曲正切函数tanh的特有性质，采用一种连续函数对式(2)描述的分段线性函数进行近似，如式(3)所示:

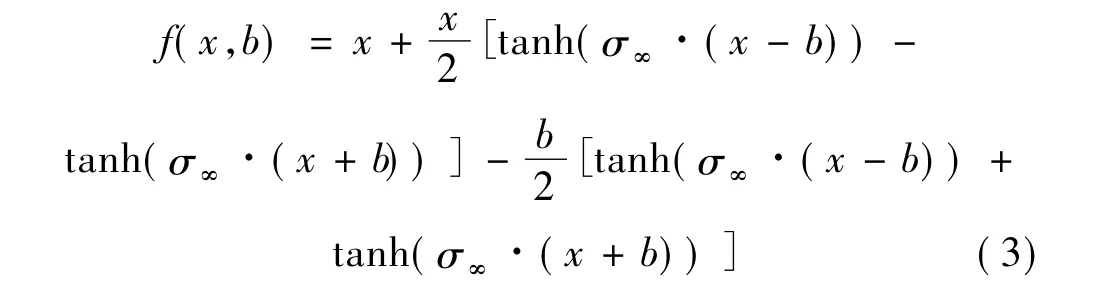
其中，2b为间隙值，σ∞为放大系数。当σ∞为间隙的1 000倍以上时，已经有很好的近似。并且式(3)可以进行分解，将非线性项移至方程的右侧作为伪激励。

本文采用大增益比例控制环节来模拟大功率恒定转速的动力源(如航空发动机)的动力学特性，如式(4)。

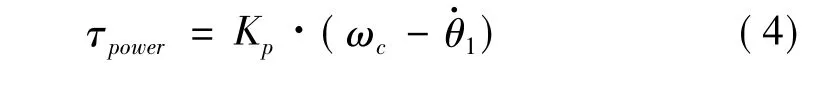
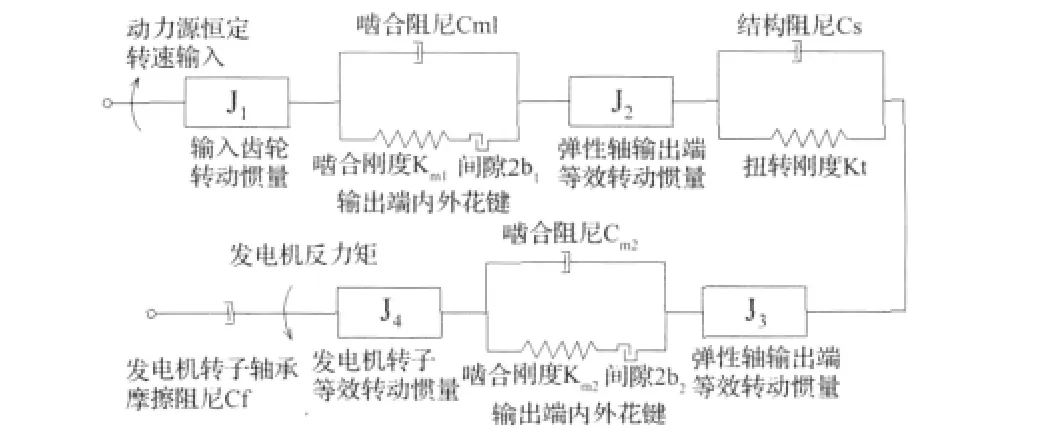
图4 发电机动力学模型Fig.4 Dynamic model of the generator

这里选取比例增益为Kp=2 000 N·m·s/rad。此时，发动机的转速可稳定保持在ωc=8 000 r/min，波动极小。

1.2 模型参数的计算

模型中内外花键的啮合刚度，由 GB/T 3480－1997［7］中提供的方法进行计算。其中，输入端为1.337 1×106N·m/rad，输出端为 5.691 6 ×105N·m/rad。啮合阻尼采用文献［8］中的经验公式进行估算。利用有限元方法计算出弹性轴的扭转刚度为:686.948 0 N·m/rad(该值不包括扭矩传感器的柔性，仿真计算中考虑了扭矩传感器的柔性)。弹性轴的结构阻尼采用NASA的经验公式［9］进行估算。各构件的转动惯量、重心位置，由SOLIDWORKS软件建立三维实体模型后计算得出。其中弹性轴两端的等效转动惯量由质心不变原则进行分配。

1.3 载荷谱的确定

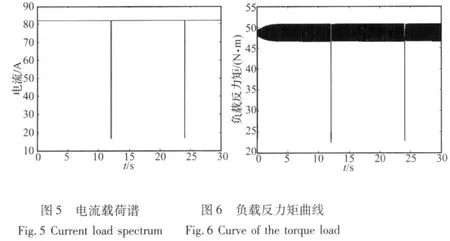
根据用电设备工作过程中电流脉冲实的测数据，发电机的外载荷曲线为周期为12 s、脉冲宽度120ms的间歇式周期脉冲，如图5所示:

由于电流脉冲作用的同时，不仅会引起发电机反力矩的脉冲变化，瞬时的转速也会发生变化，从而得到考虑转速扰动下的发电机反力矩曲线，如图6所示。其中，发电机反力矩的计算考虑了不同输出功率下发电机的效率值。

2 数值仿真

发电机动力学模型的建立和数值仿真在MATLAB环境下完成。为提高计算效率和计算精度，采用精细积分方法［10］，进行仿真计算，积分步长为 0.5 ms。该方法具有计算速度快、无条件稳定以及精度高等优点。

2.1 原弹性轴动态特性分析

假设初始条件为各构件均以8 000 r/min的转速旋转，在间歇式周期脉冲载荷作用下，原弹性轴的输入端外花键扭转力矩、弹性轴的扭转角和扭转力矩时程曲

线，如图7～图9所示:从图7中可以看出，输入端外花键扭转力矩具有200 N·m以上的瞬态负冲击力矩，这与弹性轴输入端外花键非啮合面出现磨损现象是吻合的，如图10所示。其原因是用电设备工作时产生的负向电流脉冲，造成弹性轴与输入齿轮之间产生反向冲击转矩，从而引起弹性轴外花键的非啮合齿面产生磨痕。由此，也可看出用电设备工作时反复出现的冲击电流是弹性轴产生扭转冲击振动的主要原因。

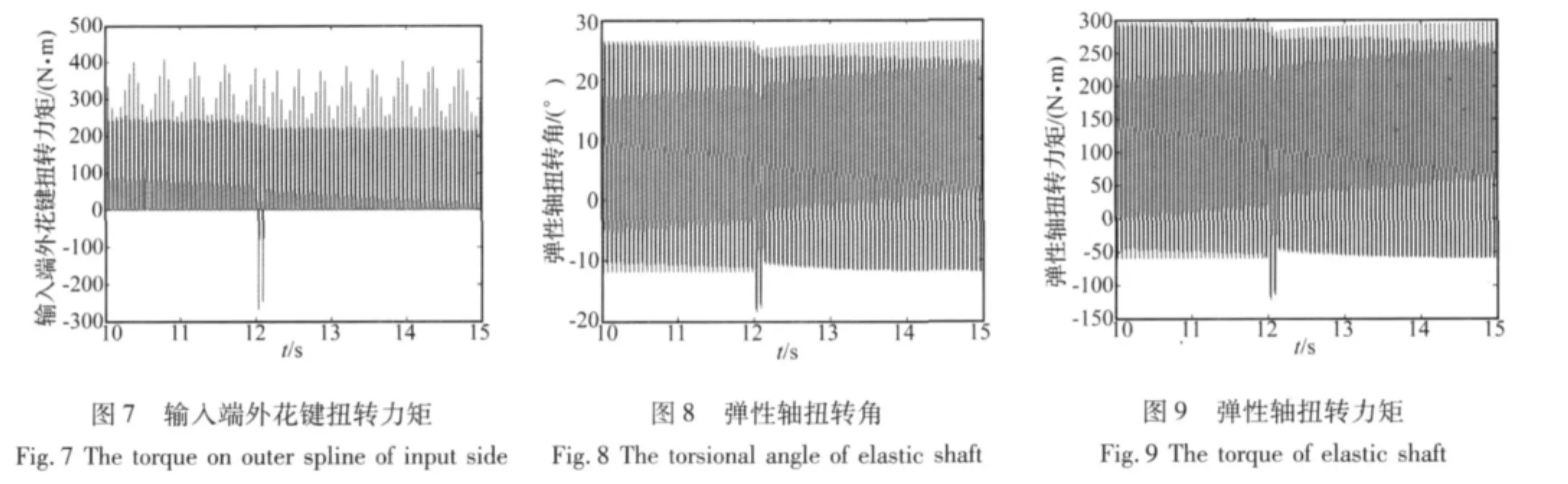
图10 输入端外花键磨损情况Fig.10 The wear condition on outer spline of input side

此外，不考虑瞬态峰值扭矩，在300 N·m等幅扭矩峰值作用下，通过有限元分析得到弹性轴最大剪切应力为842.27 MPa。而弹性轴的设计许用扭转剪切应力值［τ］为550 MPa。可见，此时弹性轴的扭矩幅值已超过该极限，这也解释了屡次出现非正常断轴故障的原因。

2.2 改进弹性轴的动态特性分析

为改进弹性轴乃至整个电机系统的动力学特性，将弹性轴的轴径加粗至14.5mm。改进后的弹性轴，扭转刚度增至1.273 5×103Nm/rad，而强度仍满足对动力源起断裂保护作用的要求。其输入端外花键扭转力矩、扭转角和扭转力矩时程曲线，如图11～图13所示:

不考虑瞬态峰值扭矩，在200 N·m等幅扭矩峰值作用下，通过有限元分析得到改进的弹性轴最大剪切应力为343.23 MPa，小于设计许用剪切应力值，满足动态的设计要求。可见，增大弹性轴的轴径，可以有效缓解弹性轴的扭转力矩振动峰值。但弹性轴的轴径也不易过粗，因为考虑到发电机的破坏保护作用，从强度方面将，弹性轴需要先断。

2.3 弹性轴频谱特性分析

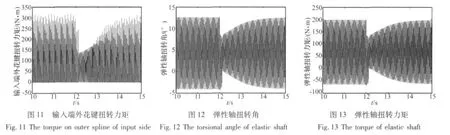
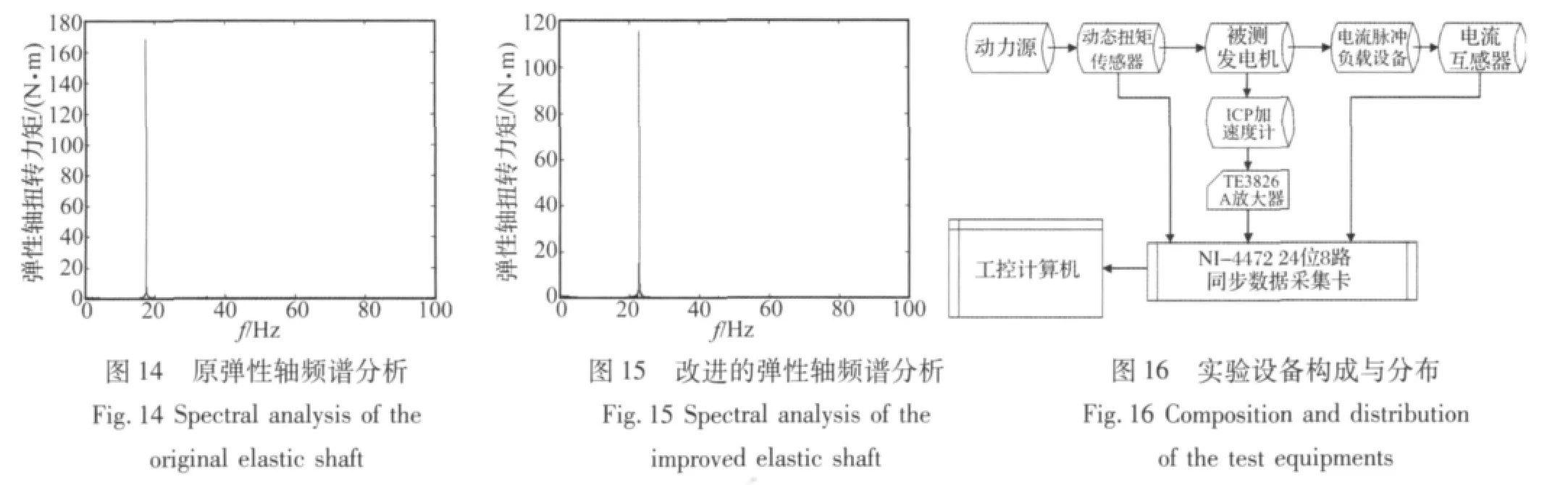
不同的弹性轴直径对应不同的扭转刚度，通过对仿真结果进行频谱分析，得到原弹性轴和改进的弹性轴扭转振动的频谱曲线，如图14、图15所示。其扭转振动频率分别为17.37 Hz和22.63 Hz。通过对比分析可知，改进后，系统的振动频率提高30.2%以上，且振动幅值要小得多，约减小30%。因此，改进后的弹性轴较原弹性轴具有更大的力矩裕度(相对许用扭矩值)和频率裕度(相对动力源某主要构件18 Hz的转速)。

3 实验验证

该交流发电机的动态扭转冲击实验台由大功率动力驱动设备、电流脉冲负载设备、动态扭矩传感器、电流互感器、动态测量分析与记录系统等组成，如图16所示。其中，动力驱动设备采用160 kW交流电动机，如图17所示。电流脉冲负载设备为发电机运行提供脉冲扭矩激励源，通过改变脉冲的幅值和脉冲的周期改变激励强度。并利用动态扭矩传感器(北京普瑞萨思测控技术有限公司生产，型号 PS－T2，量程 ±500 Nm，精度0.25%)，测量弹性轴的扭转力矩值，包括:冲击扭矩峰值、扭转振动幅值、频率等。

电流脉冲负载设备为270 V的ZFW－65直流负载箱，如图18所示。采用计算机控制的继电器板卡替代JK1－JK12手动开关，如图19所示，对脉冲电流的幅值进行自动控制，同时采用开关量测量板卡对JK1～JK12开关状态进行测量与记录。通过控制图19中所示的R9～R13电阻的导通，可以实现对负载设备1 A～31 A的电流值下限的控制;通过控制图19中所示的R1～R8电阻的导通，可以达到控制负载设备1 A～110 A电流波动幅值的目的;而通过脉冲控制器对电流的导通时间和断开时间的预设置，实现对正负电流脉冲的宽度的控制，如控制脉冲宽度为毫秒级或秒级。并通过RS232接口对脉冲控制器进行工作状态查询、脉冲工作模式的启动与停止和脉冲工作模式的设置(如正、负脉冲模式)。电流值由相电流互感器电路中串联的20 Ω电阻两端的电压值，经转换间接测得(量程200 A，精度2%)。

测得在用电设备脉冲电流的作用下，电机扭转振动的时域曲线及频谱特性，如图20～图23所示。

由于所建立的模型为低阶等效系统，因此无法得到实际系统的高阶频率。但工程上主要关心系统的一阶振动频率，而对于改进前、后的弹性轴，仿真结果与实测数据的一阶振动频率的相对误差分别4.14%和12.98%，如表1所示，且时域曲线的振动幅值基本一致。因此，可以认为该模型在工程应用上具有足够的精度。从而验证了文中动力学模型与仿真结果的正确性。

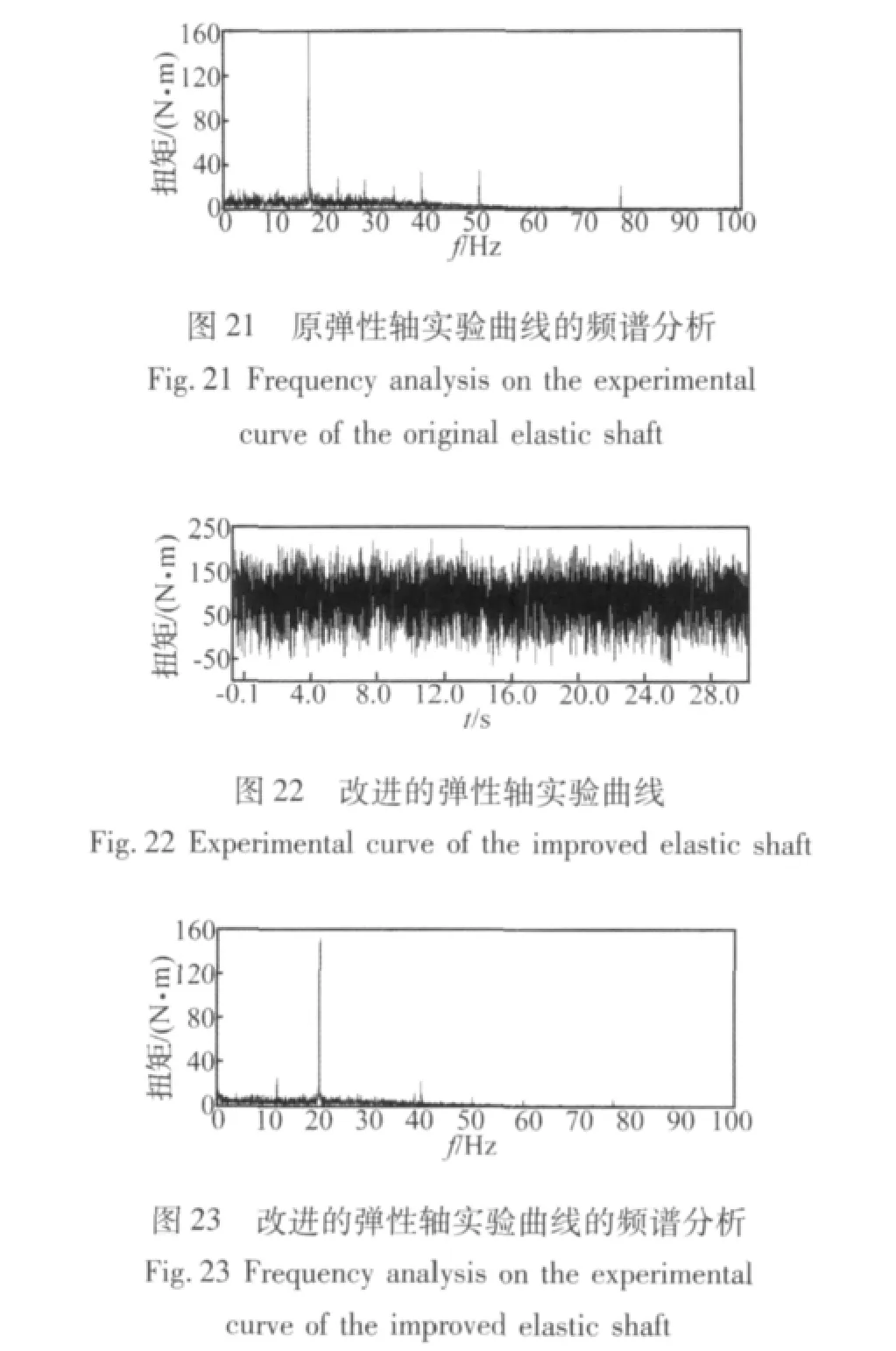
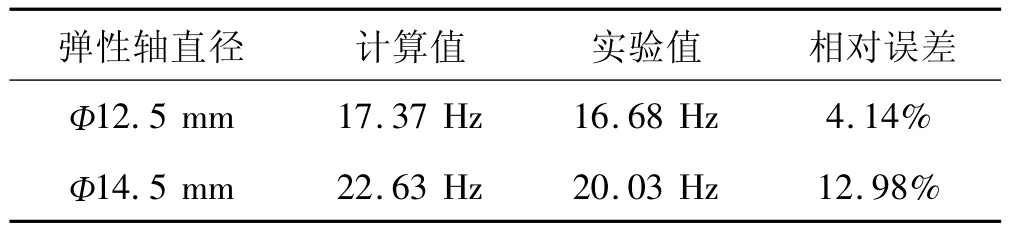
表1 弹性轴扭振频率计算值与实验值对比Tab.1 Comparison of the calculated values with the experimental data of the torsional vibration frequencies of the elastic shafts

4 结论

本文针对用电设备在工作时具有脉冲电流的特性，进行交流发电机的动力学建模，并在MATLAB环境下对其进行动态仿真分析，得到在脉冲电流激励下，弹性轴冲击扭转振动的扭矩曲线与扭转角曲线，通过对计算结果与实验数据进行对比分析，得到如下结论:

(1)发电机弹性轴的扭转振动的来源是用电设备工作时的脉冲电流。间歇式周期脉冲作用时，原弹性轴的最大剪切应力已超过许用的剪应力极限，这是造成原弹性轴发生多次非正常断裂的原因。

(2)原弹性轴的输入端外花键扭转力矩曲线中具有近200 N·m以上的瞬态负冲击力矩，此结果解释了弹性轴输入端外花键非啮合面出现磨损现象的原因。

(3)增大弹性轴的轴径，可以有效缓解弹性轴的扭转力矩振动峰值。改进后的交流发电机弹性轴较原弹性轴具有更佳的动态特性(如振幅减小很多)以及较大的力矩裕度和频率裕度。

［1］TantawyA， Koutsoukos X， Biswas G. AircraftAC Generators:Hybrid System Modeling and Simulation［C］.International Conference on Prognostics and Health Management，2008.

［2］李东辉，张均东，何治斌.教学实习船电力系统建模与仿真［J］.上海交通大学学报，2008，42(2):190－191.

［3］Vicol L， ViorelIA， Iancu V. Identification ofthe Synchronous Generator Parameters by Standstill Tests［C］.6th International Conference on Electromechanical and Power Systems，2007:138 －141.

［4］Fodor A，Magyar A，Hangos K M.Dynamic Modeling and Analysis of a Synchronous Generator in a Nuclear Power Plant［C/OL］.10th PhD Workshop on Systems and Control，University of Pannonia，2009［2009 －11 －28］.http://as.utia.cas.cz/files/104.pdf..

［5］郭家舜，王三民，刘海霞.某新型直升机传动系统弯－扭耦合振动特性研究［J］.振动与冲击，2009，28(10):132－140.

［6］郭 磊，郝志勇，蔡 军，等.汽车变速箱齿轮传动系动力学振动特性的研究［J］.振动与冲击，2010，29(1):103－107.

［7］GB/T 3480－1997渐开线圆柱齿轮承载能力计算方法［S］.

［8］孙智民，季林红，沈允文.2K－H行星齿轮传动非线性动力学［J］.清华大学学报(自然科学版)，2003，43(5):636－637.

［9］ Hsiang-Hsi(Edward)Lin，Ronald L.Huston，John J.Coy.On Dynamic Loads in Parallel Shaft Transmissions［R］.NASA Technical Memorandum 100180，1987，12:1 －14.

［10］裘春航，吕和祥，蔡志勤.在哈密顿体系下分析非线性动力学问题［J］.计算力学学报，2000，17(2):127－129.

Dynamic modeling，simulation and test verification for a drive mechanism of a generator

PAN Bo1，SUN Jing1，LOU Li-fen2

(1.China Academy of Space Technology，Beijing100094，China;2.Beijing Shuguang Electrical Machinery Factory of Aviation Industry，Beijing 100028，China)

A correct dynamic model of a generator system is the foundation analyzing its stability and dynamic characteristics.The current impulse in consumer equipments is the major excitation source of torsional vibration of the drive mechnism of the generator.Considering such a current impulse，the dynamic model was established with the lumped parameter method and simulated using MATLAB.And the comparative analysis of the simulation results was carried out.It showed that if the diameter of the shaft is properly increased，the peak torque of torsional vibration of the elastic shaft can be effectively alleviated and the frequency margin increases.The validity of the dynamic model and the simulation results was verified with dynamic tests.

generator;drive mechanism;dynamic modeling;numerical simulation;test verification

V233.1;TB123

A

2009－12－09 修改稿收到日期:2010－04－12

潘 博 男，博士，1982年3月生