含任意直线型裂纹的直角域中圆柱夹杂对SH波的散射

齐 辉，杨 杰，李宏亮，杨在林

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)

含任意直线型裂纹的直角域中圆柱夹杂对SH波的散射

齐 辉，杨 杰，李宏亮，杨在林

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)

采用Green函数及复变函数方法研究了SH波作用下直角域内任意直线型裂纹对圆柱弹性夹杂的影响。首先，取含有圆柱弹性夹杂的直角域内任意一点承受时间谐和的出平面线源荷载作用时的位移函数基本解作为适合Green函数;其次，利用裂纹切割技术构造裂纹，并写出圆柱夹杂与裂纹同时存在时的位移场和应力场;最后，给出圆柱弹性夹杂动应力集中系数的算例和结果，并讨论了裂纹的存在对动应力集中系数的影响。

直角域;圆柱夹杂;任意直线型裂纹;Green函数;动应力集中系数(DSCF)

缺陷广泛存在于天然介质和工程材料中，同时，各种缺陷的存在必然会影响材料的宏观力学行为，如地震现象、地震监测、冲击下材料和结构的响应等。在动力荷载作用下，含有缺陷的各种材料和结构表现出某些特殊的性质，例如缺陷处产生应力集中现象，从而导致材料的破坏。因此，为了满足理论及工程上的需求，研究各种缺陷的动力响应等问题具有十分重要的意义。由于弹性波的散射能够很好的解释材料受到冲击荷载时波的传播问题，同时SH波作为比较简单的模型，被广泛的应用工程实际问题中，而且起着越来越重要的地位［1～3］。然而，在已发表的诸多文章中，研究SH波作用下各种缺陷的响应问题多集中在全空间和半空间中［4～6］，只有少数人［7，8］对直角域中含缺陷的问题进行了研究。本文在文献［9～11］的基础上，利用Green函数及复变函数等方法研究了含任意直线型裂纹的直角域中圆柱弹性夹杂对SH波的散射问题，并讨论了裂纹对圆柱夹杂的影响。

1 问题的表述

圆柱弹性夹杂对SH波的散射模型如图1所示，在直角平面内存在一条长度为b的任意直线型裂纹。直角空间Ⅰ中介质的密度和剪切波速分别为ρ1和c1，圆柱夹杂的密度和剪切波速分别为ρ2和c2。圆柱夹杂圆心到水平边界和垂直界面的距离分别为h和d。简谐平面SH波以入射角α0入射到直角域。

图1 含任意直线型裂纹及圆柱夹杂的直角域模型Fig.1 The model with an arbitrary beeline crack and a cylindrical inclusion in right-angle plane

2 Green函数

满足控制方程(1)和边界条件(3)的位移场基本解，有两部分构成:直角平面区域内线源荷载产生的扰动和圆柱形弹性夹杂所激发的散射波。

对于线源荷载 δ(z－z0)在一个完整的直角域内的扰动，可将其视为入射波G(i)，在该问题中由于直角平面区域自由表面的存在，出平面线源荷载的扰动产生的弹性波将会在圆柱夹杂和直角平面区域自由表面上发生多次散射和反射，致使能满足直角平面区域自由表面上应力自由边界条件的波场的解析解很难给出。为了克服这一难点，利用“镜像法”，将直角区域对称于垂直边界左延拓为半无限空间，如图3所示，并引入复数坐标系(z'，')，z'=z+2d，因此等效的入射波可以表述为:

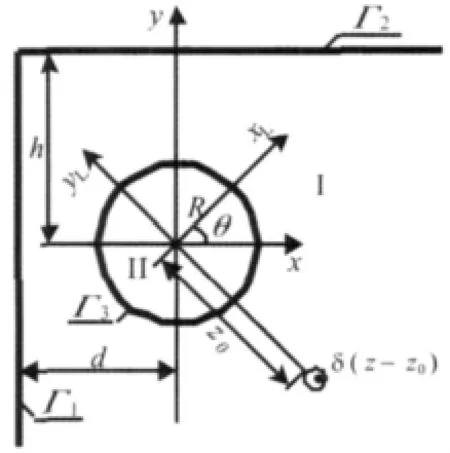
图2 出平面线源荷载作用的直角域模型Fig.2 The right-angle plane model impacted by a line source force

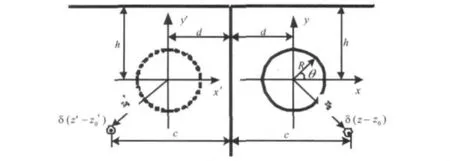
图3 直角平面区域镜像为半无限空间模型Fig.3 Transforming model from the right-angle plane to the half space

相应的，由于水平表面的存在而产生的等效反射波场为:

由于圆柱形弹性夹杂所激发的散射波将会在圆柱夹杂和直角平面区域自由表面上发生多次反射，故仍需采用镜像叠加原理及坐标移动技术将其构造为:

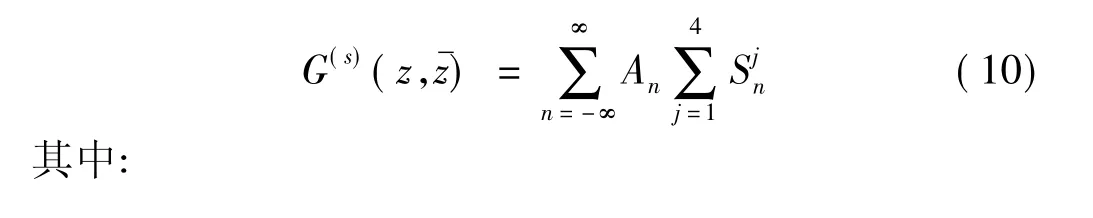
利用圆柱形弹性夹杂边界r=R位移和应力连续性条件:

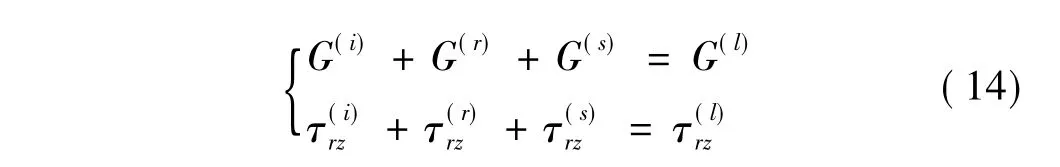
得到确定待定系数An，Bn的方程组，经整理后方程组可以表述为:

为得到未知系数 An，Bn，(n=0，±1，±2，…)，对方程组(16)通过有项截断得到有限未知数的方程组并求解。在本文算例中，对于上述无穷代数方程组中的每一个级数项分别选取7项即可很好满足预先给定的计算精度(10－6)。

根据SH波散射的对称性及叠加原理，由出平面线源荷载的扰动和由圆孔所激发的散射波组成的总波场能满足直角平面区域边界应力自由条件.此时介质内的总波场，即求解问题的Green函数为:

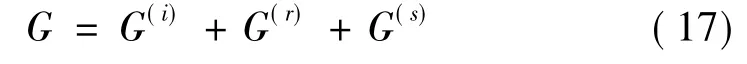
3 圆柱弹性夹杂对SH波的散射

对于SH波的入射问题，首先考虑直角平面区域内只含有圆柱夹杂时的情况.其求解思路与前面构造Green函数思路相同，将含圆孔的直角平面区域“镜像”为一个半无限空间对SH波的入射问题进行求解。因此，等效的入射波，反射波在复平面上的表达式为可以写成:

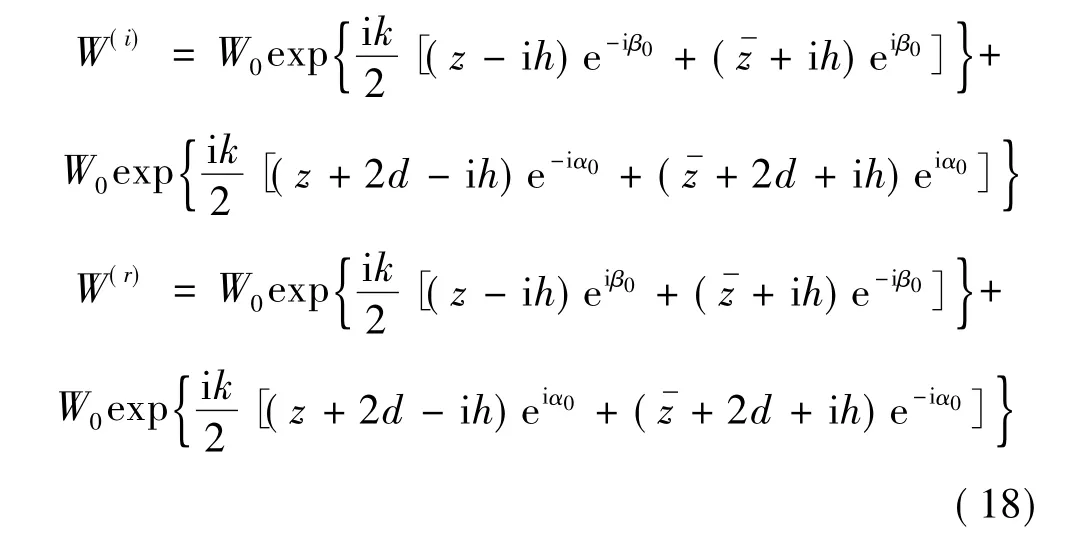
式中，β0=π－α0，α0为入射角，W0为入射波幅值。

SH波作用下由圆柱夹杂产生的散射波场及驻波场位移和应力表达式，与点源函数作用下圆柱夹杂产生的散射波场和驻波场的位移和应力表达式相同。其待定系数，由圆柱弹性夹杂边界的连续性条件确定，其解的过程与求解Green函数系数相同。

为了研究SH波对圆柱弹性夹杂的散射，首先，按裂纹“切割”技术构造裂纹，具体做法是:利用求得的Green函数，在欲出现裂纹处区域加置相应的大小相等、方向相反的平面荷载，使得此处应力为零，从而构造出裂纹。建立复平面此时圆柱夹杂与裂纹同时存在的直角平面区域内的波场为:

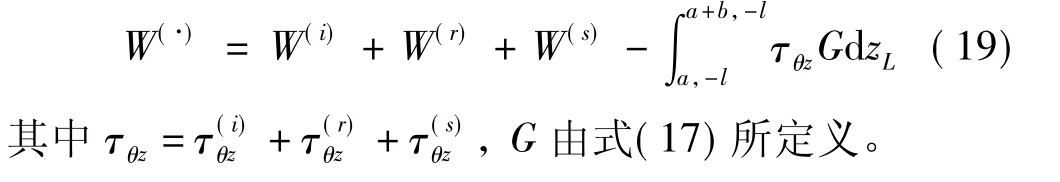
4 动应力集中系数(DSCF)

在稳态的入射SH波作用下，可以求出圆柱形弹性夹杂周边动应力分布，但求得动应力集中系数则是重要的任务之一。通常环向动应力集中系数可以写成:

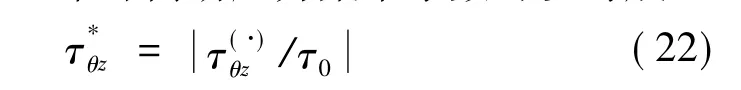
5 算例与分析

本文以花岗岩中含有混凝土夹杂为例，给出了SH波入射直角平面区域圆柱弹性夹杂时，其环向动应力集中系数的计算结果。其中花岗岩与混凝土的剪切模量之比 μ1/μ2=2.9，相应的波数之比为 k1/k2=0.667，夹杂位置的无量纲参数 d/R=12.0，h/R=12.0，夹杂半径 R=1.0;裂纹位置的无量纲参数为(a/R，l/R)，长度为b/R，倾斜角度为 β;无量纲入射波数用k1R表示，入射角度用α0表示。

(1)为了尽可能与已知结果进行比较，图4给出μ2=0.0这一极端情况下，SH波垂直入射时，圆柱夹杂动应力集中系数的分布情况，此时问题退化为圆孔问题，其结果与文献［11］一致。

(2)图5～图6给出了裂纹处于不同方位时，SH波分别以入射角度45°和90°入射时圆柱夹杂动应力集中系数的分布情况。由图中可以看出，当SH波入射方向与夹杂边界共线裂纹方向一致时几乎重合，此时裂纹的存在对的分布几乎没有影响，而当SH波入射方向与裂纹方向垂直时，对值的影响最大。当低频入射时，图形几乎对称于入射角度方向。由此也说明了入射角度对夹杂周边动应力集中系数的分布有一定的影响。

(3)图7给出不同裂纹长度且SH波垂直入射时圆柱夹杂动应力集中系数的分布情况。当b/R=0时，即介质中不含裂纹情况时，圆柱夹杂动应力集中系数左右对称，而当存在裂纹时的左右值不相等，且随着裂纹长度的增加，值增大。说明裂纹的长度也是影响值的因素。

(4)图8给出SH波垂直入射时圆柱夹杂边界点θ=0°处动应力集中系数随(－l/R)的变化情况。总体来说，当裂纹与边界点越近，DSCF值变化幅度越大。当SH波低频入射时最大值发生在( －l/R)=0处，最大值为5.72，比无裂纹状态时的值提高了12%，且当(－l/R)＞40时值几乎与无裂纹状态时的值重合，说明此时裂纹对边界点的影响几乎可以忽略不计。而当SH波以高频率入射时，最大值提高了14%，且当(－l/R)＞25时，裂纹对边界点值的影响可以忽略。

6 结论

本文利用复变函数及Green函数方法研究了含任意直线型裂纹的直角域中圆柱夹杂对SH波的散射问题，且与已有解答做了比较。总结算例，我们可以了解裂纹对的影响不可以忽略，尤其当裂纹距离夹杂较近时，夹杂边界点的值比无裂纹状态时的值提高了12% ～14%。当SH波低频入射且(－l/R)＞40时，裂纹对边界点的影响才可以忽略不计，而当SH波高频入射且(－l/R)＞25时，裂纹对边界点值的影响可以忽略。同时应用本文方法可以计算其他介质组合参数时的分布情况。

［1］王 铎，汪越胜.界面动力学研究近况［J］.上海力学，1993，14(4):1－15.

［2］王仁等.第十九届国际理论与应用力学大会(ICTAM)情况介绍［J］.力学与实践，1997，19(1):57－64.

［3］郑哲敏，周 恒，张涵信，等.21世纪初的力学发展趋势［J］.力学进展，1995，25(4):433－449.

［4］刘殿魁，刘宏伟.SH波散射与界面圆孔的动应力集中［J］.力学学报，1998，30(5):597－604.

［5］林 宏，刘殿魁.半无限空间中圆形孔洞周围SH波的散射［J］.地震工程与工程振动，2002，22(2):9－16.

［6］史守峡，刘殿魁.SH波与界面多圆孔的散射及动应力集中［J］.力学学报，2001，33(1):60－70.

［7］史文谱，陈瑞平，张春萍.直角平面内弹性圆夹杂对入射平面SH波的散射［J］.应用力学学报，2007，24(1):154－161.

［8］折 勇，齐 辉，杨在林.SH波对直角平面区域内圆形孔洞的散射与地震动［J］.应用力学学报，2008，25(3):392－398.

［9］李宏亮，刘殿魁.SH波作用下圆形夹杂与裂纹的相互作用［J］.哈尔滨工程大学学报，2004，25(5):618－623.

［10］杨在林，闫培雷，刘殿魁.SH波对浅埋弹性圆柱及裂纹的散射与地震动［J］.力学学报，2009，41(2):229－234.

［11］ Qi H，Shi Y，Liu D K.Interaction of a Circular Cavity and a Beeline Crack in Right-angle Plane Impacted by SH-wave［J］.Journal of Harbin Institute of Technology(New Series)，2009，16(4):548－553.

Scattering of SH-wave by a cylindrical Inclusion in right-angle plane with arbitrary beeline crack

QI Hui，YANG Jie，LI Hong-liang，YANG Zai-lin

(College of Aerospace and Civil Engineering，Harbin Engineering University，Harbin 150001，China)

Green’s function and complex function methods were used here to investigate the problem of scattering of SH-wave by a cylindrical inclusion in right-angle plane with an arbitrary beeline crack.Firstly，an essential solution to displacement field of an elastic right-angle plane containing a cylindrical inclusion while its any point bore a out-of-plane harmonic line source load was taken as Green's function.Secondly，crack was made out with crack-division technique，and expressions of displacement and stress fields were written during both crack and cylindrical inclusion exsiting.Finally，some examples and results for dynamic stress concentration factor of the cylindrical elastic inclusion were given，and the influence of crack on dynamic stress concentration factor at the edge of cylindrical elastic inclusion was discussed.

right-angle plane;cylindrical inclusion;arbitrary beeline crack;green's function;dynamic stress concentration factor(DSCF)

O343.1;P315.3

A

国家自然科学基金资助项目(10972064)

2009－12－21 修改稿收到日期:2010－03－10

齐 辉 男，教授，博士生导师，1963年生