水下航行器声学故障检测中距离有效性的评价

徐荣武，何 琳，汤智胤，崔立林

(海军工程大学 振动与噪声研究所，武汉 430033)

水下航行器声学故障检测中距离有效性的评价

徐荣武，何 琳，汤智胤，崔立林

(海军工程大学 振动与噪声研究所，武汉 430033)

引入J-偏差作为有向偏差的改进，并提出了一种新的距离有效性评价指标-归一化关键点高度(NKH)。利用仿真数据和舱段试验数据，以线谱频率改变等4种类型的常见声学故障为研究对象，针对欧氏距离等5种距离定义，系统地开展声学故障检测有效性的评价研究。结果表明，J-偏差的检测效果要优于常用的欧式距离和Hausdorff距离。

水下航行器;声学故障;距离检测

水下航行器在使用过程中不可避免的会出现振动噪声的异常，此种现象称为声学故障。对水下航行器的安静性状态进行监测和了解，及时发现和修复出现的声学故障，是水下航行器所面临的重要安全性问题。对于水下航行器，当机器或设备出现故障时，其振声信号特性一般会发生改变，因而通过实时监测水下航行器的振动和噪声信号，对声学故障进行检测识别，可以及时发现和消除水下航行器在使用过程中出现的声学故障，确保其隐身性能始终处于良好的状态［1，2］。

一种最常见的在线检测思路是在水下航行器运行工况保持不变的前提下，首先计算当前振动噪声状况的频谱特征，然后将当前特征与前一时刻进行比较，一旦两者之间的距离超过某一预设阈值，则作出声学故障检测结果为真的判决［3，4］。不难看出，如何准确合理地给出频谱间距离的定义，对于提高声学故障检测结果的置信度，降低误报率具有非常重要的作用。

因此，本文利用仿真数据和舱段试验数据，以线谱频率改变等4种类型的常见声学故障为研究对象，针对欧氏距离等5种定义，系统地开展检测有效性的评价研究。

1 研究对象与度量指标

1.1 声学故障的类型

水下航行器辐射噪声的三个主要来源是机械噪声、螺旋桨噪声和水动力噪声［5］。而且在低航速时，机械噪声往往成为主要噪声源。在一般情况下，辐射噪声由宽带连续谱和一系列线谱组成。其中线谱成分与推进系统，螺旋桨及辅机有关。辅机产生的线谱分量通常是稳定的，且这类线谱的频率与航速无关。推进系统和螺旋桨产生的线谱的幅度和频率随着航速变化而变化，且有周期性的调制现象。因此在声学故障的研究中需要同时关注宽带噪声与线谱特征。一般地，声学故障通常可分为以下4种主要类型［3］:

类型(1)——线谱频率改变:原频谱中某线谱的频率发生明显变化，且变化范围超过某一预设阈值。

类型(2)——新线谱的出现:在原频谱中出现了明显的新线谱。

类型(3)——窄带功率增加:原频谱中某线谱的功率或振幅的增加量大于某一容许的阈值。

类型(4)——宽带功率增加:原频谱中整个频谱的总功率增加量大于某一容许的阈值。

1.2 研究对象概述

本文以如下5种不同的距离度量标准作为研究对象:欧氏距离 (Euclidean distance)［6］、频谱角 (Spectral angle)［7］、J- 偏差 (J-divergence)［8］、总功率差(Diference in total power)［9］和 Hausdorff距离 (Hausdorff distance)［10］。

1.2.1 欧氏距离

假定研究对象为两个包括n个不同频段的频谱P和Q，且频谱P的第i个频段功率大小表示为P(i)，频谱Q的第i个频段功率大小表示为Q(i)。则频谱P和Q间的欧氏距离可表示为:

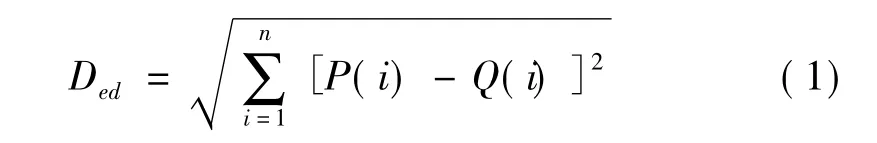
1.2.2 频谱角

1.2.3 J- 偏差

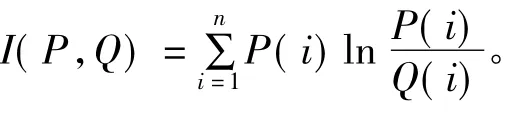
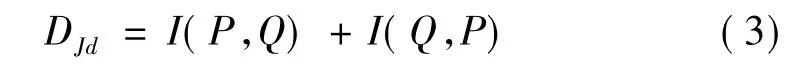
1.2.4 总功率差

总功率差的计算公式为:

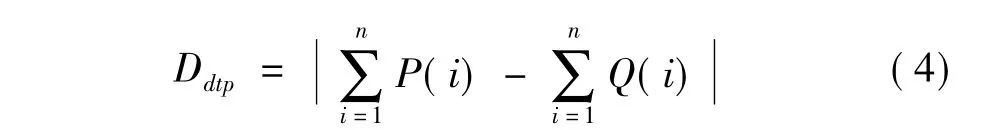
1.2.5 Hausdorff距离

Hausdorff距离是描述两组点集之间相似程度的一种量度，它是集合与集合之间距离的一种定义形式。对于 P、Q 两组频谱，不妨设 P={P1，P2，…，Pm} ，Q={Q1，Q2，…，Qn} 。则这两组点集之间的 Hausdorff距离可以定义为:

1.3 评价指标

现有研究中一般都是通过人工主观判断来对不同距离度量的性能差异进行评价［12］，因此评价结果往往不够客观和稳定。文献［3］提出采用归一化峰高(Normalized Peak Height，NPH)作为评价指标，其定义为相邻频谱间距离的最高峰值除以相邻频谱间距离的标准偏差。但其缺点在于:(1)由于未对峰值位置进行预判断，因此当信号信噪比过低时，所求得的最高峰位置(即理论上声学状态的变化点)可能与实际上声学状态发生变化的时刻并不一致(图1);(2)没有考虑距离序列的平均水平对检测性能的影响。即当最高峰值相同时，距离序列的平均水平值越低，检测效果就应当越好。

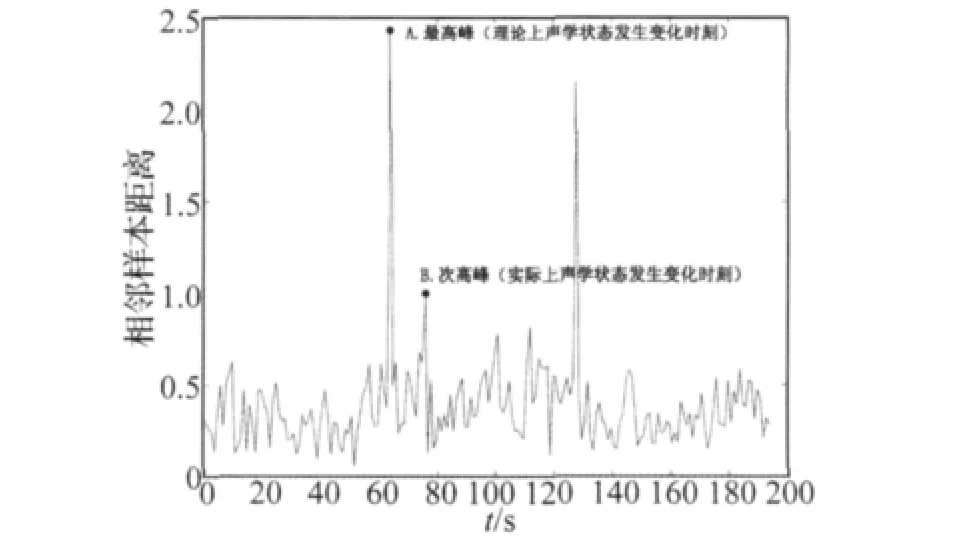
图1 声学状态的变化点的不一致Fig.1 Unmatching between the change points in theory and practise

因此，基于上述讨论，本文提出了一种新的量化的评价指标，称为归一化关键点高度(Normalized Keypoints Height，NKH)。设相邻频谱间距离序列为S，且S中全体关键点(即声学状态变化时刻)的索引为INDkp，(S-SINDkp)表示S中剔除全部关键点后的子集，则NKH定义如下:

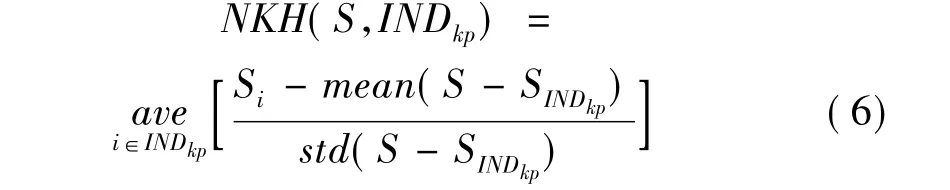
从公式(6)中不难看出，NKH的实质是全体关键点进行归一化后的算术平均值。当关键点峰值越高、剩余序列的平均值越低且变化越平稳时，距离序列的NKH值就越大，表示检测性能就越好。

2 仿真试验

［3］中的作法，本文同样利用仿真试验为了研究信噪比对距离度量标准的影响。以第(2)类声学故障(新线谱的出现)作为研究对象。仿真数据可分为等长度的3个数据段，其中数据段1和数据段3为白噪声信号，而数据段2为白噪声信号叠加线谱，用以模拟声学状态“正常—故障—正常”的变化过程，其详细描述如表1所示。

显然，表1中仿真数据对应的相邻样本距离序列总长度为192，其中关键点有2个，对应序列索引为64和128，分别对应线谱的出现时刻和消失时刻。试验数据分为10组，信噪比(SNR)分别为 -2 dB、-4 dB、-6 dB、-8 dB、-10 dB、-12 dB、-14 dB、-16 dB、-18 dB和-20 dB。为降低随机因素的影响，每组试验均重复15次。

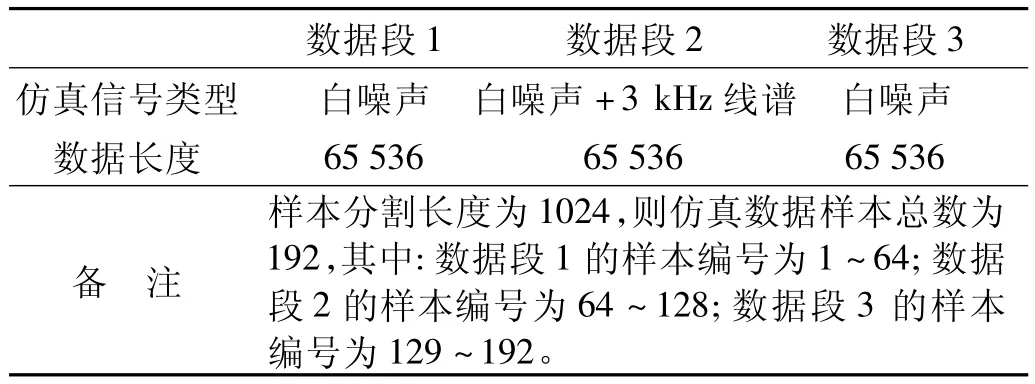
表1 数据段的描述Tab.1 Description of test data

试验结果表明(表2)，当SNR＞-12 dB时，欧氏距离、频谱角和 J-偏差均能顺利地检测出2个关键点;而当SNR≤-12 dB时，由于关键点已完全淹没在噪声信号中，此时5种距离度量都已无法准确对声学故障作出检测。

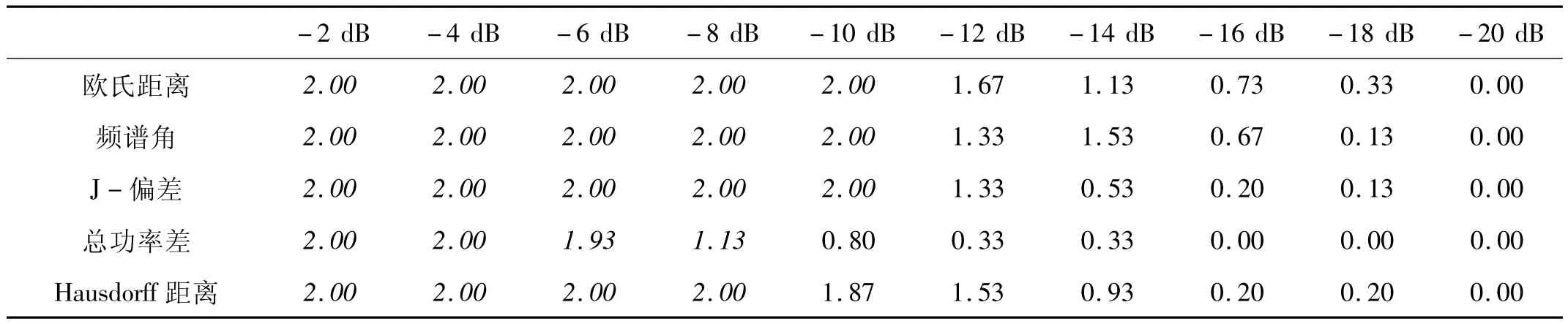
表2 不同信噪比条件下关键点个数检测结果(15次试验平均值)Tab.2 The number of key points under different SNR(15 times averaging)

因此，仅以欧氏距离、频谱角和 J-偏差作为进一步研究对象，分别计算其在SNR＞-12时的 NKH值，结果如表3所示:

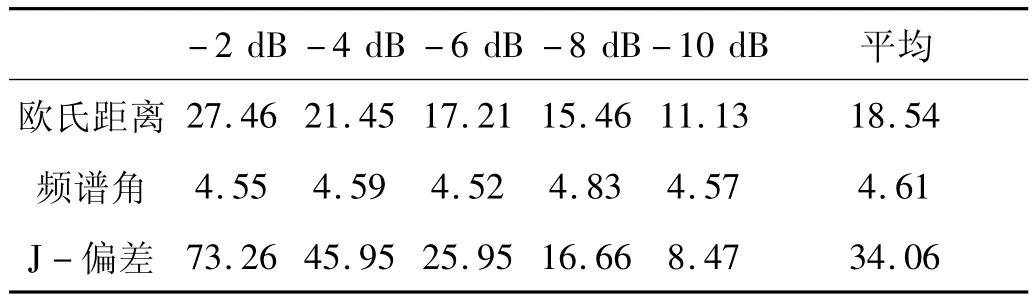
表3 各种信噪比条件下不同距离度量的NKH比较Tab.3 The NKH value under different SNR

从表3中不难看出，J-偏差效果最佳，其平均NKH值分别是欧氏距离和频谱角的1.84倍和7.39倍。

3 舱段模型试验

在仿真试验的基础上，进一步选择选择某水下航行器舱段模型作为试验对象。在模型内部布置电机(图2)、激振机(图3)和海水泵(图4)各一台，通过设备不同工况的组合来模拟不同类型的噪声源状态。

试验测试系统如下:信号发生器—B＆K 1049;功率放大器—B＆K2707;激振机—B＆K 4801T;信号采集系统—B＆K 3560D+PULSE 8.0;加速度传感器—PCB 352C33 ICP型加速度计。系统采样频率为800×2.56=2 048 Hz，采样时间为8 s。加速度传感器布置于舱段模型外壳左舷。

类似上节中的做法，每类声学故障数据仍然分为3个数据段，用以表示“正常—故障—正常”的全过程，具体设置如表4所示。

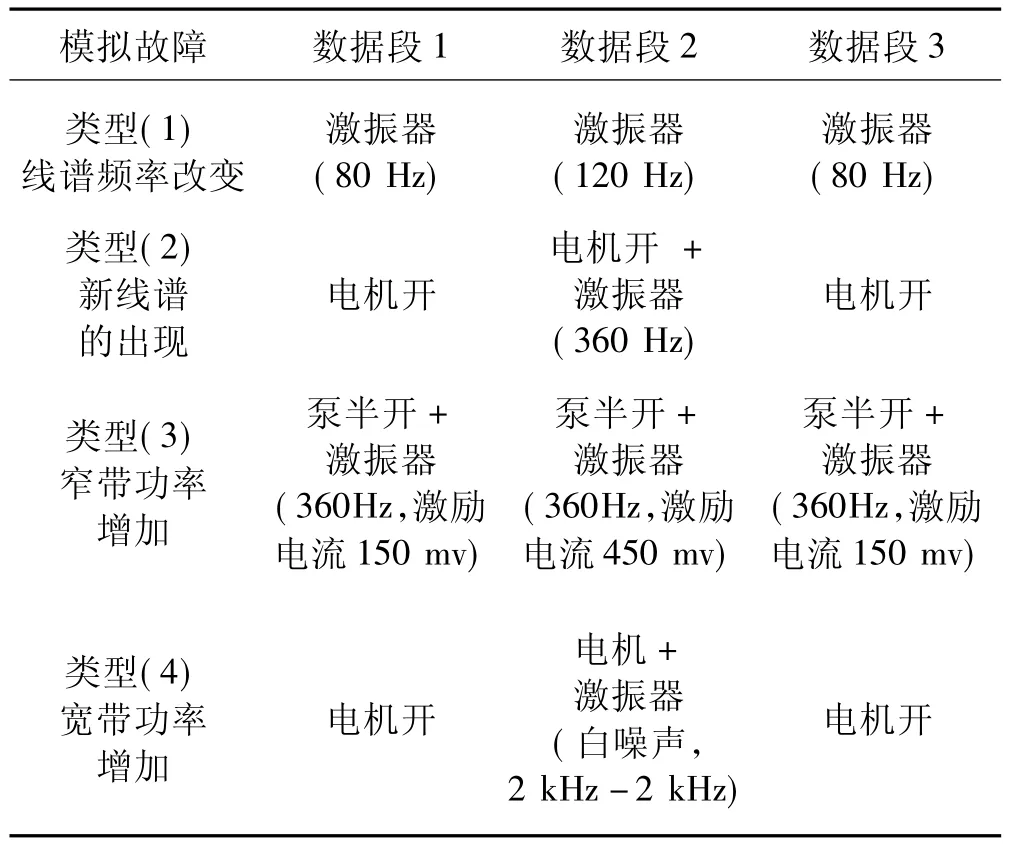
表4 声学故障工况设置Tab.4 List of acoustic fault conditions

此外，为更好的模拟水下航行器的实际工作环境，本文在每类工况的数据中人工叠加白噪声(SNR=-5 dB)。试验的主要结果如表5和表6所示。

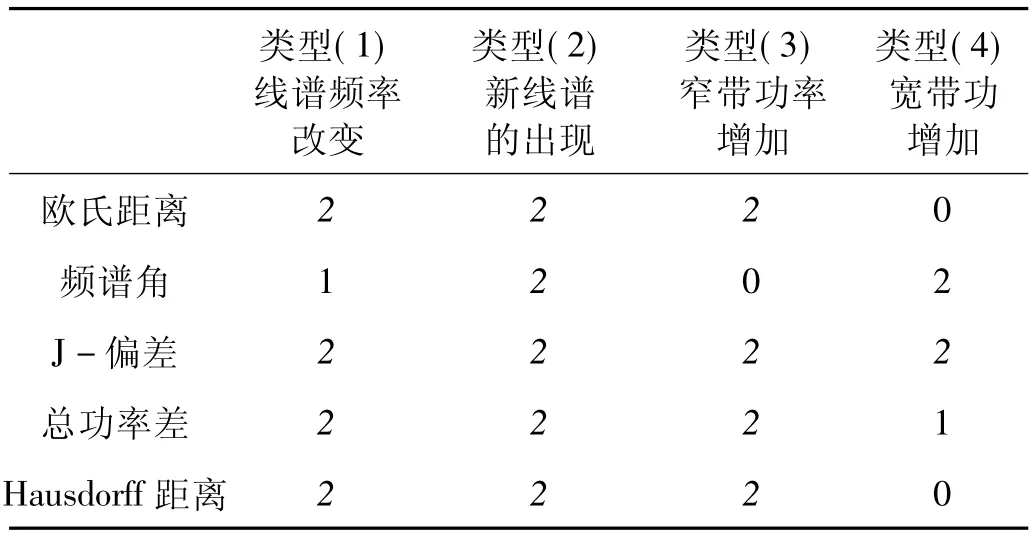
表5 不同声学故障设置下关键点个数检测结果(15次试验平均值)Tab.5 The number of key points when setting different acoustic faults(15 times averaging)

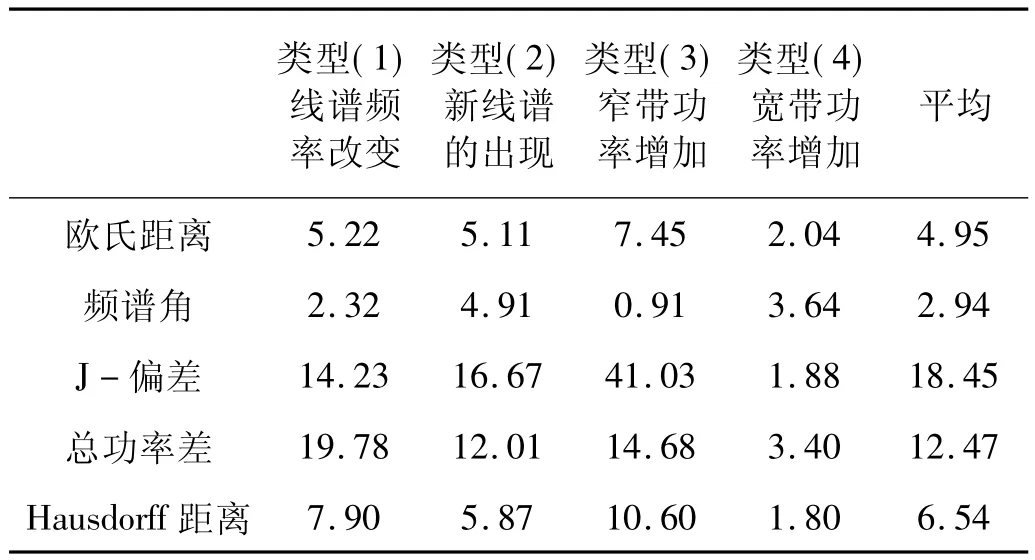
表6 各种信噪比条件下不同距离度量的NKH比较Tab.6 The NKH value when setting different acoustic faults

因此，从关键点检测效果和 NKH值两个方面看，J-偏差都要由于其他距离定义。这也验证了第2节仿真试验中的结论。

4 结论

本文引入J-偏差作为有向偏差的改进，提出了一种新的距离有效性评价指标—归一化关键点高度(NKH)。利用仿真数据和舱段试验数据，以线谱频率改变等4种类型的常见声学故障为研究对象，针对欧氏距离等5种定义，系统地开展检测有效性的评价研究。结果表明:

(1)归一化关键点高度(NKH)与实际检测结果具有很好的一致性，可以较好地刻划不同距离度量的有效性能。

(2)与常用的距离定义如欧氏距离［3］和Hausdorff距离［12］相比，J-偏差能够灵敏地反应出传感器频谱特征中线谱频率改变、新线谱的出现、窄带功率增加和宽带功率增加等水下航行器声学状态的变化，同时具有较好的抗噪性能，适合工程应用。

参考文献

［1］Eatwell G P，Dorling C M.Practical Techniques For Noise Path Identafication.Underwater Defence Technology.In:UDT;1990.

［2］周军伟，朱海潮，章林柯.基于KNN分类算法的水下航行器声学故障检测识别研究［J］.噪声与振动控制，2009，29(2):59-62.

［3］O'Mara D，Gear G，McMahon D R.Automated self-noise monitoring and acoustic fault detection.In:UDT;2002.

［4］ Yamanishi K， Takeuchi J-i， Williams G. On-line Unsupervised Outlier Detection Using Finite Mixtures with Discounting Learning Algorithm［J］.Data Miningand Knowledge Discovery，2004，8(3):275-300.

［5］ Urick R J. PrincipalsofUnderwaterSound: McGraw Hill;1983.

［6］Waner S，Levine G C.Introduction to Differential Geometry and General Relativity:Departments of Mathematics and Physics，Hofstra University;1989.

［7］Ciminello M，Szlyk T.The Classification of Terrestrial Materials and Vegetation Using Remotely Sensed Multi-Spectral Data at the AUTEC's Main Base on Andros Island，Bahamas.In:UDT;2004.

［8］Lin J.Divergence Measures Based on the Shannon Entropy［J］.Ieee Transactions on Information Theory，1991，37(1):145-151.

［9］肖邵予，汪 浩，吴英友，等.统计学在结构噪声监测中的运用［J］.中国舰船研究，2008，3(4):45-49.

［10］ Hemminger T L.A real-time neural-net computing approach to the detection and classification of underwater acoustics transients:Western Reserve University;1992.

［11］ Kullback S.Information Theory and Statistics.New York:Dover Publications;1968.

［12］ Aiordãchioaie D，Dugan V.Metrics for Spectral Amplitude Classification.In:Proceedings of the 5th European Congress on IntelligentTechniques and SoftComputing; 1997;Aachen，Germany，1997，1784-1788.

Detection of underwater vehicle's acoustic fault

XU Rong-wu，HE Lin，TANG Zhi-yin，CUI Li-lin

(Naval University of Engineering，Wuhan 430033，China)

J-divergence was induced as an improvement of directive divergence.By introducing a new kind of evaluation index，normalized key-points height(NKH)，a simulation and a cabin model test were presented to evaluate the effect of five different distance concepts including Euclidean distance etc.on four kinds of acoustic faults.The result showed that J-divergence is the best choice for acoustic fault detection.

underwater vehicle;acoustic fault;distance-based detection

TB533;U674

A

国家自然科学基金(50775218)

2010-01-15

徐荣武 男，博士，讲师，1980年3月生