基于混合PSO算法的桁架动力响应优化
魏徳敏,文星宇
(1.华南理工大学 土木工程系,广州 510640;2.华南理工大学 亚热带建筑科学国家重点实验室,广州 510640)
基于混合PSO算法的桁架动力响应优化
魏徳敏1,2,文星宇1
(1.华南理工大学 土木工程系,广州 510640;2.华南理工大学 亚热带建筑科学国家重点实验室,广州 510640)
针对以结构动力响应为约束,最小重量为目标的桁架拓扑优化问题,提出了一种将微粒群算法和优化准则法结合的混合PSO算法。利用优化准则法的迭代关系找出群体中适应度最好的微粒,将其作为特殊微粒,其他微粒的寻优采用PSO的基本进化规则,位移响应约束利用特殊微粒的灵敏度信息近似计算。算例的计算结果表明,混合PSO算法适用于受简谐荷载以及脉冲荷载作用桁架结构的拓扑优化。混合PSO的计算效率比PSO算法高,其优化效果比优化准则法好。
混合PSO;动力响应优化;拓扑优化;位移响应约束
结构优化研究包含有静力优化、动力特性优化以及动力响应优化等。由于动力响应优化同时涉及到结构动力响应分析和优化设计,因此求解更为复杂,目前已有的研究成果相对也较少。潘晋[1]采用自适应遗传算法求解了脉冲激励下的桁架结构拓扑优化问题。Rong[2]提出了适合动力拓扑优化问题的 ESO方法。Ma等[3]采用改进优化准则法求解连续结构动力拓扑优化问题。Choi等[4]提出了一种新型拟静力方法,将动力优化问题转换为多工况静力优化问题,可以弥补传统拟静力法的不足,但计算量较大。
本文针对动力位移响应约束下的桁架结构拓扑优化问题,提出了一种将微粒群算法(PSO)和优化准则法相结合的混合算法。这种混合算法用优化准则法的迭代关系找出群体中适应度最好的微粒作为特殊微粒,其他微粒的寻优采用PSO的基本进化规则,然后利用特殊微粒的灵敏度信息近似计算自身的位移响应约束。通过算例分析发现,该方法能够利用动力响应灵敏度信息,大幅提高PSO的寻优效率,概念简单,易于实现。适用于受脉冲荷载作用的桁架结构优化分析。
1 动力响应优化问题的数学模型
典型桁架结构优化问题是在满足动力响应约束的情况下求解最轻重量,其数学模型为:

式中,n为杆件数,m为所考虑的约束个数,Lj和xj分别为杆件j的长度与横截面积,xd和xu为杆件横截面积的下限和上限,gi为第i个动力响应约束,一般为时间和设计变量的复合隐式函数。本文将结构关键部位的位移幅值作为约束,即:

式中,zi为第i个控制部位上任意时刻的位移值为位移限值。为了便于计算该约束的灵敏度信息,通常将其转变为一个时间段上的积分型约束:

不难看出,若式(3)满足,式(2)自然满足,反之亦然。但需要强调的是,式(2)和式(3)这两种约束形式并不存在严格意义上的等效关系[5]。由于积分型位移响应约束不依赖一个具体的时间,故便于计算灵敏度信息。
2 优化方法
2.1 PSO算法
PSO是一种新型智能搜索优化算法,能够利用群体智能性来求解复杂的优化问题,适用于结构静力与动力特性优化问题[6,7]。
PSO中的微粒对应于搜索空间中的点,假设搜索空间的维数为n,种群的规模为M,第r个微粒的位置xr和速度vr可表示为:
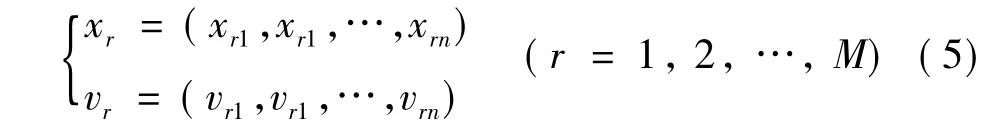
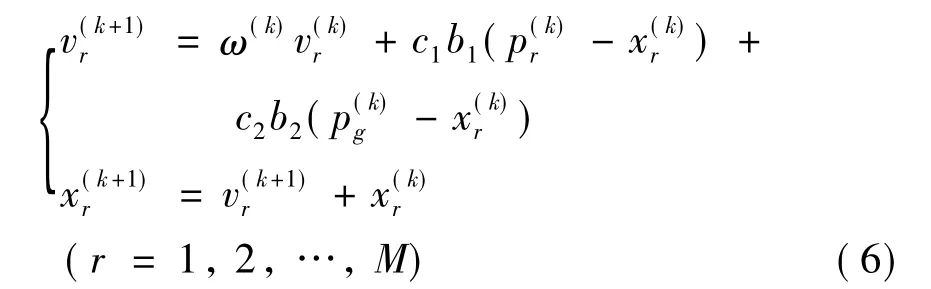
式中,pr和pg分别表示第r个微粒个体历经的最优位置和所在群体历经的最优位置,系数ω为惯性权重,c1和c2为加速常数,b1和b2为在0和1之间均匀分布的随机数。若限制微粒的最大速度,则有:
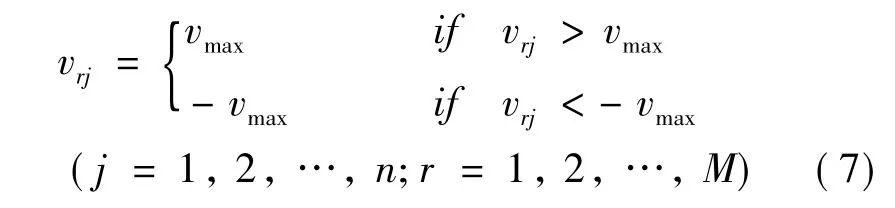
微粒的优劣程度可由以下适应度函数判断:
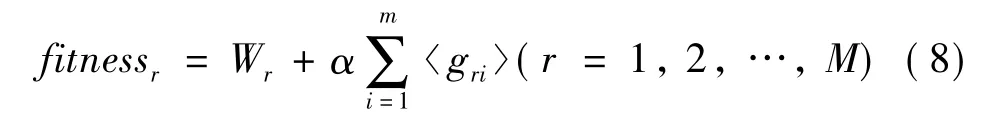
式中,Wr为微粒r的目标函数,gri为微粒r的第i个约束值,α为罚因子。
2.2 优化准则法
在优化准则法中,一般只需进行简单的迭代求解,因此计算效率较高。本文将文献[3]和文献[8]中的设计变量迭代列式加以改进,使其适用于任意多个约束的动力响应优化问题。其形式为:
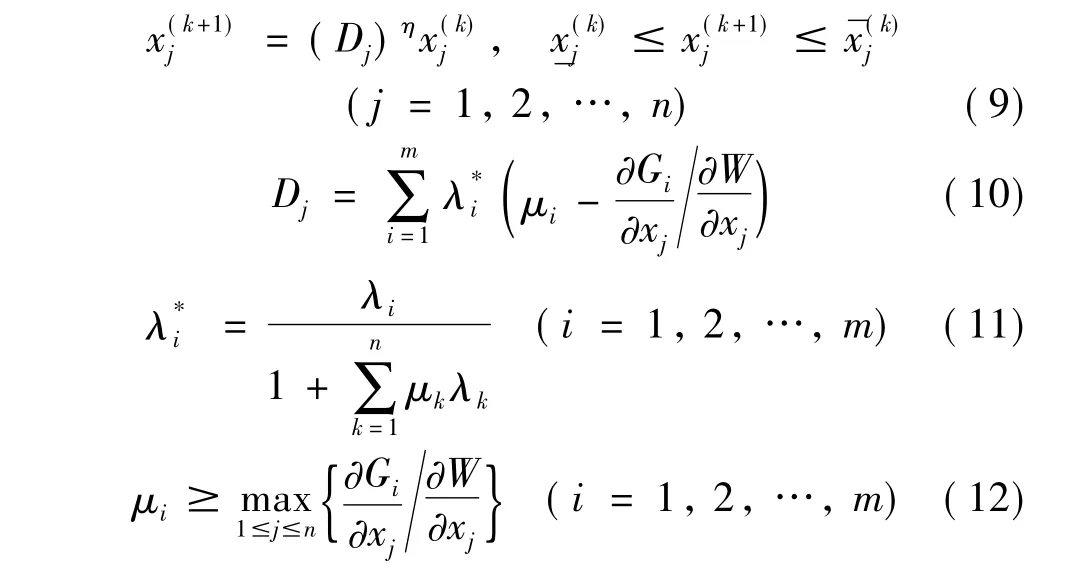
式中,W为目标函数,Gi为第i个约束和分别为杆
件横截面积变量的运动上限和下限。参数λi为第i个约束对应的拉格朗日乘子。参数η一般取为0.1~0.5,η取较大的值可加快寻优速度,但在迭代后期会引起目标函数值的震荡,而η取值较小计算平稳,但迭代次数较多。
估算拉格朗日乘子λi是优化准则法中的关键步骤,本文经过计算分析发现,对式(3)所示积分型位移约束,可使用一种简单的估算公式,以下给出具体实施方法。
首先对积分型约束进行一定程度的放松处理,将约束gi的形式变为:

需要注意的是,若满足式(2)或式(13),则式(14)自然满足,但式(14)成立并不能保证式(2)或式(13)也严格成立,所以放松型积分约束可能使位移响应超出限值,需要通过调节参数ξ控制误差。
重量最轻优化问题的拉格朗日乘子估算式即为:
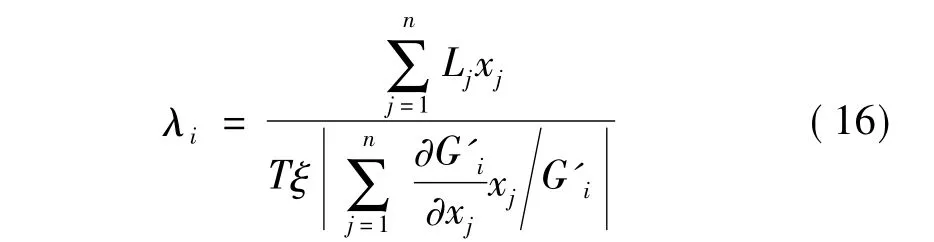
式(10)和式(16)中积分型约束的灵敏度可用伴随变量法计算,具体求解过程详见参考文献[5]。
2.3 混合PSO算法
基本PSO没有利用灵敏度信息,而需是进行大量的结构动力分析,故效率较低。而优化准则法对于复杂约束的情况,难以得到全局最优解。考虑到两种优化方法都是执行单一迭代格式,因此本文将它们结合成一种混合算法,从而弥补了原方法各自的缺陷。
混合PSO的基本思想是将式(9)看成微粒的另一种进化规则,由于它属于敏度类算法,其寻优效率较高,因此只需个别微粒采用这种新进化规则,即可提高整个群体的寻优效率。另外,利用特殊微粒的灵敏度信息,近似计算其他微粒的动力响应[9],也可有效减少计算量。
若特殊微粒为xs,其动力响应约束为Gs,则其他微粒的动力响应约束采用线性近似计算,即:

线性近似的精度和微粒间距xr-xs有关,为确保误差可控,Δx的取值不宜过大。一般前期微粒之间的差异较明显,可采用较松的运动极限,后期微粒逐渐趋于一致,则必须收紧运动极限。
混合PSO算法的具体实施步骤如下:
① 随机生成特殊微粒 xs,并计算运动极限和。
③ 计算特殊微粒的动力响应约束、灵敏度以及适应度,特殊微粒按式(9)运行①步。
④ 其余微粒按式(6)运行p步,用式(17)估算位移响应约束,并计算适应度。
⑤ 选择适应度最好的微粒作为新的特殊微粒,并更新相应的运动极限和。
⑦ 检查是否满足停止条件,若不满足则返回到步骤③。
上述所有微粒的适应度按下式计算:
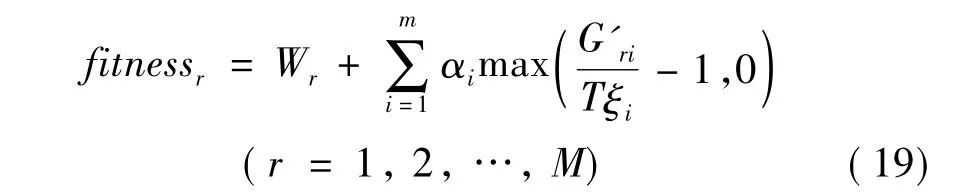
步骤⑦中停止条件有多种选择,可由特殊微粒的最大迭代次数决定,也可由目标函数停止更新的循环次数决定。与基本PSO算法相比,混合PSO算法的微粒规模M以及运行次数p可取为较小的值。
不难看出,混合PSO采用了放松型积分约束,因此并不严格满足约束条件,而且近似动力响应分析有可能使位移响应超限,需要通过收紧运动极限加以改善。另外,由于混合PSO不是在整个设计域中搜索,且受灵敏度信息的影响,故找到全局最优解的几率可能比基本PSO要小。然而,若有全部特殊微粒的动力响应和灵敏度记录,就能扩大适合近似分析的区域,提高全局搜索能力。
3 算例分析
本文算例均以动力位移响应为约束,以结构最小重量为优化目标,用基本PSO、优化准则法以及混合PSO分别进行结构拓扑优化设计,然后对三种算法的计算结果和耗时情况进行对比分析。
3.1 简谐荷载作用下十二杆桁架优化
十二杆平面桁架如图1所示。所有杆件的初始截面随机取值,材料密度ρ=2 715.07 kg/m3,弹性模量E=6.9 ×106N/cm2,结构各阶模态阻尼比 ξ=0.03。考虑两个静荷载工况,工况Ⅰ:P2y=-4.45×105N;工况Ⅱ:P4y=-4.45×105N;在两种工况下,结点2作用竖向简谐动载F=-40cos(50 t)kN。杆件允许应力[σ]=17 243.5 N/cm2。位移约束为结点2,4在y方向上的位移不超过5.08 cm。
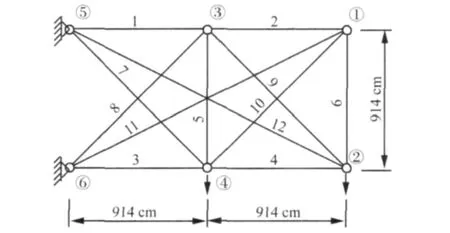
图1 平面十二杆桁架Fig.1 12-bar plane truss
选取优化准则法的参数为:η=0.2,Δx由5线性减小到3,迭代次数为100。基本PSO中的参数为:群体规模为30,进化次数为200,加速常数c1=c2=2.0,ω采用线性下降方案,初始 ωmax=1.1,下限 ωmin=0.3,微粒速度上限vmax=5,适应度函数中罚因子α=105。混合PSO法中参数为:η=0.2,Δx由5线性减小到1;群体规模为30,特殊微粒最大迭代100次,普通微粒在一次循环中运行次数p=40;加速常数c1=c2=1.2,ω=0.5。三种算法的结构动力分析均采用Newmark法,积分步长为结构最小周期的十分之一,分析时长为一个基本周期。
优化后的桁架拓扑构形如图2所示。优化后的杆件截面积以及其他结果见表1和表2。
由表1和表2可知,即使存在多工况和复杂的静动力约束,三种优化算法都有较好的效果,但计算结果有一定的差异。准则法的优化效果比其他两种方法差一些,原因可能是多约束情况下拉格朗日乘子估算精度不够;PSO的优化解较理想,,并且严格满足所有的约束条件。综合比较后,可知混合PSO的优化解是最好的,得到的结构重量最轻,只是位移约束稍有超限。
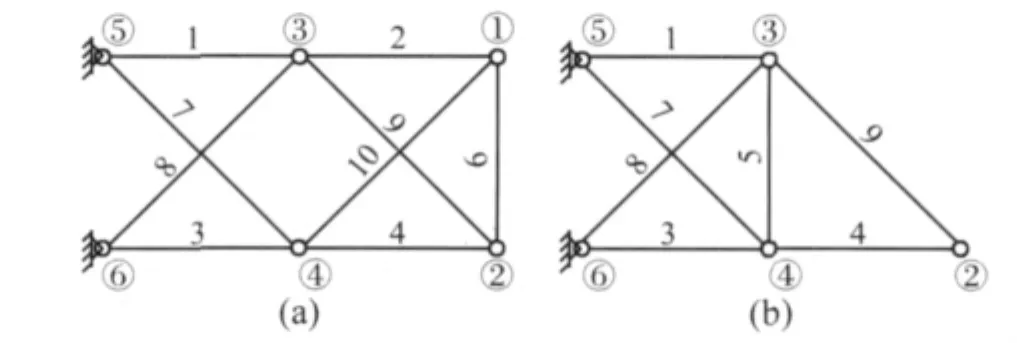
图2 十二杆桁架最优拓扑Fig.2 Optimum topology of the 12-bar plane truss

表1 优化后的杆件横截面积(单位:cm2)Tab.1 Cross-sectional areas of Optimized bars(Unit:cm2)
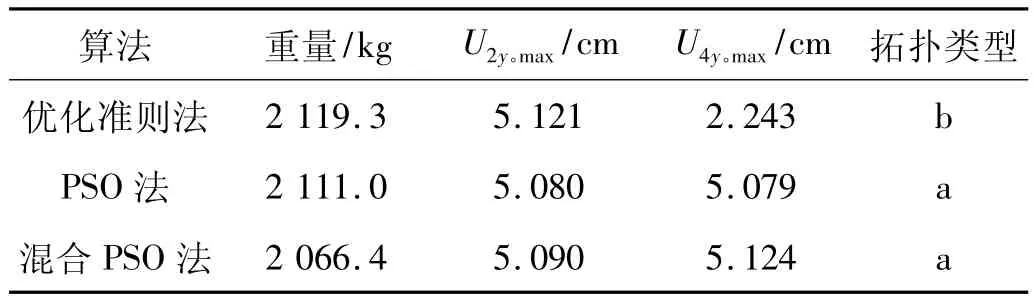
表2 三种算法的优化结果对比Tab.2 Comparison of the three optimization results
虽然三种优化算法所得最优截面积并不相同,最优拓扑构形也不完全一致,但这都是比较正常的现象。
因为简谐荷载作用的结构动力响应优化问题是典型的设计域分离问题,三种优化算法都只能获得局部最优解。
3.2 脉冲荷载作用下二十杆桁架优化
该平面桁架的基结构如图3所示,杆件横截面分组情况见表3。杆件初始横截面积随机取值,杆件的弹性模量、密度以及模态阻尼比与上例相同。在桁架节点6作用一竖向矩形脉冲荷载P=4.45×105N,荷载作用时间为0.008 s。规定节点6的竖向振幅不超过4 cm。结构动力分析采用Newmark法,积分步长为结构最小周期的十分之一,分析时长为一个基本周期。
PSO算法的参数选取为:群体规模M=30,进化次数N=400,加速常数c1=c2=2.0,惯性权重ω采用线性下降方案,初始 ωmax=1.1,下限 ωmin=0.3,微粒速度上限vmax=5,罚因子α=105。优化计算10次,取其最好的结果。
优化准则法的参数选取为:η =0.1,ξ=0.1,T=0.2,迭代最大次数为 100。
混合PSO的参数选取为:群体规模M=20,每一次循环微粒运行次数p=40,加速常数c1=c2=1.8,ω≡0.5,速度上限 vmax=3。式(17)中 Δx初始时取5,再线性变化到1。其余参数 η =0.1,ξ=0.1,T=0.2,特殊微粒最大迭代次数为80。优化计算10次,取其最好的结果。
桁架最优拓扑如图4所示,三种算法的优化过程如图5所示,优化前后的杆件截面积以及结构特性的比较见表3和表4。
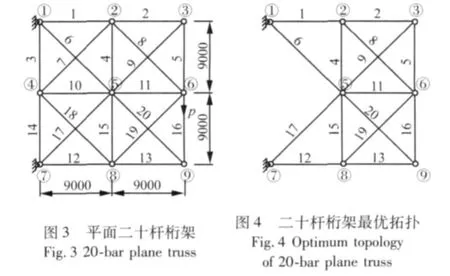

表3 优化后的杆件横截面积(单位:cm2)Tab.3 Cross-sectional areas of Optimized bars(Unit:cm2)
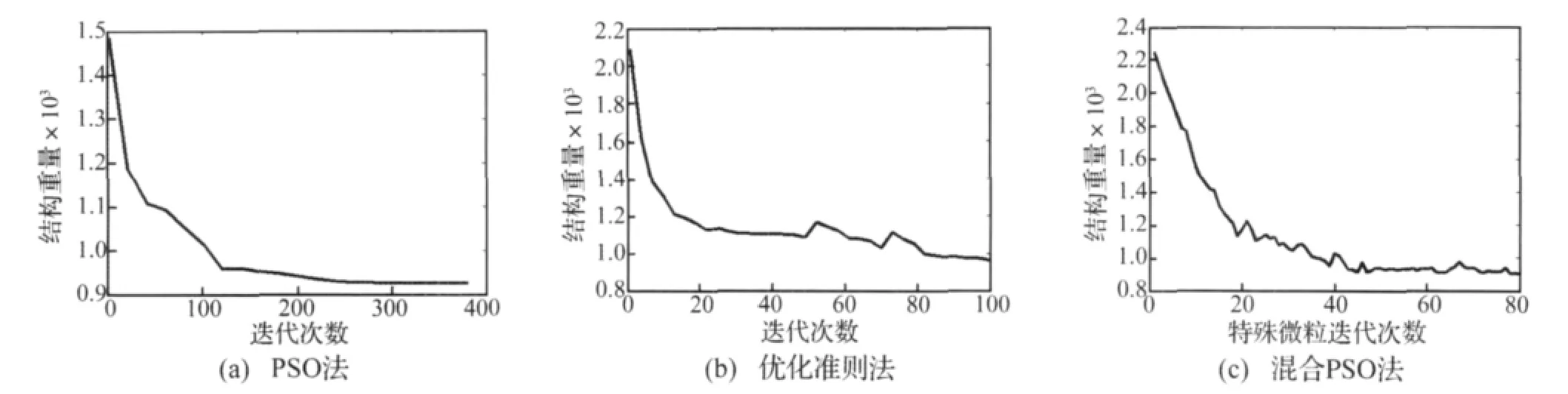
图5 结构重量优化过程Fig.5 Optimization process for the structural weight
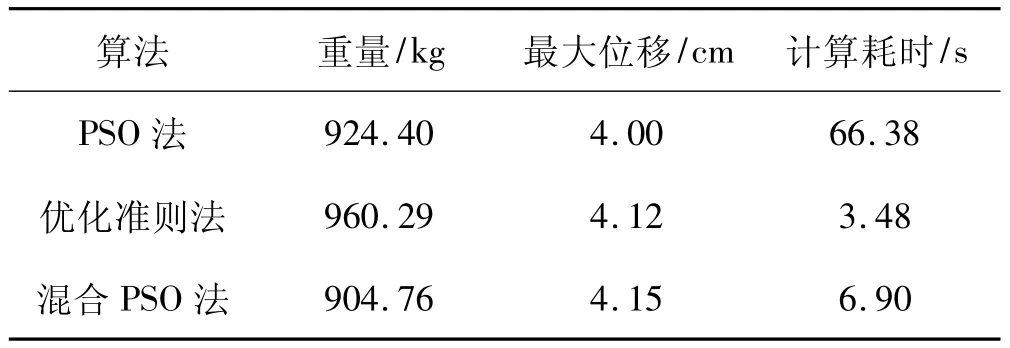
表4 三种算法的优化结果对比Tab.4 Comparison of the three optimization results
通过计算分析可知,以上三种优化算法都可以得到桁架的最优拓扑构型,但它们的结果有一定的差异。由表4可以看出,基本PSO的优化效果最好,能够严格满足动力位移约束,但计算耗时远远超过其他两种方法,因此不便于实际工程应用。优化准则法计算效率最高,但未得到最优解,且动力位移约束不能严格满足。混合PSO的优化效果好于优化准则法,计算耗时远少于基本PSO算法。
综上所述,本文提出的混合PSO保留了基本PSO算法和优化准则法二者的优点,优化过程较为简单高效,比较适用于计算规模较大的结构优化问题。关于混合PSO算法还有一些需要进一步研究的问题,譬如其他精度更高、计算量不大的近似分析方法,针对积分型位移响应约束提出的拉格朗日乘子简单估算式(16)的改进,目标函数值的稳定收敛性,参数的合理选择及其对算法性能的影响等。
[1]潘 晋,王德禹.动力响应约束下的桁架结构拓扑优化[J].振动与冲击,2006,25(4):8-12.
[2] Rong J H.Topology optimization of structures under dynamic response constraints[J].Journal of Sound and Vibration,2000,243(2):177-189.
[3]Ma Z D,Kikuchi N,Cheng H C.Topological design for vibrating structures[J].Computer Methods in Applied Mechanics and Engineering,1995,121:259-280.
[4] Choi W S,Park G J.Structural optimization using equivalent static loads at all time intervals[J].Computer Methods in Applied Mechanics and Engineering,2002,191:2077-2094.
[5] Kang B S,Park G J,Arora J.A review of optimization of structures subjected to transient loads[J].structure multidisciplinary optimization,2006,31:81-95.
[6]袁代林,陈 虬.桁架结构拓扑优化的微粒群算法[J].西南交通大学学报,2007,42(1):94-98.
[7]孙木楠,史志俊.基于粒子群优化算法的结构模型修改[J].振动工程学报,2004,17(3):350-353.
[8] Venkayya V B.Optimality criteria:a basis for multidisciplinary design optimization[J].Computational Mechanics,1989,5:1-21.
[9] Salajegheh E.Structural optimization using response approximation and optimality criteria methods[J].Engineering Structures,1997,19(7):527-532.
Dynamic response optimization for a truss structure based on hybrid PSO algorithm
WEI De-min1,2,WEN Xing-yu1
(1.Department of Civil Engineering,South China University of Technology,Guangzhou 510640,China;2.State Key Laboratory of Subtropical Building Science,South China University of Technology,Guangzhou 510640,China)
A hybrid algorithm was proposed for dynamic topology optimization of a truss structure.In optimization analyses the dynamic displacement responses of nodes were constrainted and the minimum weight of the truss structure was taken as the objective function.A particle having the best fitness from a swarm was chosen as the special particle,and it moved by means of iteration expressions in the optimality criterion method.The other particles complied with the evolution rules of PSO algorithm,and their displacement constraints were approximately calculated by using the dynamic sensitivity of the special particle.The optimization results of an example showed that the hybrid PSO algorithm is suitable for the topology optimization of the truss structure under the harmonic load and impulsive load;the optimization efficiency of hybrid PSO algorithm is higher than PSO algorithm,and the optimization precision of hybrid PSO algorithm is better than that of the optimality criterion method.
hybrid PSO algorithm; dynamic response optimization; topology optimization; displacement response constraint
O189
A
2009-09-21 修改稿收到日期:2010-03-23
魏徳敏 女,博士,教授,1955年生

