飞机T型尾翼颤振计算的若干关键问题
杨 飞, 杨智春
(1.中国商飞上海飞机设计研究院 强度部,上海 200232;2.西北工业大学 航空学院,西安 710072)
飞机T型尾翼颤振计算的若干关键问题
杨 飞1, 杨智春2
(1.中国商飞上海飞机设计研究院 强度部,上海 200232;2.西北工业大学 航空学院,西安 710072)
由于飞机T型尾翼的结构与气动布局特点,T型尾翼颤振计算不能套用常规尾翼的分析方法,而需要考虑平尾面内运动以及静升力等因素的影响。从T型尾翼的工程颤振分析出发,讨论了T型尾翼颤振计算中的若干关键问题,阐述了T型尾翼颤振特性的特点和影响T型尾翼颤振特性的关键参数,分别介绍了现有的几种T型尾翼颤振计算中的气动力修正方法,提出了T型尾翼颤振工程计算中必须注意的问题。
T型尾翼;颤振;气动力;偶极子格网法;涡格法;片条理论;模态局部化
T型尾翼是指平尾位于垂尾稍部,平尾和垂尾组成一个“T字”结构形式的尾翼。T型尾翼结构具有诸多优点,一方面,T型尾翼布局可使平尾避开机翼尾流或尾吊发动机喷流的影响,增大平尾力臂、提高操纵效率;另一方面,T型尾翼构型可以实现后机身大开口,便于大型装备的货物装运。因此,许多大型军用运输机和尾吊发动机布局的民用客机都选择T型尾翼布局。现有研究结果表明,T型尾翼的颤振速度一般要比常规布局尾翼的颤振速度低,特别需要注意的是,如果不考虑T型尾翼结构的特殊性,按照常规布局尾翼颤振计算方法进行分析,会得到偏高的T型尾翼颤振速度[1]。因此对T型尾翼颤振速度的准确计算是T型尾翼布局飞机设计中的一项关键工作,更是保证大型T型尾翼布局运输机颤振安全的重要工作。
本文从T型尾翼的工程颤振分析方法出发,讨论了T尾颤振的特点,影响T型尾翼颤振特性的关键参数,介绍了T型尾翼颤振计算的四种分析方法:基于修正片条理论、修正的偶极子格网法(DLM)、修正涡格法(VLM)和气动力导数因子法的T型尾翼颤振计算方法。特别提出在T型尾翼颤振计算中,对平尾的气动力进行修正时,计算平尾定常气动力所取速度值应该与颤振速度相匹配,以提高T型尾翼颤振速度计算的精度。
1 T型尾翼颤振的特点
T型尾翼的结构特点,使得其颤振特性与常规布局尾翼有很大不同,除了在颤振分析计算时需要考虑后机身柔度的影响外,T型尾翼的颤振特性还具有两方面的特点。从气动力方面讲,常规布局尾翼颤振计算中不需要考虑的平尾定常气动力(静升力),在T尾颤振中却不可忽略,因为当垂尾发生弯曲振动而带动其稍部的平尾滚转运动时,作用在平尾上的定常气动力在水平和垂直方向上的分量也成为时变的气动力,从而使平尾静升力产生所谓的非定常气动力效应(因而平尾的攻角也成为颤振计算中必须考虑的参数),显然,进行T尾颤振计算时,如果仍然按常规非交互升力面的处理方法计算T尾的非定常气动力,则还应该采用某种方法对T尾的非定常气动力进行修正以计及这种非定常气动力效应的影响;从结构方面讲,通常T型尾翼颤振研究基于T型尾翼是理想对称结构模型基础之上,进行相应的数值计算和试验研究。然而在实际的T型尾翼结构中,由于制造和装配上存在的误差,可能导致T型尾翼对称结构的失调,这种失调会引起T型尾翼结构的振动模态局部化,进而显著改变T型尾翼结构的振动模态和颤振特性。因此,T尾颤振的工程分析方法以及T尾结构参数对T尾颤振的影响等问题都需要进行深入的研究。
2 T型尾翼颤振的影响参数
从颤振机理上讲,常规布局尾翼的垂尾颤振一般为垂尾弯曲与扭转模态的耦合,而T型尾翼构型的颤振模态通常也表现为垂尾的弯曲与扭转模态的耦合。但T尾颤振表现为:
第一,位于垂尾顶部的平尾,增加了垂尾弯曲、扭转自由度的质量和惯量,使垂尾振动的固有频率显著减小;
第二,一方面,平尾上的定常气动力引起平尾气动弹性静变形,从而影响平尾上的定常气动力分布,另一方面,垂尾的弯曲振动,使平尾发生滚转运动,引起平尾定常气动力水平和垂直方向的交变效应,从而在颤振计算必须予以考虑。如果不考虑平尾运动扰动的气动力影响,会使得计算的颤振速度偏高,安全裕度较低。
第三,平尾的端板效应,改变了垂尾的压力中心和升力线斜率,平尾几何上反角和由于平尾后掠角引起的上反角效应也将影响平尾上的非定常气动力,这些气动力都会对T型尾翼颤振特性产生影响。
第四,垂尾的扭转会引起平尾偏航,而平尾偏航会产生一个滚转力矩,滚转力矩又导致垂尾弯曲,从而引起垂尾的弯扭耦合效应。这种垂尾弯扭耦合效应随平尾尺寸的变化而改变,对带后掠角的平尾结构这种特性将更为显著。
由此可见,T型尾翼颤振特性与许多参数相关。同时,已有的研究表明,影响 T型尾翼颤振的主要参数为:
① 垂尾扭转刚度。垂尾扭转刚度与颤振临界动压存在线性变化关系,颤振临界动压随着垂尾扭转刚度的增大而增加。垂尾扭转刚度与平尾质量相关,在一定程度上确定了平尾的质量。T型尾翼垂尾翼根的垂尾扭转刚度是低平尾尾翼的1.5倍,其翼稍的刚度是低平尾尾翼的40倍[1]。
② 上反角。定义上反角符号为γ,向下为负。负的上反角越大,T型尾翼颤振速度越大[2,3]。上反角不仅影响垂尾弯扭的耦合气动力,而且上反角还直接影响垂尾刚度的设计。将平尾设计成负的上反角可以增大颤振动压,从而提高颤振速度。例如,为了减小颤振速度,5度平尾负上反角可以减小大约31%的垂尾刚度[1],也就是在颤振速度不变前提下,可以减轻垂尾的结构重量,这在结构设计中值得考虑。
③ 平尾攻角和静升力。攻角越大,平尾静升力越大,但颤振速度越小[2,3]。随着攻角或动压的增大,平尾载荷增大的更快,即平尾静升力更大,这将引起更大的静变形,导致更大的攻角和正上反角,降低T型尾翼的颤振速度。
这些关键参数对T型尾翼颤振的影响是综合相关的。T型尾翼的几何构型决定了T型尾翼结构具有较高的气动和操纵效率,因而相对地可以减小平尾尺寸和质量,但是同时垂尾的刚度和质量相对增加。但总体讲,T型尾翼的颤振特性受平尾上反角和垂尾刚度的影响较大,负的上反角和较大的垂尾刚度可以提高T型尾翼的颤振速度。
3 T型尾翼的颤振计算
模态坐标系中,T型尾翼颤振系统的广义运动方程一般可以表示为:
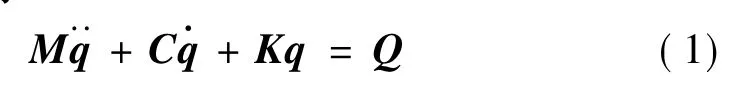
式中,q为广义坐标列阵;M为广义质量对角矩阵;C为广义阻尼对角矩阵;K为广义刚度对角矩阵;Q为广义非定常气动力矩阵。与常规布局尾翼相同的是,T型尾翼颤振计算中的质量阵M和刚度阵K是常量,容易确定,不同的是由于T型尾翼特殊的结构和气动布局,需要对其广义非定常气动力矩阵Q进行修正。由于T型尾翼气动力受平尾静升力、上反角和攻角等参数的影响,文献[4,5,6]指出T型尾翼颤振的关键影响参数是平尾攻角和上反角,是因为这两个参数直接影响平尾的静升力。非定常气动力由两部分组成,一部分是用常规非相交气动面非定常气动力计算方法如偶极子格网法(DLM)计算的不考虑平尾静升力和T型尾翼面内运动影响的广义气动力QDLM,另一部分是考虑平尾静升力和上反效应的附加广义非定常气动力矩阵ΔQ。
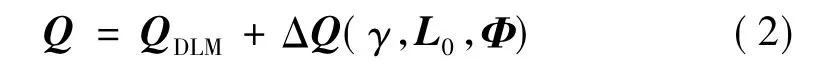
式中,QDLM为DLM计算的广义非定常气动力矩阵;ΔQ为考虑平尾静升力和上反角计算的附加广义非定常气动力矩阵,是上反角γ、平尾静升力L0和平尾模态Φ的函数。如果采用工程上常用的频域颤振计算方法,则QDLM可采用商业软件MSC.nastran计算,而对附加广义非定常气动力ΔQ的计算则需要自行编程计算。下面介绍四种常用的T型尾翼颤振计算方法。
3.1 基于修正片条理论的T型尾翼颤振计算
在平尾静升力和上反角引起的附加广义非定常气动力计算中,平尾上反角的影响通过结构模型体现,而平尾静升力引起的结构变形所产生的附加广义非定常气动力用修正片条理论计算[6]。
考虑T型尾翼特殊的气动效应后,附加的非定常广义气动力矩阵为:
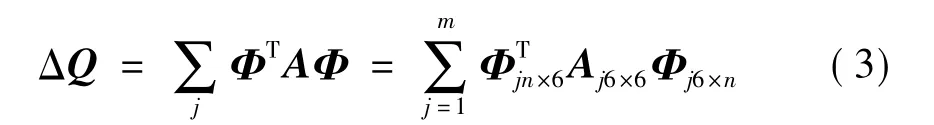
式中,m为平尾片条总数,Φj为第j个片条对应的n阶模态列阵,而Aj为第j个片条对应的气动力影响系数矩阵。
3.2 基于MSC.NASTRAN偶格法公式的T型尾翼颤振计算
文献[7]结合工程中常用的MSC.nastran软件,对T型尾翼用偶极子格网法计算的气动力进行修正。DLM是基于线性势流理论,不考虑参考速度下每个升力面盒上的扰动,而这种扰动对平尾较为明显,影响了垂尾弯扭模态与平尾弯扭模态间的耦合。由于这些扰动本质上是由平尾面内位移和升力扰动(上反角)引起水平安定面的静变形所产生,因此,可以对不同振型的变化,加入其定常升力的影响来进行气动力修正。
MSC.nastran气弹手册[8]中给出的广义非定常气动的计算公式为:
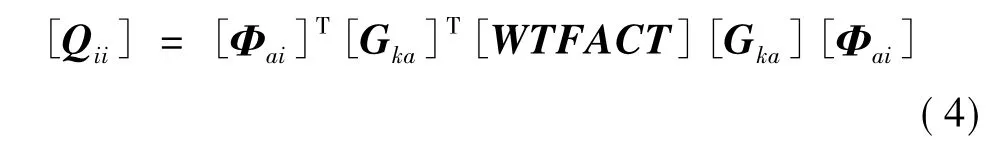
在式(4)中,Qii为广义非定常气动力矩阵,Φai为正则模态矢量矩阵,Gka为样条插值矩阵,WTFACT为修正因子矩阵。
记未修正的广义气动力矩阵为[QHH0],修正后的广义气动力矩阵表示为:

颤振分析中的广义矩阵[QHH]为每个减缩频率对应的气动力矩阵。因此[QHHL]为第三维为减缩频率序列的一个三维矩阵,修正中实际计算每个减缩频率下的[ΔQHH]矩阵。
前述两种以DLM为基础的气动修正方法应用比较广泛,其不同点在于T型尾翼附加广义非定常气动力的计算方法不同,前者是使用修正片条理论进行修正,而后者是考虑振型扰动下的偶格法公式修正。
3.3 基于修正涡格法的T型尾翼颤振计算
文献[9]在风洞试验时发现,反对称颤振(由垂尾的弯曲和扭转模态耦合而发生)的临界速度很大程度上取决于平尾的变形和攻角。这种特殊的反对称颤振与T型尾翼的其它类型模态耦合颤振相比,特点在于平尾在X轴方向有大振幅振动(X轴为机身轴,沿气流方向)。因此,V.D.Chuban通过在振动位移分量的X方向增加面内振动的诱导阻力来解释反对称模态耦合颤振的问题本质[9]。主要考虑了两点:(1)给定有限的攻角、侧滑角和控制面偏角,其引起的有限正则矢量振动不穿过边界层;(2)引入关于线性气动力的小量弹性振动,允许存在诱导阻力,在线性化的过程中诱导阻力与气动力相加。
基于修正涡格法的T型尾翼颤振计算方法,考虑了平尾面内运动的显著影响和面内振动的诱导阻力对颤振临界速度的影响。数值算例结果表明,攻角和平尾变形对颤振临界参数有明显影响。但是,这种方法的计算精度不高,存在22%到39%的误差,这在实际工程中是不允许的,而出现如此大误差的原因是修正涡格法采用了准定常气动力理论。
3.4 基于广义气动力导数因子法的T型尾翼颤振计算
T型尾翼颤振计算中,用片条理论计算附加气动力存在两个缺点:第一,缺少通用性;第二,程序不能自动运行,需要人工干预,降低了计算效率。为此,Emil Suciu提出了气动力导数因子法[10],用数值方法来控制气动力升力面间基于DLM的力和力矩。广义气动力导数因子法适合于控制所有气动力和力矩的交互影响。
气动力导数因子法的修正矩阵可以表示为修正气动力和修正气动力矩:

每个Fij为一个4 ×4 的片条修正矩阵,a1、a2、a3和a4分别为4个运动分量的修正因子系数。而这些修正因子是通过计算给定减缩频率k下每个单元上的气动升力L和广义气动力Q得到。例如L=a1×Lh+a2×Lα+a4×Lβ+a4×Lδ。因为各运动模态是各自独立的,所以用修正因子可以修正片条升力,从而实现T型尾翼颤振程序的自动化运行,这就是问题的关键。但是,修正因子又必须通过试验分析确定,结合灵敏度分析,了解各个因子的影响特性。如果给定飞行条件,用非定常气动力理论DLM修正各个运动模态的因子,就可以得到更近似解。
以上四种T型尾翼颤振计算方法各有其特点,其关键在于考虑平尾的广义非定常气动力修正计算。工程中常用片条理论计算平尾静升力引起的附加广义非定常气动力,结合MSC.nastran软件进行T型尾翼颤振计算。基于MSC.nastran偶极子格网法气动力修正的T型尾翼颤振计算有益于工程颤振分析,修正涡格法的T型尾翼颤振计算提供了新的方法,广义气动力导数因子法的T型尾翼颤振计算对提高求解精度和速度有参考意义。从平尾上的定常气动力引起附加非定常气动力效应的原理可知,T型尾翼颤振耦合模态中,气动力修正对T尾反对称模态耦合的颤振特性影响比较显著。
4 T型尾翼颤振计算中应注意的问题
研究T型尾翼颤振计算方法的最终目的,是为了提高计算精度,得到T型尾翼真实的颤振特性。下面我们给出一些T型尾翼颤振分析中应注意的问题,以加深对T型尾翼颤振分析和T型尾翼颤振特性的理解。
第一,T型尾翼颤振计算精度。T型尾翼的工程颤振计算通常用片条理论计算平尾静升力引起的广义附加气动力,计算平尾静升力的动压条件必须与飞机的颤振状态相匹配以提高T型尾翼颤振的计算精度[11]。
第二,模态局部化对T型尾翼颤振特性的影响。模态局部化是弱耦合对称结构中一种不可预期的动力学现象。作为典型的镜像对称结构,飞机T型尾翼结构的地面振动试验中通常会发生强烈的模态局部化现象,使得T型尾翼结构模态局部化研究成为T型尾翼结构设计中一个重要的力学问题。本文作者在文献[11-13]中基于失调T型尾翼结构的气动弹性特性,提出了T型尾翼颤振失调设计的概念,分析了平尾翼尖的质量失调设计和平尾根部的刚度失调设计,及其失调产生的模态局部化对T型尾翼颤振特性的影响。由于失调后T型尾翼结构的模态局部化引起固有振型的剧烈变化,对T型尾翼广义非定常气动力会产生较大影响,从而会影响T型尾翼颤振特性。与对称结构参数失调相关的模态局部化问题在T型尾翼颤振分析中将成为新的影响参数。在T型尾翼布局的飞机设计中,这个现象应该引起足够的重视。
5 结论
(1)基于修正片条理论的T尾颤振计算方法,常与MSC.nastran软件结合,便于工程计算;基于 MSC.nastran的偶极子格网法气动力修正的T型尾翼颤振计算有益于工程颤振分析;基于修正涡格法的T型尾翼颤振计算提供了新的方法,但是其精度有待提高;基于广义气动力导数因子法的T型尾翼颤振计算对提高求解精度和速度有参考意义。
(2)对平尾的非定常气动力进行修正后,由于气动力修正对T型尾翼临界颤振情况的反对称模态效果显著,T型尾翼颤振临界模态通常由反对称模态引起,因此要关注反对称模态;
(3)为了提高计算精度,平尾定常气动力的计算速度应该与颤振速度相匹配;
(4)与失调相关的模态局部化问题在T型尾翼颤振中将成为新的影响参数。
[1]Byrnes A L,Hensleighj W E,Tolve L A.Effect of horizontal stabilizer vertical location on the design of large transport aircraft[J].Journal of Aircraft,1966,3(2):97 - 104.
[2] Robert T.Taylor,Edward,J.Ray.Factors affecting the stability of T - Tail transports[J].Journal of Aircraft,1966,3(4):359-364.
[3] Shigeo Kobayashi.The State Of The Art In Aeroelsticity Of Aerospace Vehicles In Japan.University Of Tokyo Bunkyo-Ku,Tokyo,Japan 1973,3.
[4]Jennings W P,Berry M A.The flutter analysis of T-Tails[J].AIAA Journal,1975,759:1 -4.
[5]Jennings W P,Berry M A.Effect of stabilizer dihedral and static lift on T - Tails flutter[J].Journal of Aircraft,1977,14(4):364-367.
[6]Emil Suciu.MSC/NASTRAN flutter analyses of T-Tails including horizontal stabilizer static lift effects and T-Tail transonic dip[C].The 1996 Msc/Nastran World User’S Conference.Newport Beach.CA,June,1996:1-10.
[7] Quarantal G, RiccilS, ScottilA, etal. Aeroelastic investigation and design improvements on a three surface transport airplane[C].XVIII Congresso Nazionale AIDAA.Settembre,2005.VOLTERRA(PI):19 -22.
[8]Rodden W P,Johnson E H.MSC/NASTRAN Aeroelastic Analysis User’s Guide.V68[M].The Macneal Schwendler Corporation,1994.
[9]Chuban V D.Influence of angle of attack and stabilizer deflection on T empennage flutter[J].Journal of Aircraft.2005,42(1):264-268.
[10] Emil Suciu.A general aerodynamic derivatives factoring method for the MSC.Nastran DLM capable of controlling all lifting surfaces aerodynamic forces and moments,including all interference effects[C].The MSC/Software 2003 Virtual ProductDevelopmentConference. Dearborn, Michigan,USA.2003,39.
[11]杨 飞.飞机T尾结构模态局部化及颤振特性研究.[D].西安:西北工业大学,2009,3.
[12]杨智春,杨 飞.模态局部化对T尾颤振特性的影响[C].第十一届全国空气弹性学术交流会论文集,2009,8:364-370.
[13]杨 飞.模态局部化对T尾颤振特性的影响[J].振动与冲击,2010,29(8):1 -4.
Some key issues of aircraft T-Tail flutter calculation
YANG Fei1,YANG Zhi-chun2
(1.Strength Department,Shanghai Aircraft Design And Research Institute,Shanghai 200232,China;2.School of Aeronautics,Northwestern Polytechnical University,Xi’an 710072,China)
The flutter calculation method for convensional aircraft tail wing can not be used directly to T-tail flutter analysis due to T-Tail features in structural and aerodynamic configurations,and the effects of in-plane motion and steady aerodynamic force of horizontal plane must be considered in T-tail flutter calculation.From the view point of engineering analysis for T-tail flutter,some key issues of T-tail flutter calculation were discussed here,the characteristics of T-tail flutter problem and the key parameters affecting T-tail flutter properties were described.Especially,four methods to correct aerodynamic force of T-tail in its flutter calculation were intrduced and finally some specific problems to be noticed in T-tail flutter analysis were presented.
T-Tail;flutter;aerodynamic force;doublet lattice method(DLM);vortex lattice method(VLM);strip theory;modal localization
V215.3
A
国家自然科学基金(10672135);教育部新世纪优秀人才支持计划(NCET-04-0965)资助
2009-11-30 修改稿收到日期:2010-03-15
杨 飞 男,硕士,1982年12月生

