基于响应面的大型输电塔结构有限元模型动力修正

程霄翔，费庆国，何顶顶，韩晓林

(东南大学 土木工程学院，南京 210096)

基于响应面的大型输电塔结构有限元模型动力修正

程霄翔，费庆国，何顶顶，韩晓林

(东南大学 土木工程学院，南京 210096)

针对基于灵敏度分析的有限元模型动力修正方法计算效率较低、迭代收敛慢的不足，将响应面法引入500 kV大跨越输电塔基准模型修正。选择塔脚弹性支承刚度为修正参数，依次进行单因素试验、样本值计算、响应面建立与分析、参数优化。修正后，有限元模型非常准确地复现了单塔横、纵两个方向的一阶弯曲动态特性，修正效果与基于灵敏度分析的模型修正方法接近，证明响应面法在有限元模型动力修正领域的应用价值。还探讨了塔架结构修正参数的选取问题，为相关研究提供参考。

模型修正;响应面法;大型输电塔;参数选取;动态特性

有限元模型修正是一个通过逐步修正模型参数使得有限元计算结果与测试值尽可能接近的迭代优化过程，目前针对大型工程结构的有限元模型修正通常基于灵敏度分析。对单元数目众多的结构模型修正，如采用基于灵敏度分析的方法，每次迭代都要调用有限元程序求解高维非线性方程，计算量大。

针对通常模型修正方法的不足，费庆国等将响应面法引入模型修正领域，通过修正GARTEUR飞机模型验证了该方法的有效性［1］。响应面模型修正法的主要步骤为:① 利用试验设计方法在参数的设计空间内确定样本点，在样本点上进行有限元分析计算获得样本数据;② 基于方差分析在整个设计空间筛选对于特征量有显著影响的设计参数;③ 以显式响应面模型逼近特征量与设计参数间的复杂隐式函数关系;④ 在等效模型的基础上进行设计参数的优化。整个修正过程避免了有限元计算，提高了效率。任伟新等基于响应面法修正桥梁结构模型，亦获良好效果［2］。

大型输电塔为高耸柔性结构，塔体构成复杂、不确定性参数比较多。理想设计状态的塔模型较实际工程往往存在偏差，不能满足结构健康监测及安全评估需要。为了深入开展输电塔基准模型的修正研究，必须选择合适的修正方法。并加以验证。本文将响应面法引入大型输电塔有限元横型修正，以某高度131 m的新建500 kV大跨越输电塔为工程背景，详细介绍了该塔面向结构健康监测的基准有限元模型的修正过程。

1 初始塔模型的模态分析

研究以某500 kV大跨越输电塔为工程背景。该塔为SKT直线跨越塔，整塔设计高度131 m，塔头宽度6 m，跟开26 m，干字形塔。该塔系钢管与角钢组合空间结构，主体由四根主弦杆以及弦杆之间的横杆、斜撑杆、腹杆构成，上下横担均由钢管和角钢组合构成。

依照相关资料，研究人员基于某有限元软件平台建立了初始模型，模型采用混合单元建立以保证整体刚度准确性(图1)。塔身主体主要由钢管通过法兰或插板以对心连接方式构成(图2)，节点的刚度大，故用梁单元模拟杆件;一些次要部位由角钢通过插板连接和焊接以偏心方式构成(图3)，有限元模拟采用杆单元。

文献［3］详细介绍该塔的基准动态特性实测，测试基于环境激励下的加速度响应信息，使用输出可测条件的模态参数识别技术获取了单塔的低阶模态，测试结果为结构有限元模型修正提供依据。表1对比了初始塔模型实测、计算模态。由表1，尽管计算模态振型与实测值一致，但模态频率误差大，且具有相对误差依阶次顺序递减的特点，一、二阶相对误差(14% ～16%)远大于三～五阶(1%～6%)。模型修正以减小横、纵向一阶弯曲模态频率误差为主要目标。

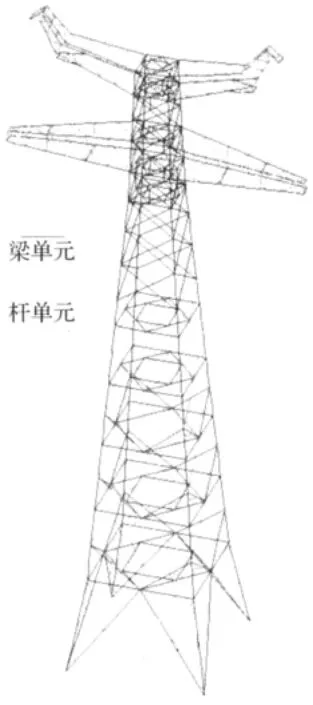
图1 初始有限元模型Fig.1 3D view of initial finite element model

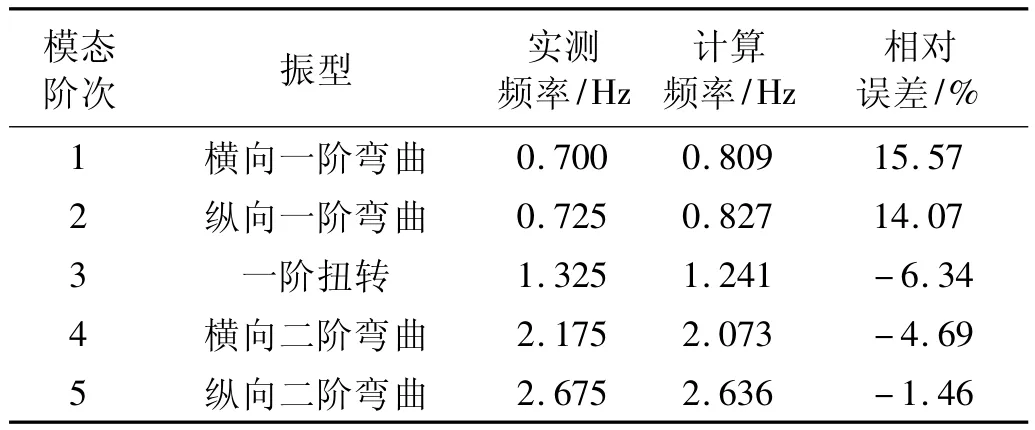
表1 初始模型模态频率计算值与测试值Tab.1 Modal frequency differences between analyzing and testing results before updating

图4 有限元模型一至三阶模态振型Fig.4 View of first three modes of vibration obtained by FE model

2 修正参数的选取

修正参数必须与理想状态有较大偏差并对模型动态特征量有显著影响，应在整体结构范围内筛选。对于输电塔模型，可选择的修正部位包括塔身杆件、连接节点、边界等，依据实际状况逐一分析:

(1)塔模型单元的弹性模量、密度、截面积等较设计值可能有一定偏差，因此研究人员首先将本塔塔身的关键杆件设计参数作为修正参数，开展了基于灵敏度分析的动力模型修正，参见文献［4］。值得注意的是，研究对象是新建工程，构件无累积损伤、老化和锈蚀，修正参数的变化范围不应偏离设计值过大。

(2)节点方面，文献［5］认为高耸塔架结构有限元模型的不确定性主要来自节点。实际大量节点属半刚性连接，有限元模型杆件的连接刚度较实际情况存在差异。针对这一问题，文献［6］基于不同类型单元建立了5个500KV猫头塔有限元模型以模拟节点刚度的差异，对比计算结果发现节点刚度大小仅对塔模型的一些高阶模态产生影响，对于低阶动态特性影响不大。

(3)研究对象建立在4个钢筋混凝土承台之上，各承台由9根混凝土桩支承，基础和周围土层间存在相互作用。由文献［7］，在软土或中软场地，桩－土－结构动力相互作用对输电塔的影响不能忽略。文献［8］在修正某海洋平台模型的过程中将地基模拟为三维弹性支承并使用了基于灵敏度分析的优化方法修正支承刚度，结果表明三维弹性支承的刚度大小对于海洋平台结构有限元模型的低阶基频(主要为一～三阶)影响大，对于模态振型的影响小。

文献［4］选择塔身主弦杆和斜撑杆等关键杆件为修正对象，进行了基于灵敏度分析的模型修正，研究发现关键杆件的截面和弹性模量参数对模型动态特性不显著，修正后模型的部分低阶模态频率和测试结果之间仍然存在不小的误差。表2给出弹性模量修正结果，选择0.001为每次迭代修正的弹性模量变化率，在迭代98次时，弹性模量的总变化率超过10%，因偏离设计值过大，终止迭代。修正后模型的一、二两阶模态频率误差仍然比较大。因杆件参数修正没有获得理想的效果，必须考其它修正对象。

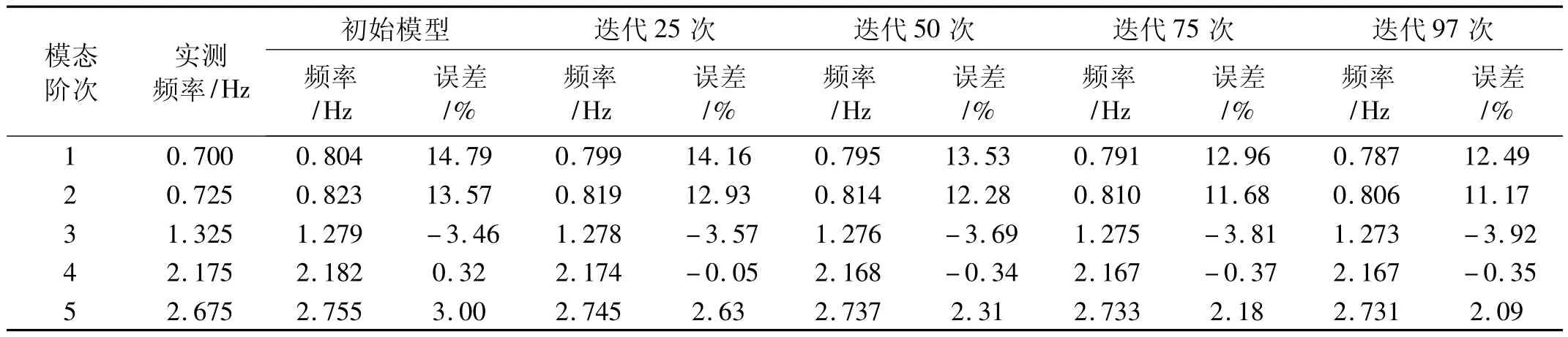
表2 部分单元弹性模量变化率0.001修正结果Tab.2 Influence of key elements’elastic modulus change(0.001 constant changing rate)on FE model frequcency

经上述分析，本文最终选择三向边界支承刚度这些具有明显不确定性并且对于特征值影响显著的参数加以修正。采用与文献［8］类似的方法模拟边界条件(用弹簧单元模拟三向平动支承，约束三向转动自由度)，将三个方向的弹簧弹性刚度作为修正参数。

3 响应面法的理论基础

响应面方法是试验设计与数理统计相结合的方法，基于响应面的有限元模型修正理论主要包括试验设计、参数筛选、响应面拟合以及参数优化。

3.1 试验样本集的选取

为了保证响应面模型的精度，降低有限元计算量，样本集的选取基于试验设计方法。试验设计方法有析因实验设计、中心复合设计(CCD)、Box－Behnken设计以及D－最优设计等。

中心复合设计是其中较为常用的试验设计方法，它包含三类试验:① 根据每个因素的±1两个水平值(分别代表该因素的最大和最小水平)，利用正交表构造试验方案，进行n次试验;② 在中心点(0，0，…，0)作n次重复试验;③ 在各因素坐标轴上臂长±a点处进行2m次(m个因素)试验。因此样本集包含的样本点总数:

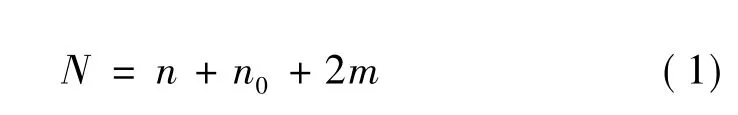
3.2 参数筛选

方差分析的基本思想是将样本数据的总偏差平方和分解为各因素以及误差的偏差平方和，求出F值，应用F值检验法进行假设检验，找出显著性参数。假设对有限元模型的设计参数(因素)A进行F检验，统计量为:

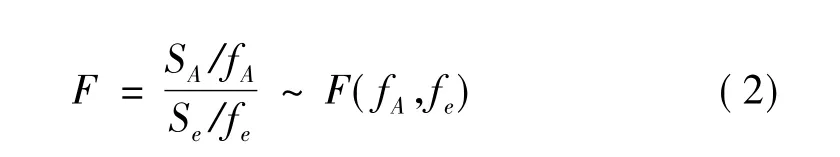
式中SA为因素引起的偏差平方和，Se为误差的偏差平方和，fA、fe分别为因素A和偏差的自由度。对于给定的显著水平 α，F 检验的法则为:若 FA≥F1－α(fA，fe)，则认为设计参数A影响显著，否则认为不显著。依据F显著性检验的结果，进行参数筛选，修改响应函数的形式。

3.3 响应面拟合

有限元模型修正中，通常将二次多项式作为响应函数，得到样本集之后，一般利用最小二乘回归分析来确定。

令系统的特征量y为因变量，设计参数为xi，i=1，2，…，k。若采用次多项式响应函数，则回归方程形式:

在试验设计确定的样本点，通过有限元分析获得的样本数据y1，y2，…，yn;将设计参数与特征量的样本数据代入式(3)，采用最小二乘法可估计多项式系数β0，β1，βij，βii。

通常响应面的精度依据式(4)判断:

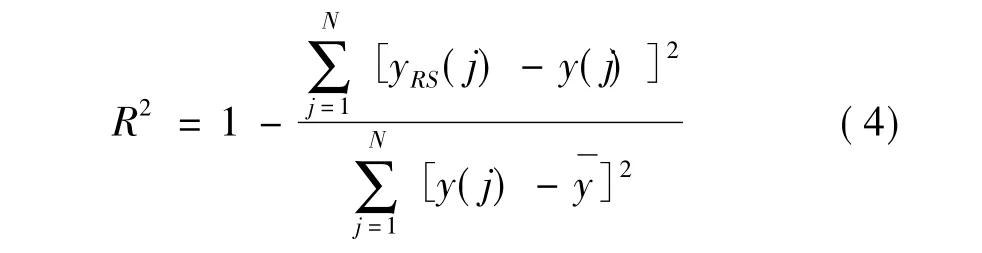
其中，yRS(j)代表响应面模型的计算值，y代表真值(有限元分析的计算结果)，y代表真值得平均值。R2值越大，则得到的回归模型就越接近实际情况。经检验，若响应面模型精度符合要求，则进行设计参数修正;不符合，应增加样本点，重新试验设计。

3.4 参数优化

模型修正可归结为以下的优化问题:

其中，p代表设计参数，{fE}，{fA}代表特征量，分别是分析与试验的结果，VLB，VUB是设计空间的边界，R代表特征量的残差。

4 基于响应面法的输电塔模型动力修正

针对塔脚三向支承刚度分别开展单因素数值试验，依据结果确定待修正参数的合理取值范围。后借助试验设计软件Design-Expert(Version 6.0.10)完成基于响应面法的单塔模型修正。对比基于灵敏度分析的模型修正方法，验证模型修正效果。

4.1 单因素有限元试验

表2给出了约束模型塔脚除竖向以外的5个方向自由度，采用不同大小的基础竖向支承刚度(大小范围在108N/m～109N/m)的有限元模型计算模态频率。将表3给出的结果作为基准数据，通过三次多项式差值获得了模型计算模态频率随基础竖向支承刚度的变化曲线(图5)。

同理，单独改变基础横、纵向支承刚度的大小，约束塔脚其余各方向的自由度(基础刚度视作无穷大)，可以考察由此产生有限元模型计算模态的改变，结果由表4和图6、图7给出。

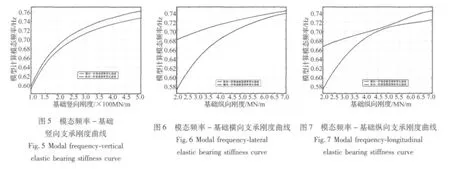
表3 基础竖向支承刚度在100 MN/m ～500 MN/m范围内的有限元模型计算模态频率Tab.3 Influence of vertical elastic bearing stiffness ranging from 100 MN/m～500 MN/m on analyzing modal frequency of FE model

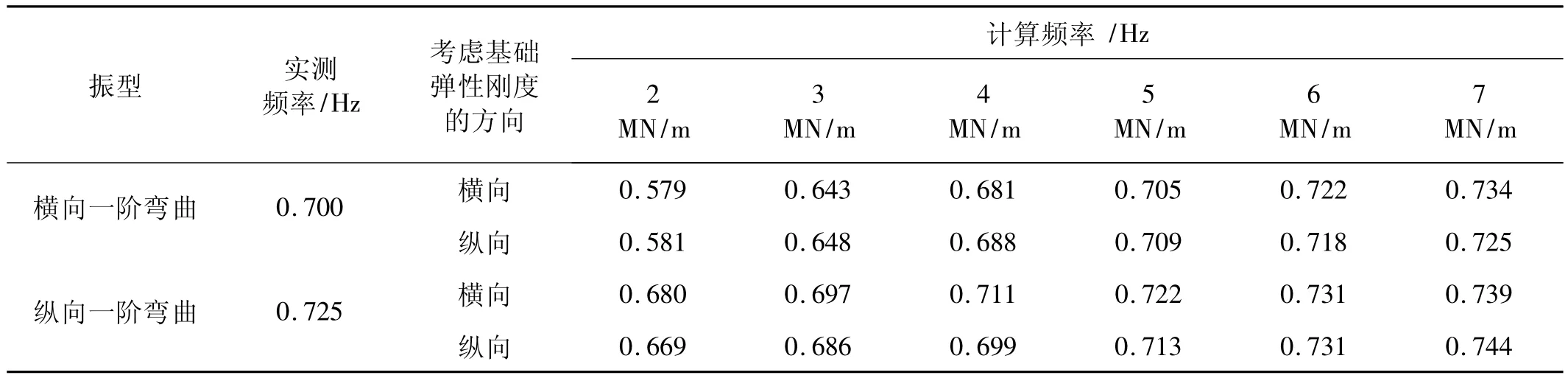
表4 单独考虑基础横、纵向支承刚度的有限元模型计算模态频率Tab.4 Influence of horizontal elastic bearing stiffness on analyzing modal frequency of FE model(lateral and longitudinal direction)

数据对比分析可知:① 模型的计算模态频率随各平动方向刚度的增加而增大，符合基本规律;② 基础竖向支承刚度的改变对于纵、横向一阶弯曲频率的影响程度相当，改变基础侧向(纵、横)刚度产生的模型横向一阶弯曲振型频率的变化远大于纵向一阶弯曲振型的变化。

4.2 基于中心复合设计的样本值计算

竖向支承弹性刚度使用式(6)估算:

式中，E、A和H分别为桩的弹性模量、有效截面面积、有效长度。计算得本工程基础竖向刚度为3.72×109N/m。对于水平方向(横、纵向)支承的弹性刚度，缺乏普遍认可的估算方法，是具有明显不确定性的参数。各向弹性支承刚度参数范围应相对慎重选取，参照单因素有限元试验结果确定各待修正参数的取值范围如表5。

表5 中心复合设计主要参数范围Tab.5 Updating parameter bounds

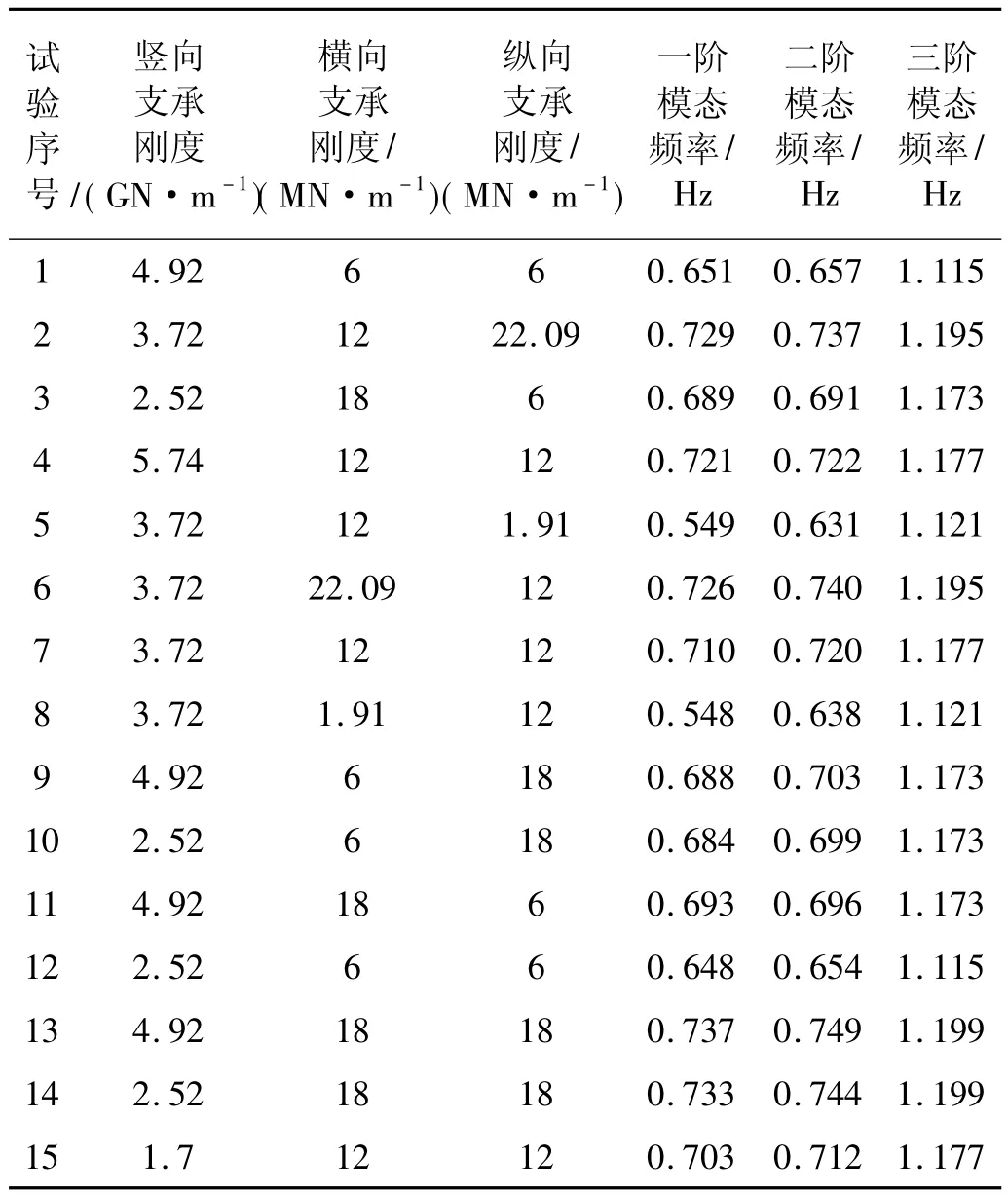
表6 基于中心复合设计的有限元试验结果Tab.6 FE experiment results based on central composite design

以表5中各个参数为因素，利用中央复合设计原理，在参数的设计空间内确定了15个样本点(α值取1.681 79)。在样本点上进行有限元分析计算，获得相应样本值(塔模型一至三阶计算模态频率)。表6给出有限元试验结果。

4.3 响应面模型的建立

使用专业软件完成试验数据回归拟合。先检验二次回归模型中各样本参数对于特征量的显著性:由表7给出的F检验(显著性阀值5%)结果，一些因素的Prob＞F值大，显著性弱。因一、二阶频率模型中交叉项不显著，响应函数应采用完全二次多项式;对于一、三阶频率模型，样本参数A不显著，去除参数A，保留B、C。

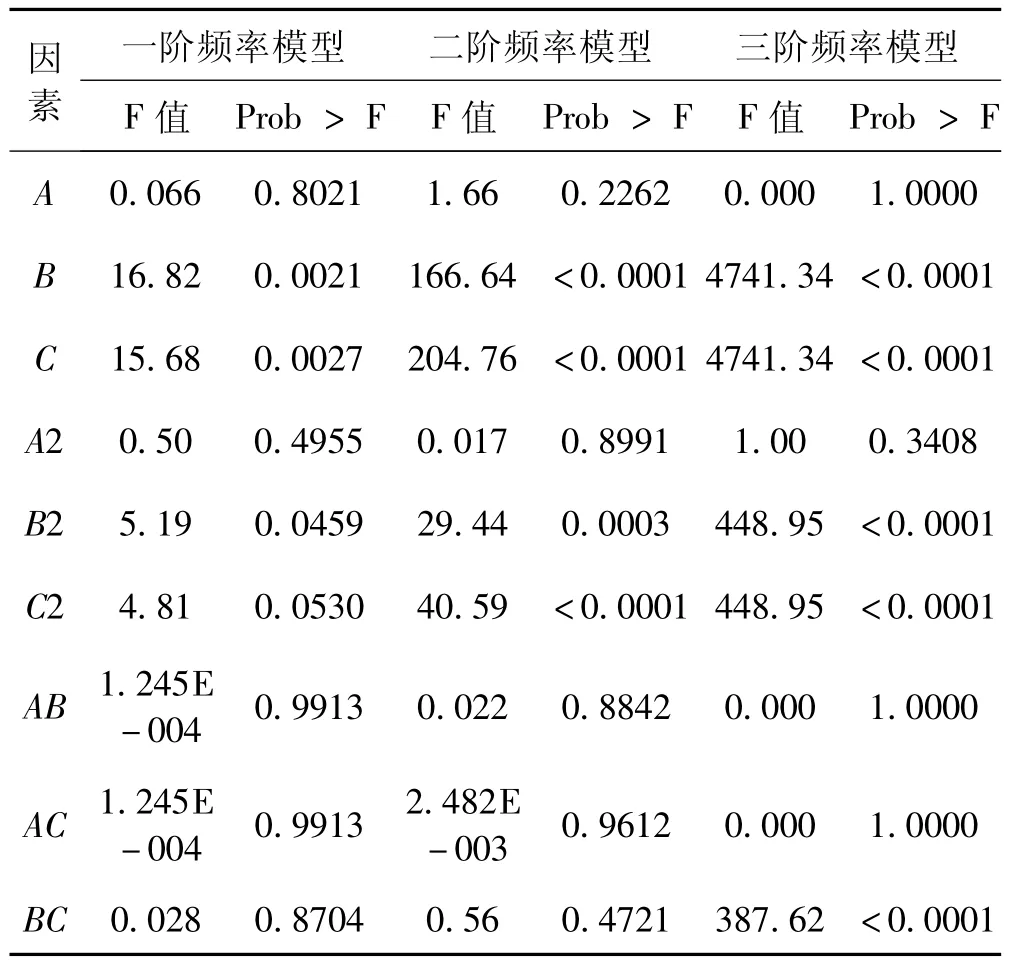
表7 二次模型的系数显著性检验(阀值5%)Tab.7 Results of significance test on quadratic model coefficients(significance threshold 5%)

表8给出调整后回归模型的显著性检验结果，各模型显著性好、失拟项不显著、拟合程度佳，可作为分析各向支承刚度与低阶模态频率之间的关系的依据。以一阶频率模型为例，模型的 F=14.99＞F0.05，F ＜0.000 1，表明回归模型极其显著，而失拟项不显著;R2检验结果为0.799 9，说明该模型拟合程度较好，试验误差小;充分精度(信噪比)远大于4，说明具有足够的信号，模型拟合在整个设计空间范围有效。由调整后回归模型的系数显著性检验(表9)可知，各阶频率模型的一次项B、C都极其显著，二次项B2、C2极显著，对于三阶频率模型交互作用不可忽视。各个因素对于模态频率的影响不是简单的线性关系。

采用最小二乘法估计多项式的系数，获得各响应面模型。图8～图10给出各模型的响应面图谱。

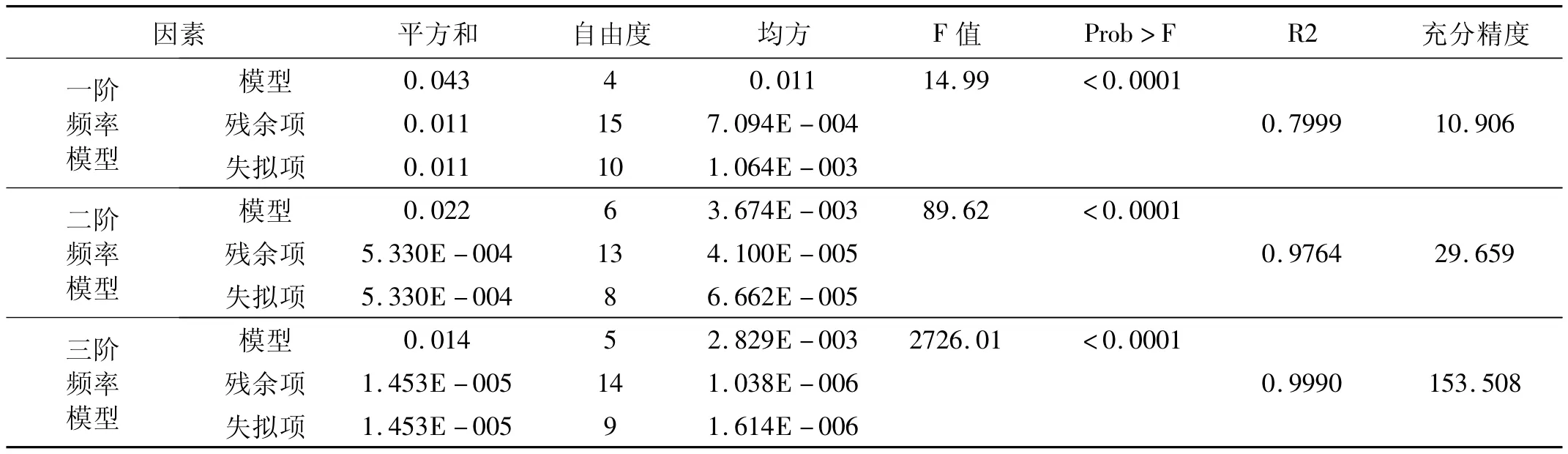
表8 调整后回归模型的显著性检验Tab.8 Significance test results of adjusted regression model

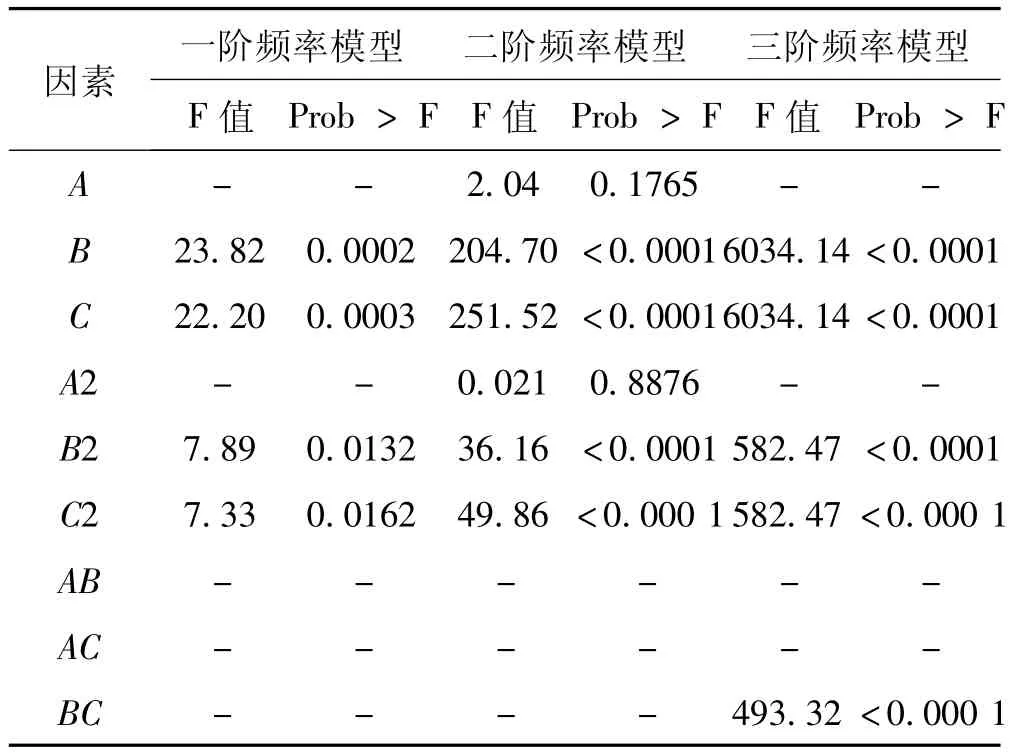
表9 调整后模型的系数显著性检验(阀值5%)Tab.9 Results of Significance test on adjusted model coefficients(significance threshold 5%)

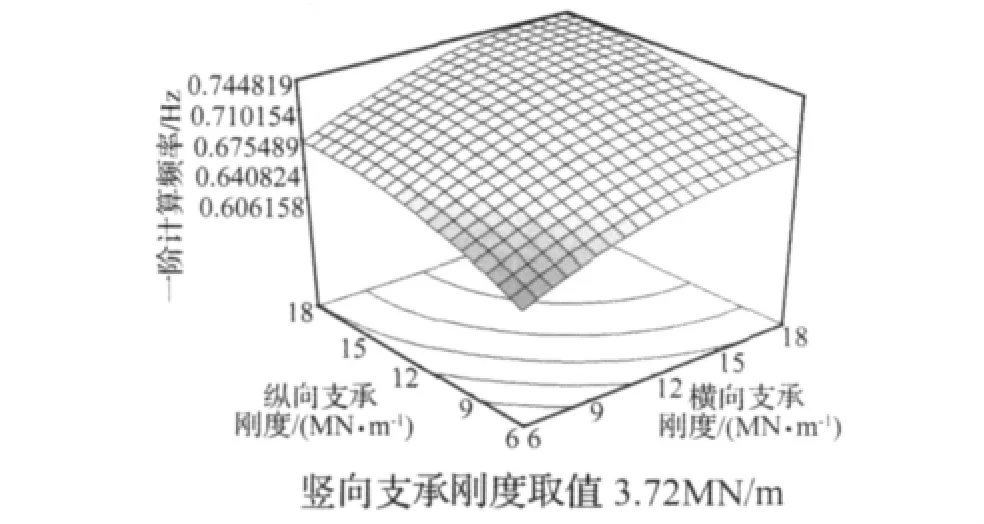
图8 基础横、纵向支承刚度对一阶模态频率响应面Fig.8 Response surface view of primary modal frequency

4.4 响应面分析

响应曲面及其等高线直观地反应了各向支承对于低阶模态频率的影响。

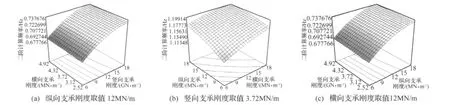
图9 基础各向支承刚度对二阶模态频率响应面Fig.9 Response surface view of secondary modal frequency

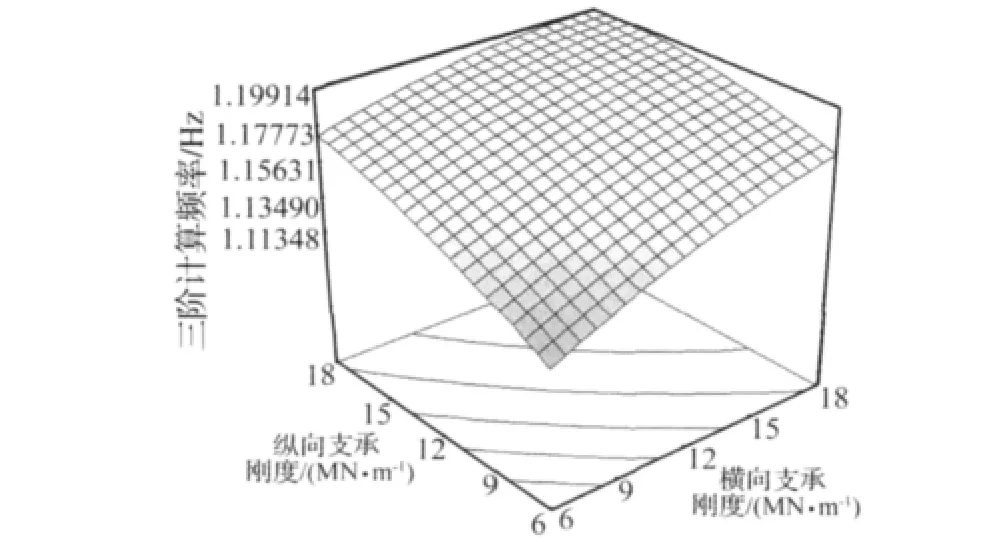
图10 基础横、纵向支承刚度对三阶模态频率响应面Fig.10 Response surface view of tertiary modal frequency

当竖向支承刚度固定在零水平，即3.72 MN/m时，纵、横向支承刚度对一阶频率的影响见图8。由图8，在设计参数的整个空间内，频率随着支承刚度增大而不断增加。曲线较陡，曲面形状变化大，说明水平方向支承刚度变化对于一阶频率的影响显著。等高线的形状反映了两种因素交互作用的显著性，一般来讲，椭圆表示交互作用显著，圆形相反。可以发现纵、横两向支承刚度对一阶频率的交互作用不显著。

观察图9，尽管二阶频率随三向支承刚度的增大而增加，但水平(横、纵两个方向)支承刚度对于二阶频率的影响显著性明显强于竖向支承刚度。图9中等高线呈圆形，纵、横两向支承刚度的交互作用不显著。图10，三阶频率模型中纵、横两向支承刚度的交互作用显著，这与表3中F检验的结果一致。

比较图8、图9(b)、图10，纵、横两向支承刚度对于一、二两阶模态频率的影响显著，对三阶频率显著性略差。综合响应曲面直观分析及模型显著性检验结果，水平向(纵、横两向)支承刚度对于模型低阶(尤其为一、二阶)模态频率的影响大，为重要待修正参数。

4.5 修正参数优化

参数优化基于响应面模型，优化获得竖向、横向和纵向的支承刚度分别为4.92 GN/m、9.98 MN/m和10.51 MN/m。对优化后模型进行模态分析，优化后模型的一 ～ 三阶计算模态频率分别为 0.7、0.709、1.167，相对误差分别为 0%、2.21%、11.92%。

修正后，有限元模型获得了较好的改善，可以非常准确地复现单塔横、纵两个方向的一阶弯曲动态特性。但修正后模型存在一阶扭转模态频率的误差增大，无法精确预示修正频段以外的结构动态特性的问题。

4.6 两种模型修正方法对比

除采用基于响应面的模型修正方法，本文又基于灵敏度分析开展该塔的有限元模型修正，并对比两种方法修正效果。两次模型修正在修正参数范围、状态变量约束、优化目标函数等方面的设置完全一致。

采用基于灵敏度分析的模型修正，首先计算各参数在某设计点处对特征量的灵敏度，再选择高灵敏度的参数开展后续迭代优化。整个修正过程一直在调用有限元程序，因初始塔模型的单元众多(总单元数超过1800)，造成运算量巨大。表10给出两种模型修正方法的结果，结果对比可知，它们的修正效果接近，基于响应面方法修正后模型在一、二阶频段精度高，三阶频段误差略大。两种方法修正的模型都不具备修正频段以外的结构动态特性预测能力。

表10 两种模型修正方法的结果比较Tab.10 Results comparison between response surface-based and sensitivity analysis-based methodologies

5 结论

(1)大型土木工程结构复杂，有限元模型单元数目众多，用响应面模型替代有限元模型，可以提高计算效率，解决迭代收敛慢的问题［2］。本文使用响应面法修正某大型输电塔的初始有限元模型，修正效果与传统基于灵敏度分析的方法接近，修正后模型的一、二阶模态频率非常准确，达到了修正目的，证明了响应面法在高耸塔架模型修正中的实际应用价值。

(2)修正过程可以使用专业数理统计软件完成，易于工程应用。在建响应面模型的过程中借助基方差分析可以保证参数的显著性良好、提高等效模型的拟合精度。其中，F检验法体现了参数在整个设计范围内对特征值影响的显著性，较某设计点处的灵敏度分析更加合理。

(3)Mottershead认为，通过分析可以筛选显著性参数，通过参数微小的改变模型的预测结果与实测值趋近一致，但是参数的显著性分析结果常常不能从结构工程以及试验的角度获得合理的解释。因此，必须首先确定模型的不确定因素，并将它们参数化，再开展模型修正［9］。针对形式复杂的大型塔架结构模型，参数筛选及修正研究有待深入开展。

［1］费庆国，张令弥，李爱群，等.基于统计分析技术的有限元模型修正研究［J］.振动与冲击，2005，24(3):23－26.

［2］任伟新，陈华斌.基于响应面的桥梁有限元模型修正［J］.土木工程学报，2008，41(12):73－78.

［3］汪 江，杜晓峰，田万军，等.500kV淮蚌线淮河大跨越输电塔振动测试与模态识别［J］.中国电力，2009，42(2):30－33.

［4］何顶顶.大跨越输电塔损伤模拟分析与模型实验研究［D］.南京:东南大学，2009.

［5］查小鹏.高耸结构风致疲劳安全预警的理论和方法［D］.武汉:武汉理工大学，2008.

［6］赵滇生，金三爱.有限元模型对输电塔架结构动力特性分析的影响［J］.特种结构，2004，21(3):8－11.

［7］徐 静，李宏男，李 钢，等.考虑桩－土－结构动力相互作用的输电塔地震反应分析［J］.工程力学，2009，26(9):24－29.

［8］刘爱霞，石 湘，李华军.一种海洋平台广义模型修正方法的研究［J］.振动与冲击，2007，26(1):112－116.

［9］ Mottershead J E，Mares C，Friswell M I，et al.Selection and Updating of Parameters for an Aluminium Space-Frame Model［J］.Mechanical Systems and Signal Processing，2000，14(6):923－944.

Dynamic updating of a large transmission tower's finite element model based on response surface methodology

CHENG Xiao-xiang，FEI Qing-guo，HE Ding-ding，HAN Xiao-lin

(College of Civil Engineering，Southeast University，Nanjing 210096，China)

To conquer deficiencies of poor computational efficiency and slow convergence of traditional sensitivity analysis-based finite element(FE)model updating methodology used widely，response surface methodology was introduced into a 500kV large transmission tower's dynamic FE model updating.Based on authors'former contributions，elastic stiffnesses of the tower's three directional foot bearings were selected as parameters to be updated.Key steps in updating process including one factor test，sample on FE platform，building and analyzing response surface and parameter optimization were presented in succession，then response surface-based dynamic FE model updating was completed.The updated tower model accurately recurred the structure's primary and secondary natural frequencies，and its effect was close to that of the sensitivity analysis-based methodology，its application value was proved.The problem of parameter selection for model updating of pylon structures was also explored.

model updating;response surface methodology;large transmission tower;parameter selecting;dynamic characteristics

TU347

A

国家自然科学基金项目(10902024);国家电网公司重大科技创新项目(SGKJ［2007］1070);东南大学自然科学基金预研课题(XJ2008310)资助

2009－12－04

程霄翔 男，硕士生，1985年生

韩晓林 男，教授，1958年生