模态迭代技术的试验研究

罗银淼

(浙江大学 力学系，杭州 310027)

模态迭代技术的试验研究

罗银淼

(浙江大学 力学系，杭州 310027)

矩阵迭代法是振动系统获得模态的经典的数值方法，通常应用于有限元软件或其他数值分析领域。把该方法推广到试验模态技术领域，提出试验模态迭代法，通过假设振型以确定激振力，再激发稳态响应，数次迭代可以获得结构的模态振型。与现行结构共振试验获得模态振型思想完全不同的是，该方法同时调节激振器的激振幅值与相位，经过极少的试验周期，获得振型;振型的纯度仅仅与共振频率的试验精度有关，并且试验实现的复杂性与激振器数量无关。根据本技术进行纯模态共振试验，能极大地降低激振力调整工作量。

试验模态迭代;激振器;振型;纯模态;相位

矩阵迭代法是振动系统获得模态的经典的数值方法，常见于各类教材及其通用有限元软件或数值分析领域。通过若干次迭代，一般能获得足够精度的模态振型。作为起源于数值方法的这一迭代思想，迄今为止，相应的模态迭代法未见在振动试验应用。在模态试验技术方面，获得模态振型的试验方法最直接的就是多点激振共振试验，以获得物理分离的模态振型;特别是大型飞机结构及其火箭结构［1－3］，相应多点激振共振试验的地面振动试验(GVT)是获得振型的最普遍使用的试验方法［4－8］。

多点激振共振试验技术的重点在于选取合适的激振力个数和分布，来满足一定的模态纯度。以法国国家航空研究局(ONERA)［9］早期提出并沿用的戴克法为例，在实际试验时对某一给定的激振器激振力向量，调节其中的一个力而其它力的幅值保持不变，以满足一定的判断条件，然后再调节另一个不同的力而其它力的幅值保持不变，试验并继续以达到判断条件作为一次循环，直至得到一个满足要求的激振力向量，即为最佳激振力向量。可见该试验技术是相当繁杂并不够完善的;激振力的幅值与相位调整工作量和精度与激振器数量与调整判据有很大关系。对于大型复杂结构，需要很多激振器时，计算与试验工作量将急剧增加。为此，对于复杂结构，有报道采用假设模态法对运动柔性梁的动力特性进行研究［10］。

本文沿用经典矩阵迭代法的思想，用于纯模态试验的激振力调制，建立了基于激振力迭代的试验模态迭代技术，简化共振试验获得纯模态的力与相位调整的流程。

1 试验模态迭代法原理及其数值仿真

考虑多自由度动力系统，激振力作用下的方程:

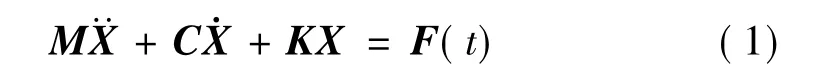
假设在一个初始状态Φ0下，激振机构作动，其作动力以Φ0进行调制:

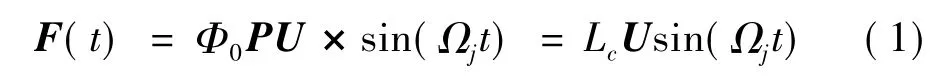
P为n×k控制力放置矩阵，U为k维作用力矢量。Ωj为系统的待试验获得的某阶纯模态振型固有频率，可以通过随机激励或正弦扫描获得。对式(1)进行模态矩阵左乘，在模态空间下X=ΦQ，系统为:

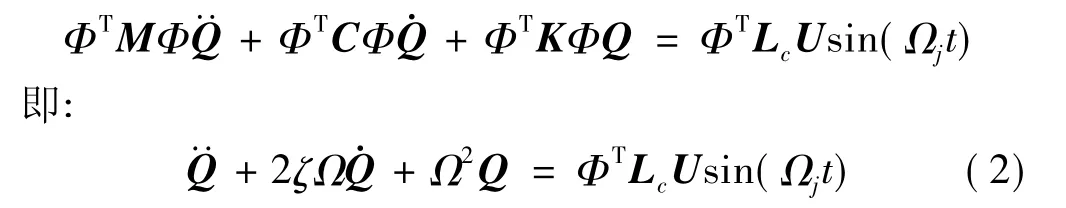
对应(2)获得的稳态响应实振幅矢量与相位为:

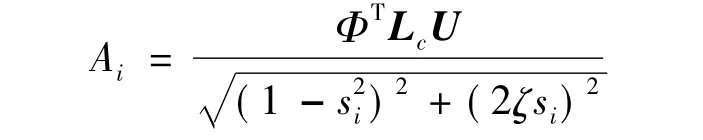
其中Ai是传感器的实测值。由于试验激振频率与j阶固有频率一致，将使得该模态自由度响应占优。以该Ai的相对比值归一化后作为新的作用力调制幅值，获得新一轮激振的稳态响应。最后m次循环后的稳态响应幅值与下式成正比:

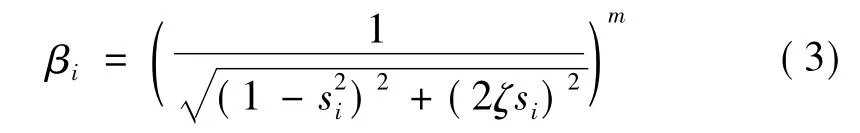
模态作用力也与(3)成比例关系，当有足够迭代次数时，在模态坐标下的非i阶自由度响应接近零，从而获得纯模态。该思想与经典的模态迭代法类似，只不过这里是通过对激振力的调制、迭代，使得获得的响应接近纯模态。

为验证该试验技术思想，首先对悬臂梁的多自由度离散系统进行了数值仿真，如图1点质量m=10 kg，

刚k=104N/m;第一个仿真例子激振器放置于点8和12;第二个仿真例子激振器放置于点6，8，10和12;一共布置6个传感器，测点位于 2，4，6，8，10和12.系统的前4阶固有频率在试验时可以通过随机激励或者正弦扫描获得，列于表1。

图1 多激振器悬臂梁共振试验系统Fig.1 Cantilever and multi-vibrator Resonant vibration system

表1 结构固有频率Tab.1structure natural frequencies

针对已经获得的某一阶固有频率，如f2=4.217 6 Hz，试验系统开始以任意初始状态启动，试验状态不依赖于任何参数。这里采用的初始状态为Φ0=0.001×［0，0，0，0，0，0，0，0，0，0，0，1］。整个仿真试验迭代仅仅耗时40s。试验结果列于表2，振型均以最后一个测点位置进行归一。识别的模态振型十分接近系统真实的模态振型，显然4个激振器的试验结果必然优于2个激振器的结果。图2为4个激振器的激振力时程输入，可以发现其相位自然为0或180°。

表2 第2阶振型识别结果(2个或4个激振器)Tab.2 Identified modal shape(2nd mode)with 2 or 4 vibrators

表3 简易飞行器结构试验模态迭代纯模态振型Tab.3 Pure mode shape by experimental iteration of a simple aerocraft model

2 试验模态迭代法的实验验证

试验模态迭代法的验证对象为一简单的飞行器结构，通过Dspace1103半实物仿真系统实现。激振器为Labworks ET－139及 LW－139－40系统 ，传感器采用pcb－356A32小型三轴ICP®加速度计。预备试验以锤击法及正弦扫描方法获得了结构固有频率基准值分别为f1=8.443 Hz，f2=24.399 Hz。分别以各阶固有频率进行试验模态迭代，获得了相应的纯模态振型，如表3所示。

3 结论

通过经典的矩阵迭代法原理，发展了试验模态迭代技术，该方法具有简洁的数学表达形式;通过数值仿真与试验验证，证明该方法简单易行，能快速获得结构的纯模态振型。与现有的结构共振试验相比，试验模态迭代技术在快速获得纯模态振型时具有明显优势。

［1］Lewis R，Wrisley D.A system for the excitation of pure natural modes of complex structures［J］.J.Aeronautical Sci，1950，17:705 －722.

［2］Hunt D.A Comparison of methods for aircraft ground vibration testing，Proceedings of the 3rd International Modal Analysis Conference［J］.Orlando，1985:131 －137.

［3］ Wright J R，Cooper J E，Desforges M J.Normal-mode force appropriation-theory and application［J］.Mechanical Systems and Signal Processing1999，13:217 －240.

［4］Boswald M，Govers Y.Taxi vibration testing-an alternative method to ground vibration testing of large aircraft［J］.Proceedings of isma International conference on noise and vibration engineering，2008，1 －8:2413 －2426.

［5］Kosmatka J B，Valdes A.Using ground vibration testing to correlate the Hunter UAV structural model［J］.Sampe journal，2005，41:5 －13.

［6］Pickrel C R.Airplane ground vibration testing-Correlation with nominal modal model［J］.Proceedings of the society of photo-optical instrumentation engineers(SPIE)，2002，4753:949－956.

［7］ Brillhart R D，Akers J C，Huber C.Multiple configuration ground vibration testing-X－34 and L－1011 carrier aircraft［J］. Proceedings of the society of photo-optical instrumentation engineers(SPIE)，2000，4062:950 －955.

［8］Pickrel C R.A practical approach to modal pretest design［J］.Mechanical systems and signal processing，1999，13:271－295.

［9］Deck A.Méthode automatique d'appropriation des forces d'excitation dans l'essai au sol d'une structure d'avion.(in French) ［C］. CongrésEuromech22 "Dynamicsof Mechanics，1970.

［10］蔡国平，洪嘉振.旋转运动柔性梁的假设模态方法研究［J］.力学学报，2005，1:48－56.

A test modal iterative method

LUO Yin-miao

(Department of Mechanics，Zhejiang University，Hangzhou 310027，China)

Matrix iteration is a kind of classic technique for obtaining modal shapes，it is used in FEM software or other numerical analyses.Here，it was extended into the field of test modal technique and a test modal iterative method was presented.Excitation force was introduced by using an assumed modal shape and a steady response was excited.Through several adjustings and iterations the modal shapes of a structure were obtained.This test modal iterative method was compeletely different from the current structureal resonance tests to get modal shapes.The amplitude and phase of actuators were adjusted simultaneously with the proposed method and less test time was needed.Modal shape's purity was related with resonance frequency test precision only.The test complexity was independent on the number of actuators.This technique could reduce excitation force adjusting work greatly.

test modal iterative method;actuator;modal shape;pure mode;phase

V216.2

A

2009－11－30 修改稿收到日期:2010－03－04

作 者 罗银淼 男，硕士，高级工程师，1965年8月生