基于频响函数辨识机械结合部动态参数的研究

郭铁能，李 玲，蔡力钢，刘志峰，赵永胜，杨 坤

(北京工业大学 机械工程与应用电子技术学院，北京 100124)

基于频响函数辨识机械结合部动态参数的研究

郭铁能，李 玲，蔡力钢，刘志峰，赵永胜，杨 坤

(北京工业大学 机械工程与应用电子技术学院，北京 100124)

进行机械结构的动力分析与动态优化设计时，为获得比较准确的结构边界条件，结合部参数辨识成为其中一项关键技术。结合工程实际，应用频响函数辨识结合部刚度与阻尼参数的方法进行参数识别，对能否获取完备频响函数进行了研究，并作出相应的求解策略。该方法避开了对频响函数直接求逆，运用最小二乘原理将矛盾方程转化为定解方程，保证了数值计算的稳定。一般情况下，结合部处绝对阻尼值要远远小于绝对刚度值，为了更准确地辨识出阻尼值，需采用对阻尼进行二次辨识。该方法具有一定的工程实用价值，而且辨识过程简单。算例证实了该方法具有很高的辨识精度。

结合部;频响函数;参数辨识

对结构进行动态分析时，结合部的影响不可忽略。许多研究表明:结合部处的总柔度占机床总柔度的60%［1］;机床上出现振动问题有60%以上是源自结合部［2］;结合部的阻尼占机床总阻尼的 90%以上［3］。这些结论说明，建立准确的结构动力学模型关键在于能否获得合理的结合部动力学参数。然而，影响结合部动态特性的因素很多，且比较复杂，很多学者已开展了大量的实验和理论研究，但仍有很多问题没有得到根本性的解决，成为制约整机结构动静态特性建模、工程分析计算与优化的一个瓶颈。所以，寻找一种比较合理的结合部动态参数辨识方法，以获得比较准确的结构边界条件，是进一步发展结构动力分析与动态优化设计的先决条件，是机械动力学由单件分析走向整机分析所要解决的关键问题。

近年来，国内外学者已提出了许多辨识方法［4－12］，总体可分为两种，一种是基于模型的辨识方法［4－7］，通过研究实验数据和通过有限元法建立的理论模型相结合去辨识结合部参数。但是，结构的阻尼特性一般很难通过有限元方法准确获得，这为结合部的辨识带来了难度。另一种是基于纯实验的辨识方法［8－12］，通过实验数据去辨识结合部参数。这种方法最大的缺陷是，测量时随机噪声不可避免。随机噪声的存在，使得结合部的辨识变得更加困难。

以国内某龙头企业承担的国家高档数控机床与基础制造装备重大专项产品为研究与应用对象，与国家高档数控机床重大专项产品对接，在综合前人研究成果的基础上，假设结合部一端为固定刚体(图1)，采用频响函数辨识机械结合部刚度与阻尼参数的方法，对实验中能否获取完备频响函数进行了研究。在辨识过程中避开了对频响函数直接求逆，保证了数值计算的稳定，其结果表明该方法具有很高的辨识精度。

1 识别原理

1.1 结合部动态参数与频响函数的关系

机床中常见结合部一般可以用如图1所示的动力学模型表示，即假定结构一端被完全固定，另一端A自由，结合面处采用线性弹簧和阻尼器来模拟其特性。辨识的主要任务是要确定图中刚度与阻尼参数。

子结构〛A在未联接的情况下，动力学方程可表示为:

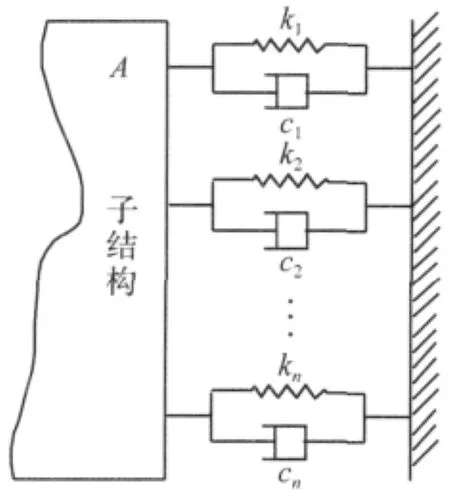
图1 结合部模型Fig.1 Structure connected with joints

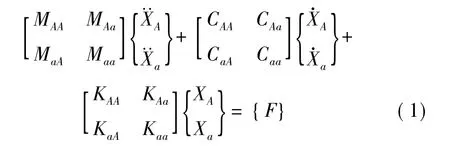
式中:M为结构A的质量矩阵;C为结构A的阻尼矩阵;K为结构A的刚度矩阵;F为结构A的力向量阵;Xa为结构A与支承部上假定的弹簧、阻尼器相联的运动坐标(a=1，2，…，n)，即联接坐标;

XA为结构A除去Xa以外的其余运动坐标，即非联接坐标。

这时，结构A在未联接状态下的动刚度Z可表示:

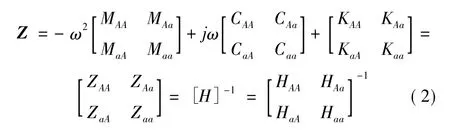
式中H为结构A在自由状态下的频响函数矩阵。

当结构A通过线性弹簧和阻尼联接于某一刚体后，其系统的动刚度～Z为:

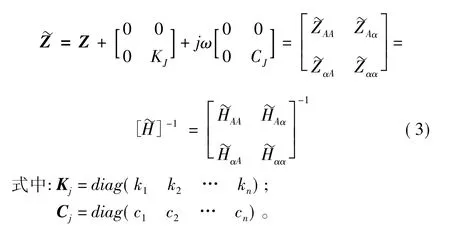
由式(2)与式(3)得:

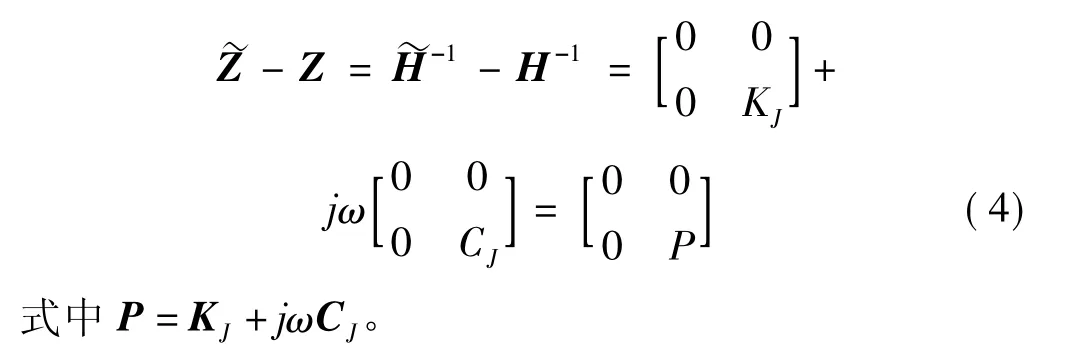
式(4)表达了待识别参数P与频响函数的数学关系。显然，按上式识别不仅需要全部的H和，而且需要对H和矩阵求逆。

为避免直接对矩阵求逆，对式(4)两边分别左乘～H、右乘H有:

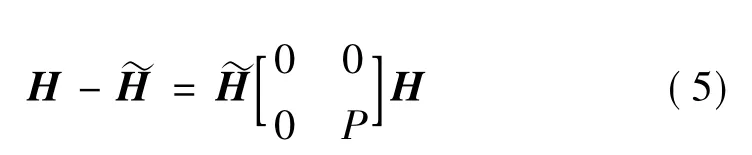
下面根据式(5)建立辨识P的基本公式和辨识结合部刚度与阻尼参数的基本算法。

1.2 基本辨识表达式

假定图1中被联结构在未联与已联状态下，其频响函数H和均由获得。因测试需要，它要求被联结构能从原系统中分离出来，对于不可分离的被联结构必须在组装前对其做未联状态下的激振实验，以便得到矩阵H。

将式(5)按分块矩阵展开并完成矩阵相乘

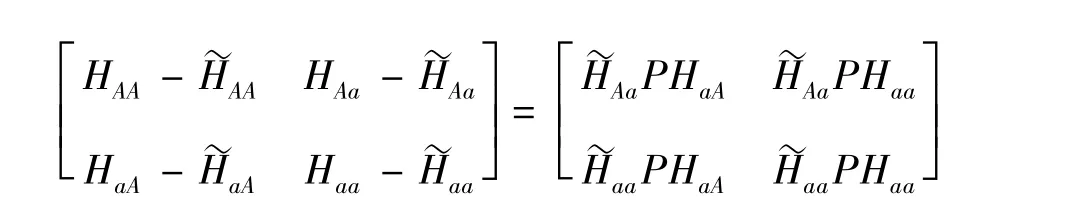
取上式任一分块矩阵对应相等，均可得到求解P的关系式，即:

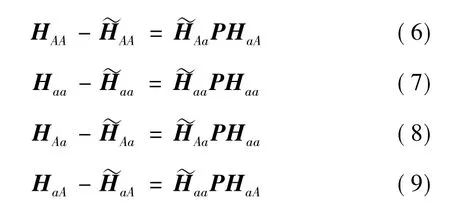
以上四式即为基本辨识公式。

1.3 基本辨识方法

在实际现场测试过程中，由于机械系统的配置，整体工艺的要求等原因，有时不是所有的频响函数都可以通过测试获得。为了使问题变得更加实际可解，本文将对能否获取完备频响函数分别进行了讨论，并作出相应的求解策略。

1.3.1 基于完备频响函数辨识方法

假定被联结构处于未联接状态，联接前后的频响函数矩阵均通过测试获得。由式(7)得:

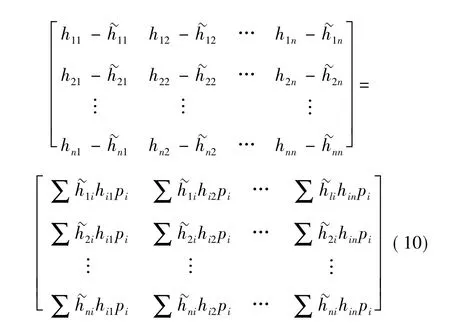
式中右边第l行第m列的元素具有如下形式:

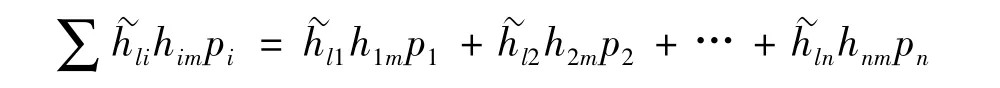
注意，由于频响函数中，原点频响函数比交叉点频响函数可信度高，故取式(10)对角线元素对应相等，可获一组求解pi(i=1，2，…，n)的线性方程组

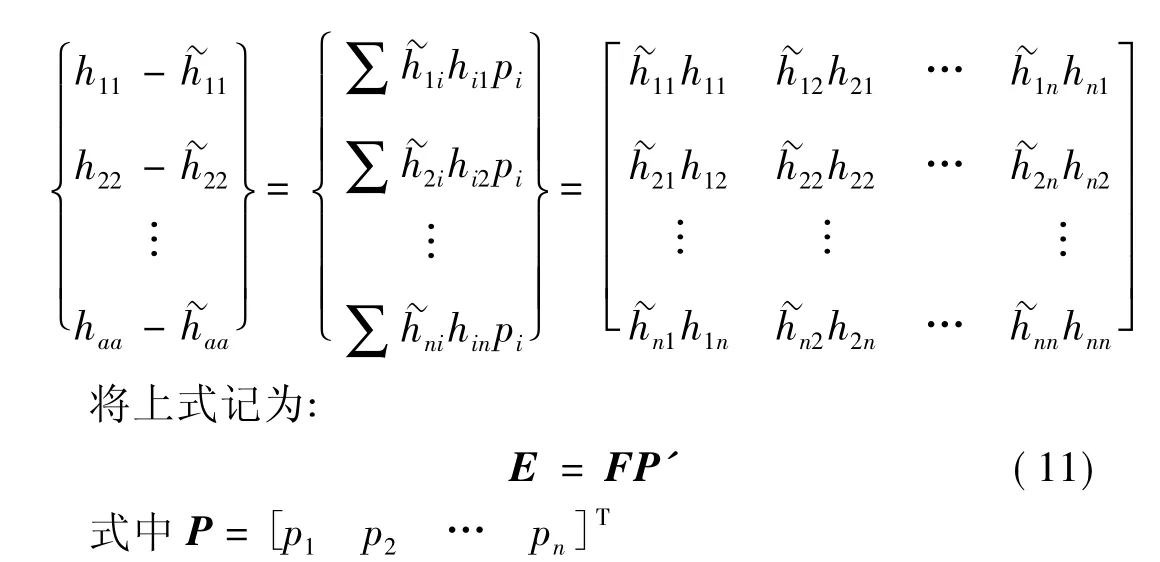
注意到上式是一组复数域线性方程组，设ER、EI分别为E的实、虚部，ER、EI分别为F的实、虚部，又已知P的实虚部分别为K'J与jωC'J，按实、虚部对应相等的原则，上式又可表示为:

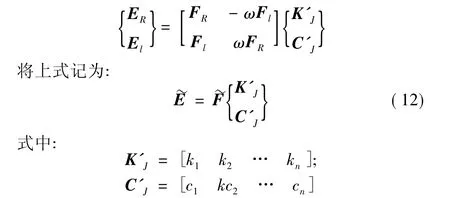
式(12)即为一组求解K'J、C'J的实线性方程组。

同样，因频响函数采样频率ω可以很多，故求解K'J、C'J的方程也很多，设ω有m个，则由式(12)有:

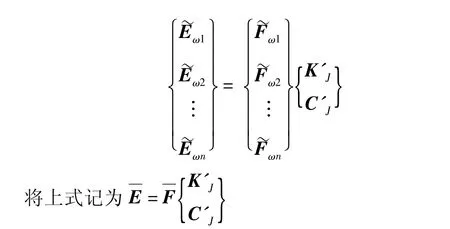
上式为一组矛盾方程，由最小二乘原理将其转化为定解方程:

采用高斯列主元素法解上式，即可辨识出K'J、C'J。

一般来说按式(13)辨识的K'J是有相当精度的，但C'J的精度可能要差些，特别是K'J比C'J在量级上大得较多时更是如此，这主要是因为频响函数中阻尼的信息往往较刚度信息弱。为了更准确地辨识出阻尼，这里建议对阻尼进行二次辨识。重新回到式(11)，并将已辨识的K'J代入式(11)，得:

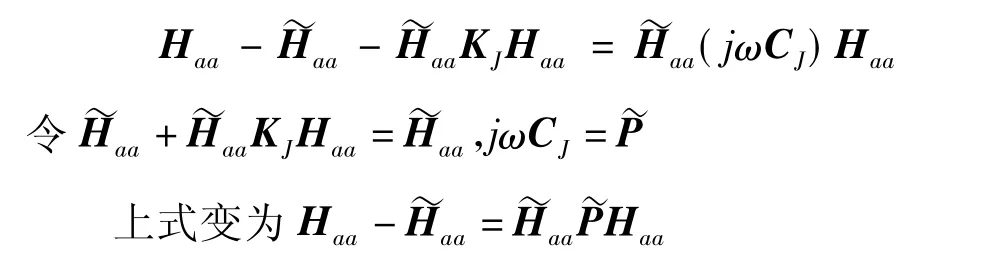
然后仿照前面的方法即可再单独辨识C'J。

1.3.2 基于不完备频响函数的辨识方法

首先假定被联结构在已联与未联两种状态下，所有非联接坐标点均为可测点，即AA与HAA各元素全可测;另外，注意到(1)的定义，只要我们假定的弹簧、阻尼器不安排在转角等难测自由度上，则未联状态下与各联接坐标相关的频响函数Haa与HAa总是可测的，但已联状态下频响函数aa与Aa(或HaA)中可能存在部分难测元素。这时，对难测的部分矩阵元素采用如下公式计算。

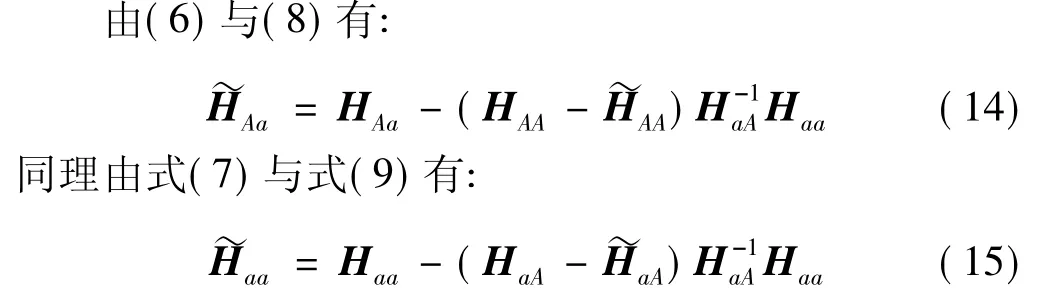
式(14)与式(15)即为补充公式，具体补充方法如下:

2 算例

结合工程实际，以图2所示常见模型为分析模型来说明本文方法的实施过程。假定被连接结构在未联与已联状态下均没有建立有限元模型，其频响函数已知，即所有参数为已知:

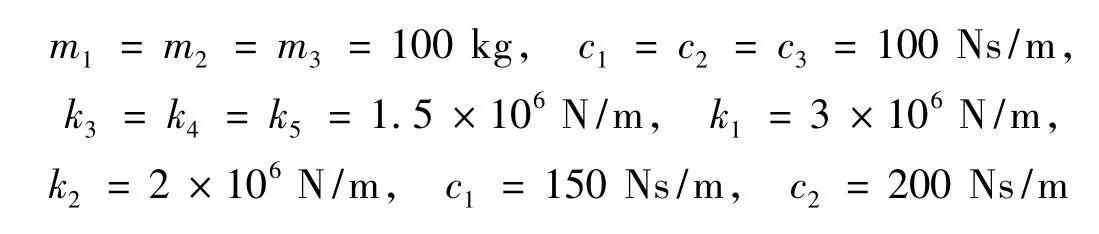
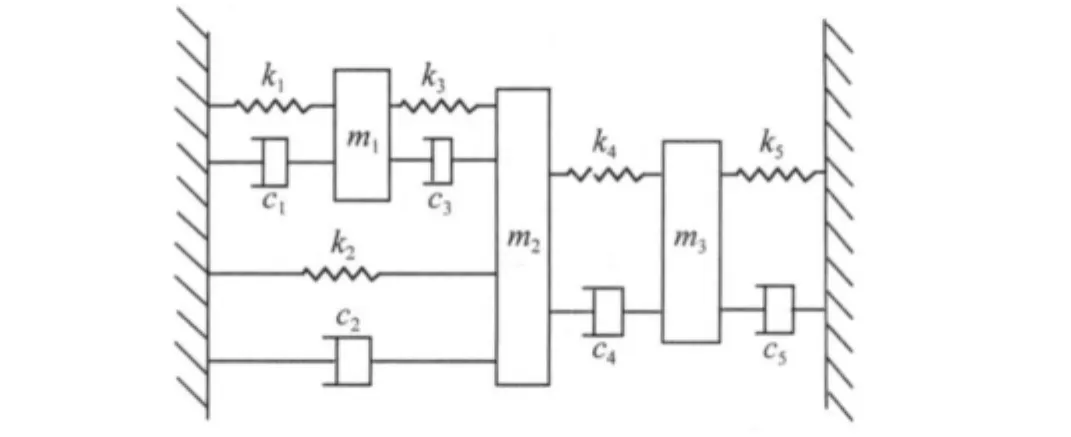
图2 实例系统Fig.2 example of the system

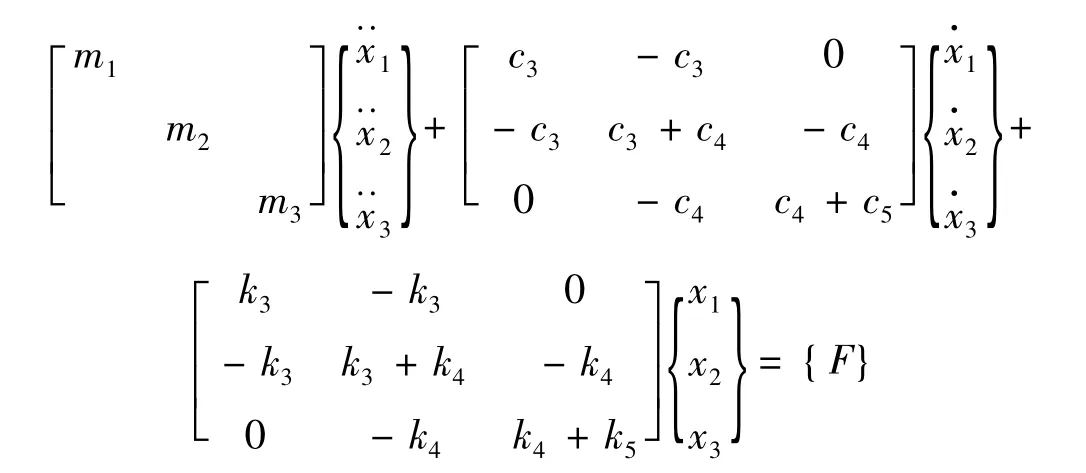
待识别的参数为 k1、k2和 c1、c2。

则 k1、k2、c1、c2未联接时的动力学方程为:

而系统在已联状态下的动力学方程为:

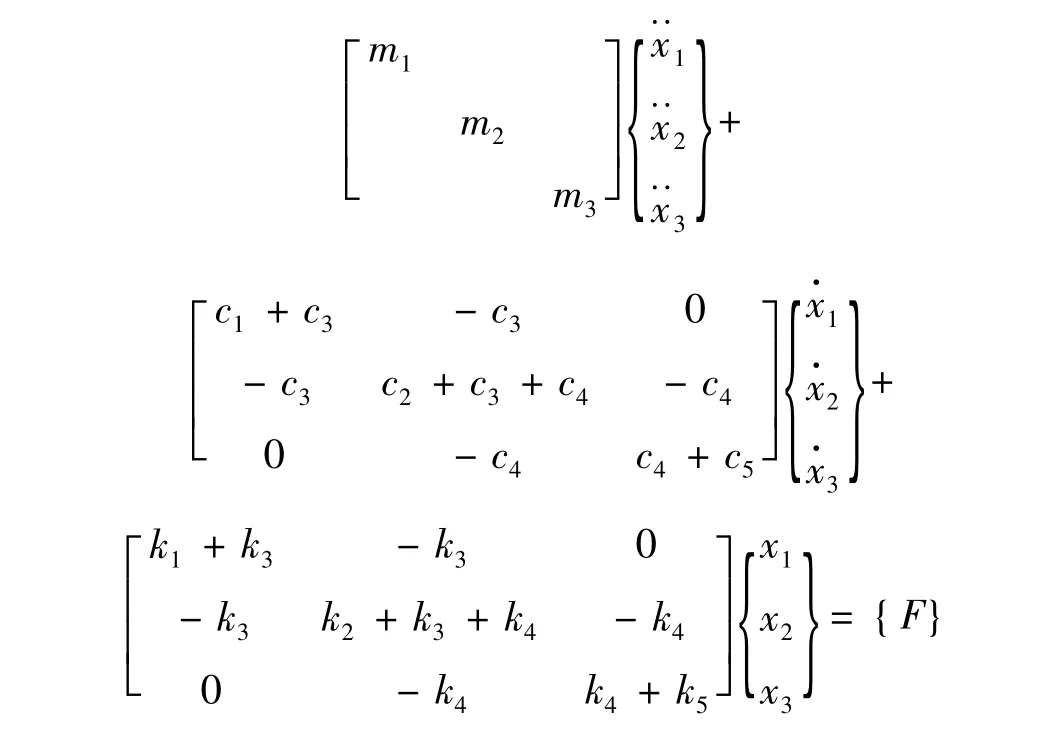
由两种状态下的运动方程，在给定的测试采样频率下可计算出系统准确的Z、与H。本例采样频率ω取100个，频率范围为5 Hz～500 Hz，对未知系统，可根据联接状态下系统的几阶主要低频固有频率来确定测试频带范围，且建议采样点固有频率附近多取些，这有利于反映结构的真实动态特性。为仿真计算，先对本例系统H、的理论值添加一定水平的随机误差，将其作为频响函数，本例添加的误差水平对原点hii、ii与跨点hijij(i≠j)分别控制在5%与6%以内，这比较符合误差分布。同时，对原准确的系统物理参数添加5%左右的随机误差，再形成动刚度矩阵Z。在进行阻尼辨识中，运用了二次辨识的方法，辨识结果如表1误差在8.7%以内，表明采用该方法是行之有效的。

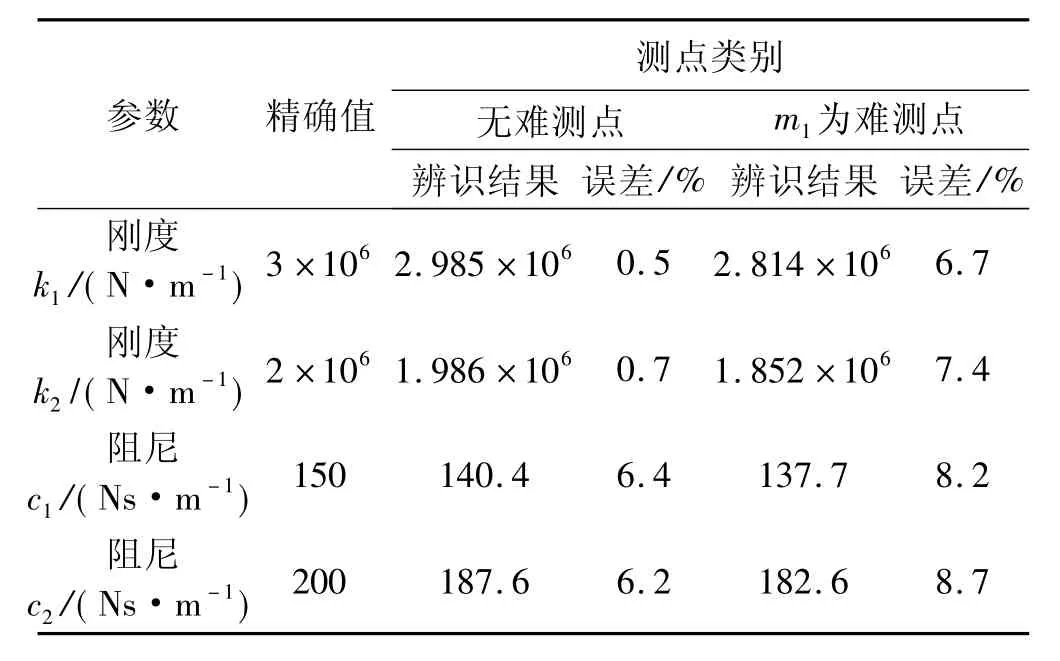
表1 仿真实例辨识结果Tab.1 Identification results of simulation example

3 结论

(1)本文应用了基于频响函数辨识结合部刚度与阻尼的方法，对能否获取完备频响函数分别进行了研究，并作出相应的求解策略。辨识过程避免了对频响函数矩阵求逆运算，且利用的是较低维矩阵关系，从而提高了辨识精度。

(2)文章是以结合部一端为固定刚体为前提，而进行的辨识分析，故在采用该方法时，应将一端固定。但如果两端均不能固定，则应分别建立两部件在自由状态的有限元模型，或分别对两部件在自由状态下测试其频响函数，再在整体状态下测试频响函数，仿照本文原理，可导出类似的辨识公式。

(3)采用本文的辨识方法可进行系列化实验研究，以获得可供实用的经验公式与图表。并将辨识得到的结合部等效动力学参数，一方面可以判定结合部等效刚度和阻尼的特性及其随外加载荷作用的变化规律;另一方面可获得典型工况下结合部完整的动力学模型，为动力分析、动力修改及动态优化设计奠定基础，为产品的快速数字化设计提供理论与技术支持。

［1］Connolly R，Thomley R H.The Significance of Joint on the Overall Deflection of Machine Tool Structures 6thMTDR Conf，1965.

［2］Burdekin M，Baek N A.Cowley.Analysis of the local deformation in machine joints［J］.Mech.Eng.Sci，1979，34(3):15－17.

［3］Vafaei S，Rahnejat H，Aini R.Vibration monitoring of high speed spindlesusingspectralanalysistechniques［J］Machine Tools＆ Manufacture，2002，42:1223－1234.

［4］Nalitolela N G.A.Mass or Stiffness Addition Technique for Structure Parameter Updating［J］.The International Journal of Analytical and Experimental Modal Analysis.1992，7(3):157－168.

［5］HjelmstadK， MutualD. ResidualEnergyMethodfor Parameter Estimation in Structures［J］.Journal of Structural Engineering，1992，118(1):223 －242.

［6］李润方，韩 西，等.齿轮传动系统结合部动力学参数识别［J］.中国机械工程.2001，12(12):1333－1335.

［7］廖伯瑜，周新民，尹志宏.现代机械动力学及其工程应用［M］.机械工业出版社.2004.

［8］Liu W，Ewins D J.Substructure synthesis via elastic media［J］.Journal of Sound and Vibration，2002，257(2):361－379.

［9］Damjan C，Miha B.Identification of the dynamic properties of joints using frequency-response functions［J］.Journal of Sound and Vibration，2008，317(1－2):158－174.

［10］ Mascardelli B A.Park S S，Freiheit T.Substructure coupling of micro end mills to aid in the suppression of chatter［J］.Journal of Manufacturing Science and Engineering，Transactionsofthe ASME， 2008， 130(l)0110101－01101012.

［11］ Ren Y，Beards C F.Identification of Effective'Linear Joints Using Coupling and Joint Identification Techniques［J］.Journal of Vibration and Acoustics.1998，120，331 －338.

［12］ Wang J H.Identification of Parameters of Structural Joints by Use of Noise Contaminated FRFS［J］.Journal of Sound and Vibration，1990，142:261 －277.

Identifying mechanical joint dynamic parameters based on measured frequency response functions

GUO Tie-neng，LI Ling，CAI Li-gang，LIU Zhi-feng，ZHAO Yong-sheng，Yang Kun

(College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Beijing，100124，China)

In order to obtain a more accurate boundary condition of structure in dynamic analysis and optimization design，the joint parameter identification is one of the key technologs.In combination with engineering practice，the method based on frequency response function(FRF)to identify the characteristic parameters of the joint was proposed.Whether the complete FRF can be obtained or not was studied and the corresponding solving strategy was presented.The method avoids the matrix inversion directly，and transforms contradictory equation to equation with definite solution by using least-square principle，which ensures the stability of numerical calculation.Considering the damping information is inferior to stiffness information in identification process，in order to identify the damping parameter more accurately，a successive identification method was further proposed.Example analysis confirms that the method is of high identification accuracy.

joint;frequency response function;parameters identification

TH113;TH123

A

国家重大专项(2009ZX04014－033);国家自然科学基金(50905004)

2010－03－15 修改稿收到日期:2010－04－12

郭铁能 男，博士，讲师，1975年5月生

李 玲 男，博士生，1981年7月生