结构损伤识别的混合神经网络方法

刘石 佴磊

结构损伤识别的混合神经网络方法

刘石 佴磊

在损伤位置和程度的诊断中分别构造各自相适当的网络和识别样本形成混合神经网络系统,并选择不同的输入参数对结构损伤的位置和程度进行了识别,针对一个损伤钢梁进行了数值仿真,从而证明了混合神经网络两步检测法的可行性。

混合神经网络,频率变化比,残余力向量,损伤定位,损伤程度

目前在结构损伤识别的研究中,大多采用一步直接诊断方法,即同时判别损伤的位置和程度。这种方法在识别简单结构时是十分有效的,但是大部分需要进行损伤诊断的结构都比较复杂,其构件数目和动力自由度数目巨大,对数据采集精度要求较高,需要耗费较长的时间和较多的计算机资源进行计算和分析,尤其是结构健康监测系统,采集数据和分析数据的周期相对较短,当采用此方法时更为不利。因此本文采用了一种两步诊断方法,先判别结构损伤部位,然后具体诊断损伤部位的损伤程度。

在训练网络样本数量有限的情况下,结构损伤定位是比较容易实现的,对网络的性能和数据的要求较低,而结构损伤程度的判定受样本完备性、网络性能、噪声影响较大。考虑系统资源、算法耗时、所用数据等因素,本文在判别结构损伤部位时使用 BP网络,在诊断结构损伤程度时使用径向基函数网络。

采用什么参数作为神经网络的输入向量最为合适是利用人工神经网络进行结构损伤检测的关键问题,神经网络输入参数的选择及其表达形式直接影响结构损伤检测的结果,可选择的动力参数有很多：固有频率、位移或应变模态(振型)、频响函数、加速度响应等。对结构损伤敏感程度由高到低依次为：应变频响函数指标、曲率/应变模态指标、位移频响函数指标、固有频率指标、位移模态指标。有些特征参数在用来进行损伤定位时,往往与损伤程度有一定关系,严重影响了损伤定位的精度。与损伤程度无关,仅是损伤位置的输入特征参数有归一后的频率变化比、损伤信号指标等,频率的测量最为简单易行,精度也比较高,因此选择频率的变化率作为结构损伤定位中网络的输入参数。由于自振频率对损伤程度不敏感,而损伤发生后,频率和振型都发生变化,所以由两者的变化得到的残余力向量作为判定损伤程度的网络输入参数。

通过以上分析,本文设计了一种两步结构损伤诊断方法,即混合神经网络方法,其原理如下。

1 结构损伤位置的初步诊断

1.1 参数选择：标准化的频率变化率

结构振动的特征值问题由动力学方程描述：

其中,K,M分别为整体刚度矩阵和质量矩阵;φ为正则化振型;ω为固有频率。

损伤后结构运动方程为：

其中,ΔK,ΔM和 Δφ分别为整体刚度矩阵、质量矩阵和振型的改变量。结构损伤通常不会影响结构的质量特性,ΔM可以看作等于零。展开式(2)且忽略二阶项,得：

由此可见,结构的任意阶频率变化均包含了相同的单元损伤程度信息。因此,引用结构的低阶固有频率变化量作为判断结构损伤的特征向量在理论上是可行的,且结构的自振频率测试精度较高。将频率变化率标准化作为网络的输入参数：

其中,Wui为结构损伤时的固有频率;Wdi为结构完好时的固有频率;Wmax为最大的固有频率。

1.2 网络选择：BP神经网络

BP模型的主要思路是输入样本为x,实际输出为y,而目标输出为 t,通过调整权值和阈值使 y和 t尽可能地接近,即使网络输出层的误差平方和最小,是一种有导师的学习算法,仅含一个隐含层,输入神经元有 n个,隐含层神经元有s个,激活函数为 fj,输出层有m个神经元,对应的激活函数为fk,输出为Y,目标矢量为T,则隐含层中第 j个神经元的输出为：

其中,yj为节点 j的输出;ωji为节点之间的连接权值;bj为阈值,而输出层第k个神经元的输出为：

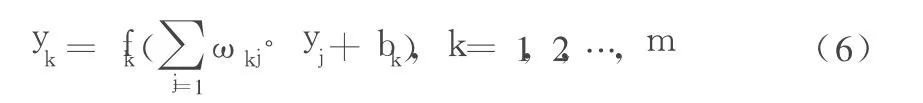
定义误差函数为：

其中,tk为期望输出。

则输出层的权值变化为：其中,η为学习速率,用来调整网络的收敛速度。实践表明,η通常取一接近 1的数。而 δkj=(tk-yk)f′,f′为激活函数的导数。α为动量因子,用来传递上一次权值变化的影响。

2 损伤程度的诊断

2.1 参数选择：残余力向量

残余力向量可利用结构破损前的质量刚度矩阵及少量低阶模态参数求得。

结构破损后其固有频率与振型将要产生变化,则动力方程右端项不再为零,即：

其中,d为残余力向量,对于前 l阶固有频率与振型由式(9)得到残余力矩阵 Dl,矩阵Dl的第 i行元素绝对值最大值用 β表示,即：

其中,dij为矩阵 Dl的 i行 j列元素。

2.2 网络选择：径向基神经网络

径向基神经网络由含有径向基函数神经元的隐层和含有线性神经元的输出层组成。隐层中每一个神经元中心及涵盖域决定了径向基函数的位置和宽度。输出层神经元将对隐层神经元节点输出进行加权叠加。理论证明：一个三层径向基函数可以拟合任意函数。

在径向基网络中,隐层神经元特性可用高斯函数描述为：

其中,β为分布常数。由高斯函数对输入信号在局部产生响应的特点可以在学习过程中获得较高的速度。

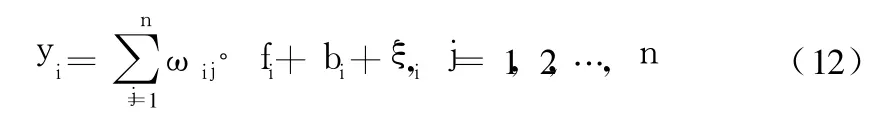
3 结构损伤识别数值模拟

分析采用简支矩形钢梁模型如图 1所示。钢杆直径 30mm,材料基本参数如下：弹性模量 E=2.06 MPa,材料质量密度为7 800 kg/cm3,采用减小截面的方法来模拟损伤,模拟损伤处沿纵向宽 30mm,利用ANSYS建模分析得到结构前四阶频率和振型。

样本构造：在 A,B,C,D,E五部位处模拟损伤,每个部位都考虑八种损伤程度,10%,20%,30%,40%,50%,60%,70%,80%,只考虑单位置损伤和两个位置同时损伤的情况,再加上结构完好情况,共形成 681种不同损伤情况的组合,由于 BP网络和径向基函数网络使用的输入参数不同,所以每个网络各构造样本 681组,抽取 5组样本作为测试样本,其余送入网络进行训练。

构造BP网络结构为 4—12—5,4个输入单元对应频率的四阶变化率,隐含层的选取经试算在取 12时网络收敛速度最快,5个输出单元对应 5个部位的损伤。径向基函数网络输入层和输出层的选取和 BP网络相同。网络诊断结构见表 1,表 2。

表1 BP网络损伤位置识别结果

表2 径向基函数网络损伤位置识别结果

4 结语

1)在训练网络时,相同的样本数目,BP网络经过 1 272次达到收敛,径向基函数网络经过 261次达到收敛,虽然输入参数并不是同一样本,但是从中也可看出径向基函数网络的性能要优于BP网络。2)算例中只采用了前四阶频率和振型信息,但是取得了较好的识别效果,这说明频率变化比对损伤位置较为敏感,而残余力向量对局部损伤较为敏感,适合作为分步损伤识别的输入参数。但是频率对称结构的损伤不够敏感,在损伤定位时,对称部位只能归入同一类别。3)该算例证明采用本文提出的混合神经网络两步检测法是可行的,并取得了较好的识别效果。但是该算例较简单,没有考虑噪声对样本的影响,使用该方法进行复杂结构的损伤识别尚需进一步研究和试验论证。

[1]董 聪.现代结构系统可靠性理论及其应用[M].北京：科学出版社,2001.

[2]陈 伟,瞿伟廉.人工神经网络技术在结构损伤诊断中的应用[J].世界地震工程,2002,18(2)：20-21.

[3]瞿伟廉,黄东梅.高耸塔架结构节点损伤基于神经网络的两步诊断法[J].地震工程与工程振动,2003,23(2)：44-45.

[4]王柏生,倪一清,高赞明.框架结构连接损伤识别神经网络输入参数的确定[J].振动工程学报,2000,13(1)：66-67.

[5]刘 箴,唐岱新.建筑结构损伤诊断方法研究[J].哈尔滨建筑大学学报,2000,33(1)：73-74.

[6]陈长征,王占国,罗跃纲.钢梁损伤的神经网络诊断分析[J].工业建筑,2002,32(1)：55-56.

On hybrid neuralnetwork method for structural damage identification

LIU Shi NAILei

The paper establishes the respectively suitable network and the identification samples to thehybrid neuralnetwork system from the diagnosis for damage position and the levels,selects the various inputparameter to identify the structural damage position and the levels,and undertakes the numerical simu lation for the damaged steelbeam,so as to prove the feasibility of the hybrid neural network two-step checkingmethod.

hybrid neural network,frequency change square ratio,residual force vector,damage location,damage level

TU317

A

1009-6825(2011)03-0021-02

2010-09-22

刘 石(1980-),男,吉林大学建设工程学院博士研究生,吉林 长春 130026

佴 磊(1967-),男,博士生导师,教授,吉林大学建设工程学院,吉林 长春 130026