分析系统参数对海底输流管道极限跨长的影响

吴 卫， 包日东， 蔡仕卿， 关玲玲

(1.沈阳化工大学机械工程学院，辽宁沈阳110142; 2.辽宁东油建设监理公司，辽宁沈阳110031)

随着世界陆地上油气资源的日益减少，海洋能源的开发变得越来越重要，海底输流管道则成为海洋到陆地上最快捷、经济、可靠的运输方式.然而海底管道在海底地震，海流对海床的长期冲击以及管道内流引起的管道振动都会使海底管道产生悬跨现象.当海水流经管道的悬跨段时就会产生周期性的涡激振动，当涡激振动频率达到管道固有频率时管道就会发生共振，共振是海底管道疲劳失效的主要原因.长期的涡激振动会缩短管道寿命，甚至会造成海洋污染，次生危机等一系列问题.因此，研究海底输流管道的极限跨长，对于海底管线的安全性具有重要意义.

对于海底输流管道极限跨长的研究，国内外作者做了大量实验研究［1－2］.Holmes［3］证明了理想支承的管道在定常流作用下不会发生颤振失稳.以往学者通常在两端简支或固支情况下进行实验研究［4－5］，但工程中的支承情况与理想支撑存在较大差异.为更加接近工程实际，本文将海底管道悬跨段处理成两端一般支承的模型，其弹性支承系数根据各地管线埋土的实际情况测量选取，或采用相应的方法来确定，如文献［6］基于模糊推理规则，提出确定支撑土壤的弹性系数和阻尼系数的方法，这样的分析结果与实际更接近.在此模型基础上，本文利用工程振动的理论和方法，以不发生共振现象为控制条件，计算允许的管跨长度，并重点讨论输流管道的内流，流体密度，管道内部压强，管道外径对管道允许跨长的影响.

1 数学模型

研究埋设于海底的悬跨管道，截面为均匀圆环形，悬空段长度为l，悬空段两端视为一般支承.管内流体相对于管壁的流速为U，管内流体的相对压强为p，两端轴向拉力为T，来流速度为V.建立海底输流管道的悬空段示意图如图1(a)所示，简化成一般支承梁模型示意图如图1(b)所示，图1(b)中k1，k2为悬跨管道竖直方向的弹性支撑系数，kT1，kT2为扭转支撑弹簧系数.此建模过程中只研究管道在竖直方向的平面问题.

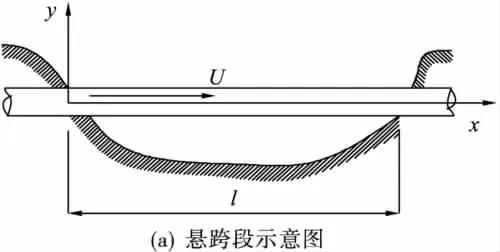
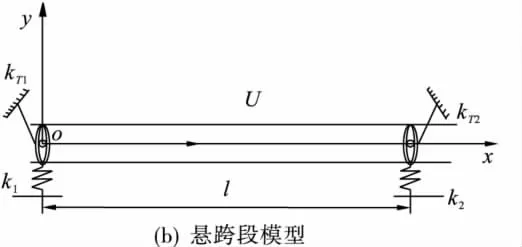
图1 输流管道悬跨段示意图Fig.1 Schematic of free span pipeline

1.1 运动方程

图1(b)所示的模型管道，对管道微元和管内流体微元运用达朗伯原理，可得Kelvin-Voigt黏弹性管道两端受扭转弹簧和线性弹簧约束下的竖向运动微分方程［7－9］.

两端一般支承的边界条件为:

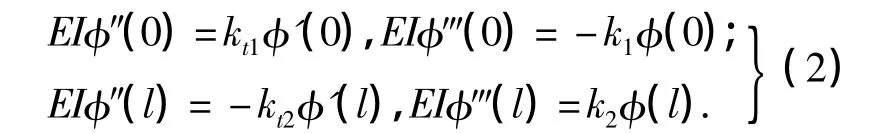
式(1)中，mf为流体线密度，mp为管道线密度，ma为外流作用在管道上附加线密度，a为Kelvin-Voigt黏弹性系数，Cf为流体阻尼系数，U为管内流体速度，EI为管道上的抗弯刚度，p为管内相对压强，Af为管道内流体的过流断面积，T为管道轴向力，Fl为升力、Ff为浮力，g为重力加速度，υ为泊松比(取0.3).

管外流体附加质量为

式(3)中Cm为附加质量系数，D为管道外径，ρc为管外流体密度.

管外流体产生的升力为

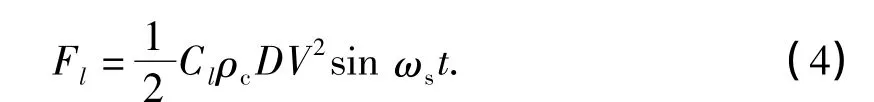
式(4)中Cl为升力系数(可取为0.5～1.5)，V为管外流体流速，ωs为涡激频率，即Strouhal频率，其计算公式为

式(5)中的Sr为数Strouhal，根据20℃时水的黏性系数计算出雷诺数Re，再由Sr与Re的关系取Sr=0.22.

对于流体阻尼系数Cf［10］，取

式中CD为拽力系数，对于雷诺数Re＜3×105时，取CD=1.2.

单位管长上外流产生的浮力为

式(7)中Ae为管道外横截面积.

将式(3)～式(7)代入方程(1)可得

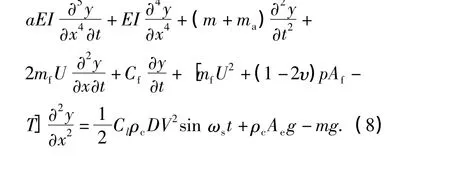
1.2 微分求积法模拟方程

引入如下的无量纲量:

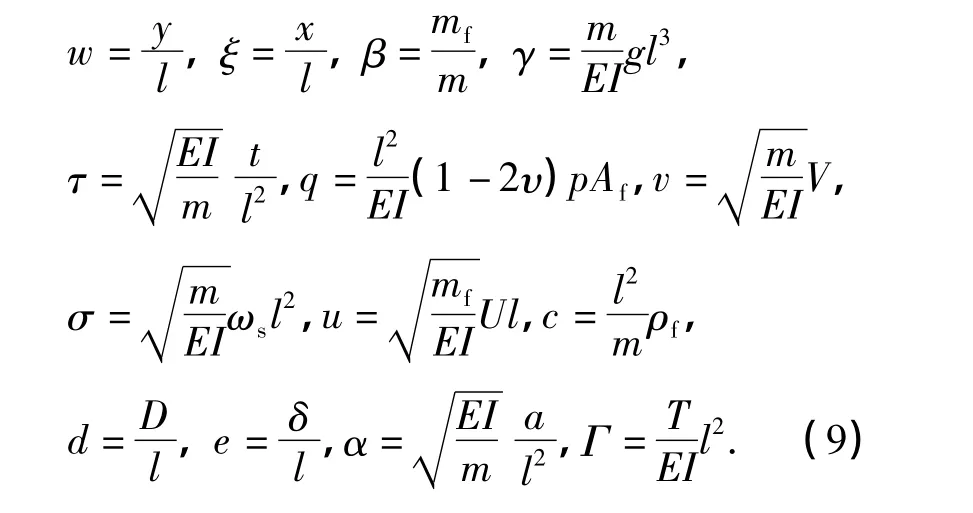
将方程(8)化为无量纲形式:

设方程(10)的解为

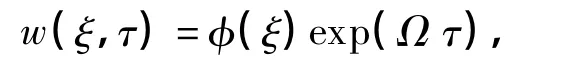
则方程(10)化为

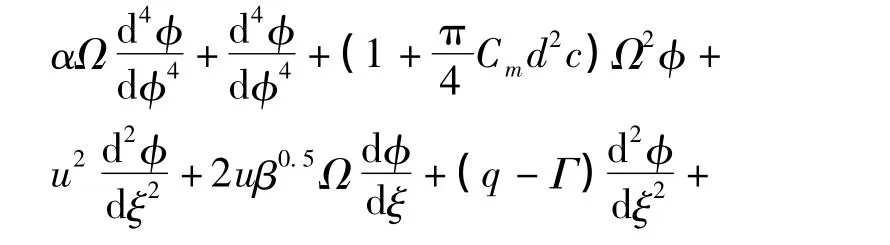
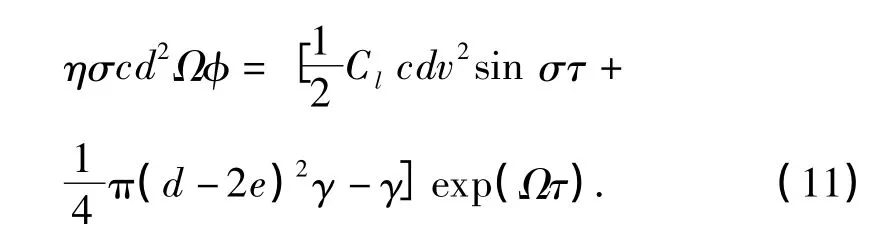
边界条件化为

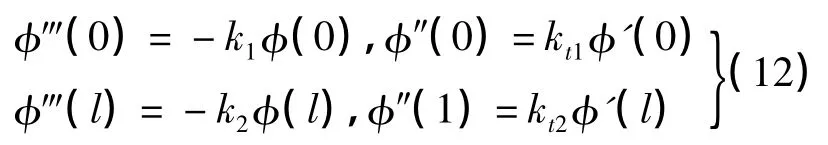
用微分求积法得到悬跨管道的DQ法模拟方程和相应的边界条件为

用下标b表示边界上的量，d表示非边界上的量，即

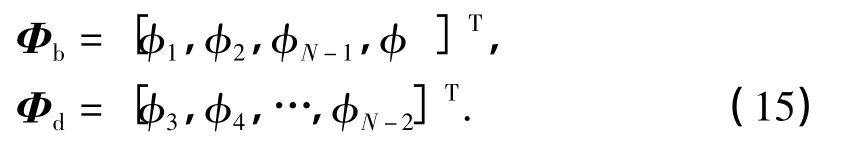
将模拟方程(13)和边界条件式(14)写成矩阵形式为

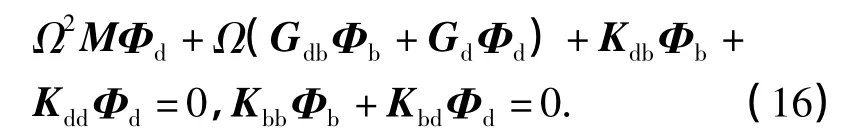
矩阵方程(16)中各子矩阵的元素可从式(13)和(14)得到.由式(16)消去Φb后可得到

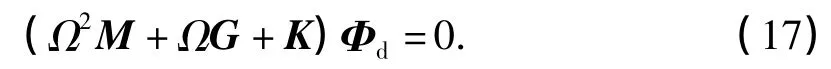
式中，

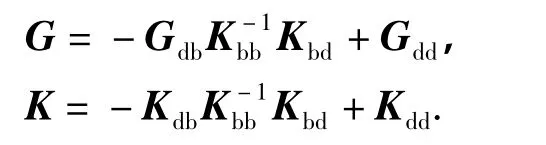
由于流速导致陀螺力的作用，Ω一般为复数，其虚部Im(Ω)表示输流管的无量纲自振频率，式中G为陀螺力，K为刚度阵，G和K中含有流速v和u及质量比β等参数.方程(17)构成广义特征值问题，固定某些参数，令其一参数变化可得出此参数对输流管道固有频率的影响情况，当管道的固有频率与管道的尾流旋涡释放频率接近［11］(ω1=(0.7～1.3)ωs)时，管道发生锁振现象，把此时的管长作为悬跨管的允许跨长.

2 算例分析

在计算管跨长度时，采用表1所示的系统参数，用MATLAB编程计算.

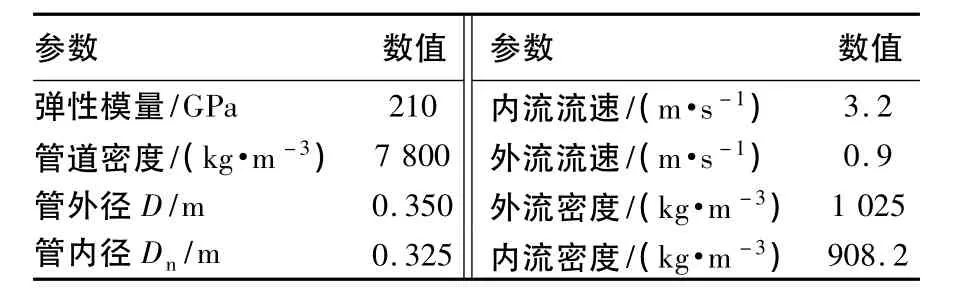
表1 输流管计算参数Table 1 Calculating parameters of the pipeline

在计算过程中，讨论某一参数对管道跨长的影响时，则此参数取变化的数值，管跨两端的土弹簧刚度取k1=k2=kt1=kt2=50和k1=k2=kt1=kt2=100时进行对比，计算结果如图2～图6所示.

2.1 弹性系数及管内流速对极限跨长的影响

图2为悬跨管道两端弹性系数变化时其极限跨长变化曲线.模拟管道为两端一般支承海底管道，选取两端弹性支承对称相等进行模拟分析.

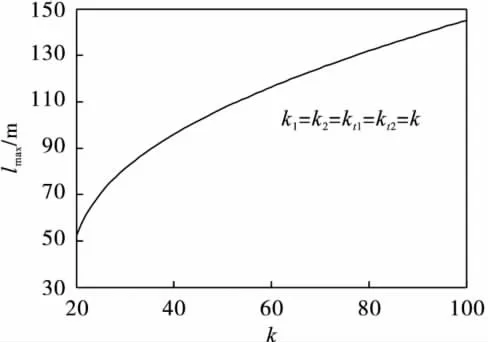
图2 悬跨管道的极限跨长随两端弹性系数的变化Fig.2 Variation of span limit with elastic coefficient at ends

从图2可知:管道的极限跨长随弹性系数的增大而增大，在弹性系数较小时增长较快，弹性系数较大时增长平缓.

图3为悬跨管道的极限跨长和管内流速的变化规律.从图3可以看出:在海底管道两端一般支承的情况下，管跨的极限跨长呈下降趋势，且随着弹性系数的增大极限跨长增大.这是由于在管内流体的耦合作用和一定的管跨端部支承刚度下管跨段的固有频率下降，但固有频率又随管跨端部支承刚度的增大而增大的原故.

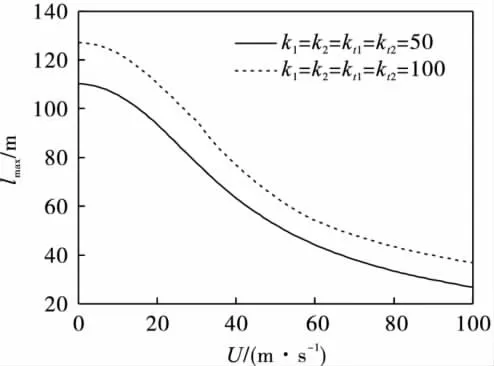
图3 悬跨管道的极限跨长随管内流速的变化Fig.3 Variation of span limit with flowrate inside pipeline

2.2 管内压强对极限跨长的影响

图4为悬跨管道的极限跨长随管道内流体压强的变化规律曲线.从图4可以看出:2种弹性刚度下管跨的极限跨长随管内流体压强的增大而减小.这是因为管内流体压强通过弹性管道的泊松耦合效应影响到管跨的固有频率特性，使管跨段的固有频率下降而导致极限跨长下降的原故.从图4可以看出:压强在0～15 MPa区间内，由于管道内外压强差太大使管道的跨长急剧下降，尔后，极限跨长的下降幅值趋于平缓.

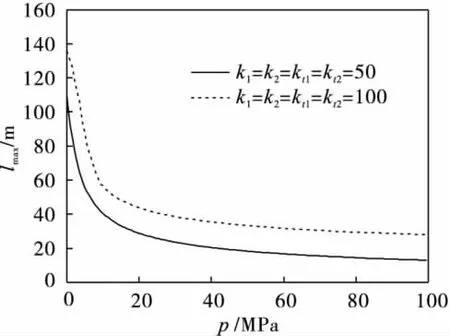
图4 悬跨管道的极限跨长随管内流体压力的变化Fig.4 Variation of span limit with fluid pressure inside pipeline

2.3 管道外径和流体密度对管跨长度的影响

图5和图6分别为悬跨管道的极限跨长随管道外径和管内所输送流体密度的变化曲线.从图5和图6可以看出:极限跨长随管跨外径和所输送流体密度的增大而增大，但流体密度对极限跨长的影响相对较小.管道外径改变时，会影响到管外流体产生的浮力、附加质量力、升力、阻尼力和涡激频率，它对管跨固有频率的影响较复杂.输送流体密度的改变则改变了单位管长内流体质量与总质量的比，即方程中的β，但管外流体产生的浮力、附加质量力、升力、阻尼力和涡激频率并未受到影响.从图5、图6还可得出，在相同的管外径或管内流体密度下，随着管跨端部支承刚度系数的增大，其极限跨长增大.

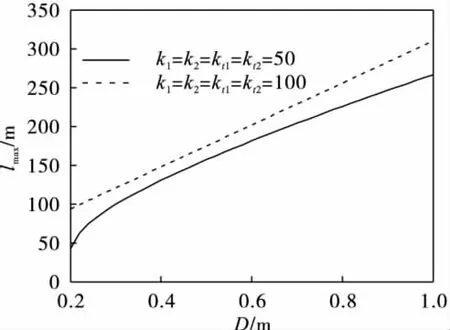
图5 悬跨管道的极限跨长随管道外径D的变化Fig.5 Variation of span limit with diameter outside Pipeline

图6 悬跨管道的极限跨长随管内流体密度的变化Fig.6 Variation of span limit with density of fluid inside pipeline

3 结论

(1)将海底管跨入土端模拟成两端受土弹簧支承和约束的一般支承梁模型，综合考虑管外流体的附加质量力、升力、阻尼力、浮力、管道材料非线性和管截面的轴向力、管内流体的压强、流速、外部流体的涡激作用，建立海底管跨的流固耦合运动方程和DQ法的模拟方程，并进行极限跨长的仿真分析.该方法比将悬跨段管道处理成理想支承的模型更合理，更接近工程实际，能够应用于工程中水下悬跨管道的研究.

(2)从数值仿真结果可以看出:管跨产生锁振的极限跨长随管跨入土端弹簧刚度、管道外径、管内输送流体密度的增大而增大，随管内流体流速、压强的增大而减小.

［1］ 马良.海底管道在水流作用时诱发的振动效应［J］.中国海洋平台，2000，15(2):30－34.

［2］ Choi H S.Free Spanning Analysis of Offshore Pipelines［J］.Ocean Engineering，2001，28(10):1325－1338.

［3］ Holmes P J.Pipes Supported at Both Ends Cannot Flutter［J］.Journal of Applied Mechanics，1978，45 (3):619－622.

［4］ 李昕，刘亚坤，周晶，等.海底悬跨管道动力响应的试验研究和数值模拟［J］.工程力学，2003，20(2): 21－25.

［5］ 周晶，李昕，马恒春，等.地震时海底悬跨管道动力特性试验研究［J］.水利学报，2003，34(1):12－16.

［6］ 余建星，罗延生，杨晶.海底管线悬空段模糊固有频率的计算［J］.地震工程与工程振动，2002，22 (3):66－70.

［7］ 包日东，闻邦椿.水下悬跨管道动力响应分析［J］.振动与冲击，2007，26(8):140－143.

［8］ 包日东，闻邦椿.水下悬跨管道动力稳定性的DQ解法［J］.应用力学学报，2008，24(3):94－98.

［9］ 包日东，闻邦椿.用微分求积法分析不同支承条件下水下输流管道的动力特性与容许悬跨长度［J］.地震工程与工程振动，2009，29(4):131－137.

［10］Facchinetti M L，Langre E de，Biolley F.Coupling of Structure and Wake Oscillators in Vortex-induced Vibrations［J］.Journal of Fluids and Structures，2004，19(2):123－140.

［11］王鑫伟.微分求积法在结构力学中的应用［J］.力学进展，1995，25(2):232－240.