热传导方程几种差分格式的MATLAB数值解法比较

冯立伟

(沈阳化工大学数理系，辽宁沈阳110142)

许多工程问题需要研究热量在物体内部的传导情况或某种物质在液体中的扩散情况，因此研究热传导问题特别是非稳态热传导问题十分重要.目前热传导方程已有多种求解格式［1－2］.MATLAB是目前最流行、应用最广泛的科学和工程计算软件.MATLAB基于矩阵运算，具有强大的数值运算能力和图形可视化能力，是方便实用、功能强大的数学软件［3］.用MATLAB求解常微分方程已有大量的研究［4－6］.王飞等介绍了如何使用MATLAB实现有限差分法求解微分方程［7］.高理平等给出了对两点边值问题有限元方法的程序［8］.李灿等对热传导问题的MATLAB数值计算进行了讨论［9］.本文讨论求解一维热传导方程几种不同差分格式的MATLAB编程方法，并使用算例进行检验和对结果进行分析.

u(x，t)表示在t时刻物体内部坐标为x处的温度，a是热传导系数，f(x，t)为热源.

1 热传导方程差分格式

1.1 差分格式的建立

首先对x-t平面进行网格剖分.分别取h，τ为空间步长与时间步长，用2族平行直线xj= jh，tk=kτ将矩形区域［0，T］×［0，L］分割成矩形网格.

显式格式:

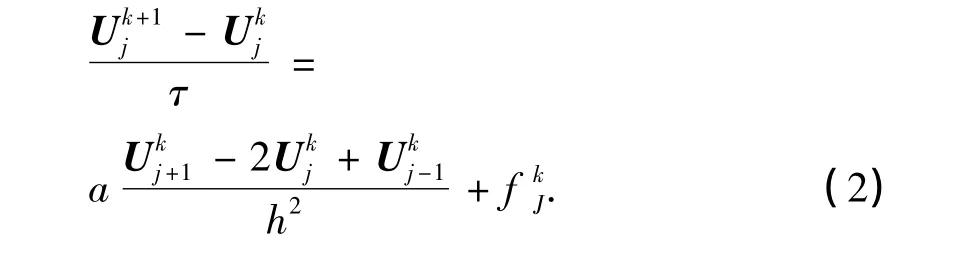
隐式格式:

Crank-Nicolson格式:

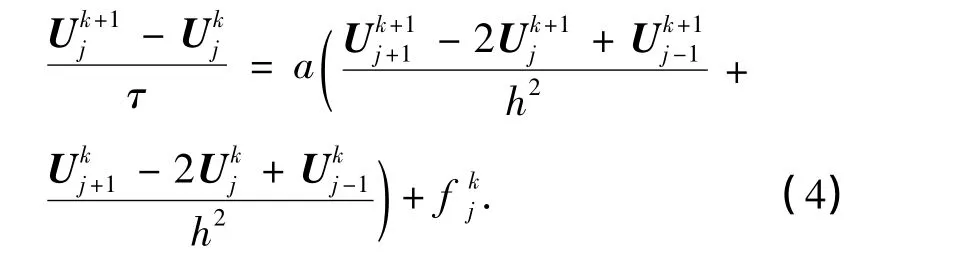
Du Fort Frankel格式:

由Taylor公式容易得出:它们都与一维热传导方程相容，其截断误差分别为O(τ+h2)，O(τ+ h2)，O(τ2+h2)和O(τ2+h2)［1］.

1.2 初、边值条件的处理

对定解条件进行离散化.由初始条件及第一类边界条件，可直接得到:

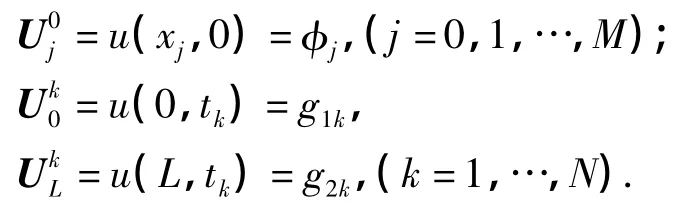
1.3 稳定性分析

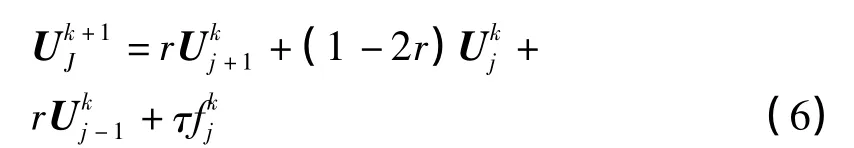
使用Fourier方法可知，当r≤1/2时显式格式稳定.

隐式格式变为:

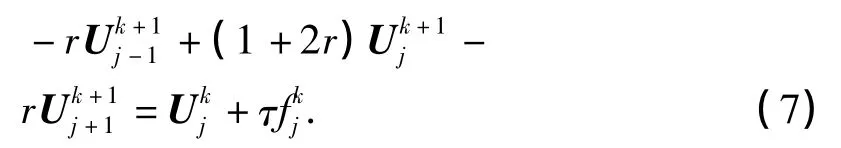
由Fourier方法可得隐式格式恒稳定.

Crank-Nicolson格式变为:

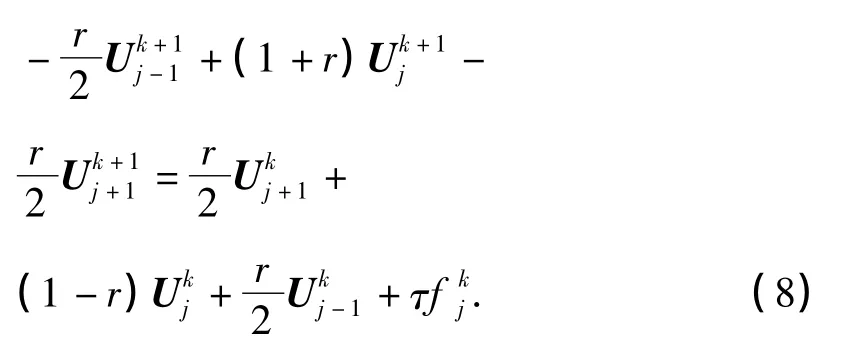
对于r＞0恒有增长因子|G|≤1，恒稳定.

Du Fort Frankel格式变为:

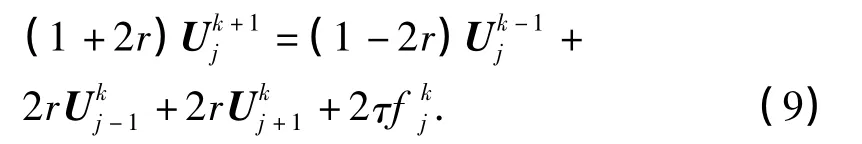
由Fourier方法可得Du Fort Frankel格式恒稳定.

2 差分格式的求解

显式格式:将(6)式与离散化的初边值条件结合，得到求解此问题的差分方程组:

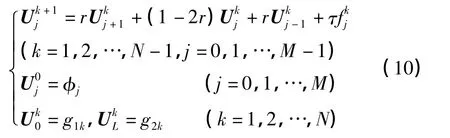
由于初始时间层上的u值为已知，由(10)式即可算出u在第一层各个节点处的近似值u1j.重复使用此式，可以逐层计算出所有的

隐式格式:将(7)式与离散化的初边值条件联立，得差分方程组:

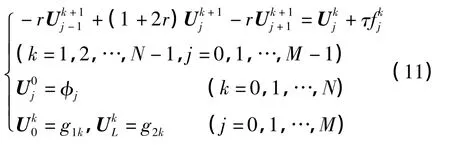
将上述方程组改写成矩阵形式

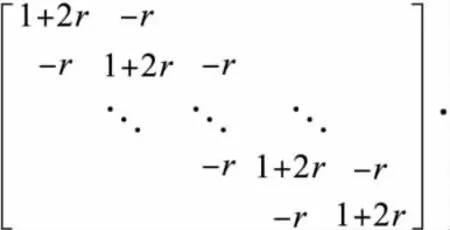
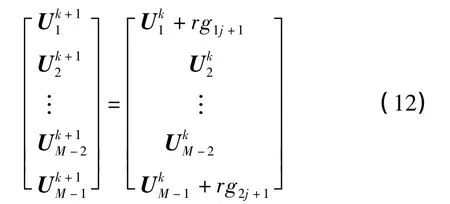
此方程组是三对角方程组，且系数矩阵严格对角占优，故解存在唯一.通过在每一时间层上求解一个这样的线性方程组得到在各个时刻各个网格点上的函数值.

Crank-Nicolson格式:将(8)式与离散化的初边值条件联立并整理，得差分方程组:

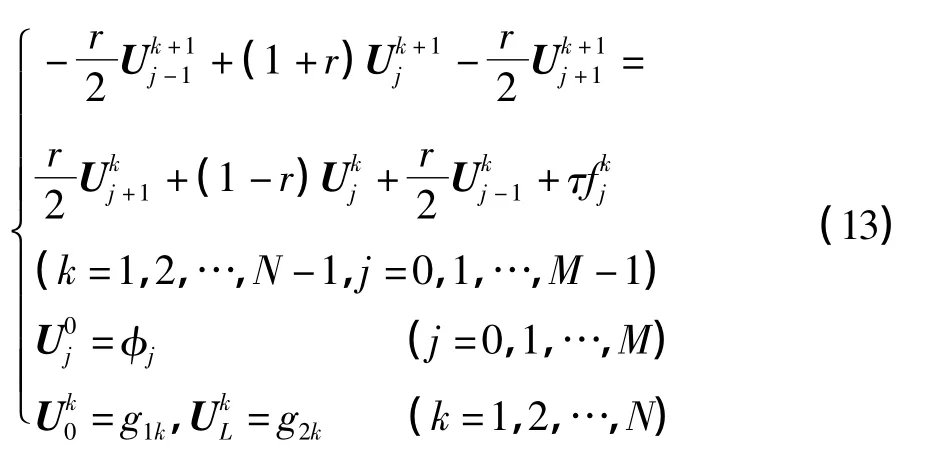
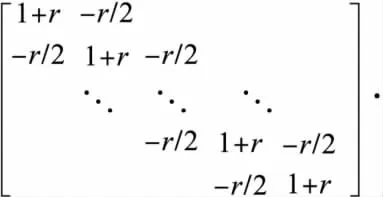
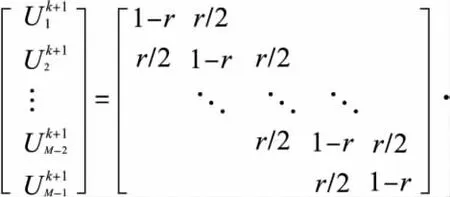
此方程组的系数矩阵严格对角占优，差分方程组解存在唯一.

程序如下:

Du Fort Frankel格式:将(7)式与初始条件及第一类边界条件式联立并整理将格式改写为:

由于此格式是3层格式，需要事先知道前面2个时间层上的解，第1层上的解通过对初始条件离散可得，第2层上的解使用前面的任意1种2层差分格式得到，再用此格式求解其余时间层上的解.程序核心代码如下:

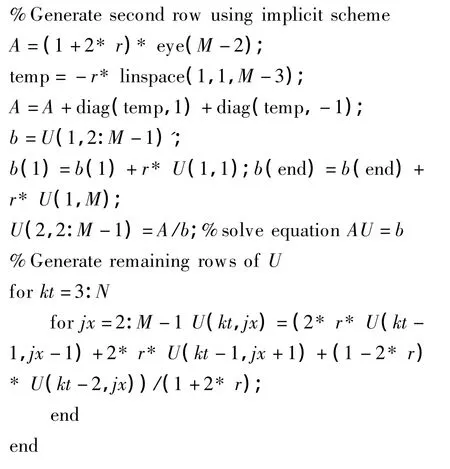
3 数值实验

使用前面4种不同差分格式求解下面热传导方程的初边值问题.

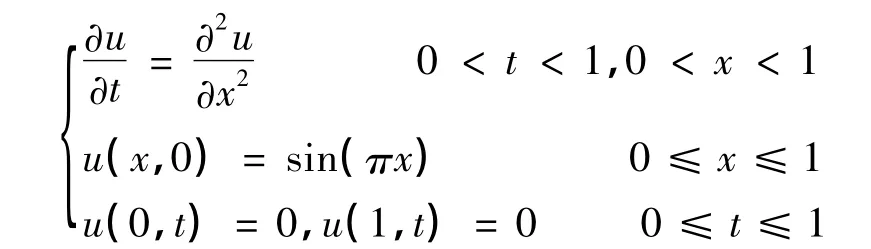
此问题的真解为u(x，t)=e－π2tsin(πx).

定义误差e=u－U，

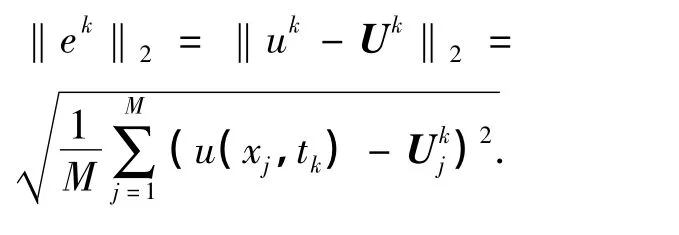
取空间步长h=0.1，求解结果如图1～图6所示.

图1 r=1时各种差分方法的误差‖ek‖2Fig.1 r=1 errors of several difference schemes‖ek‖2

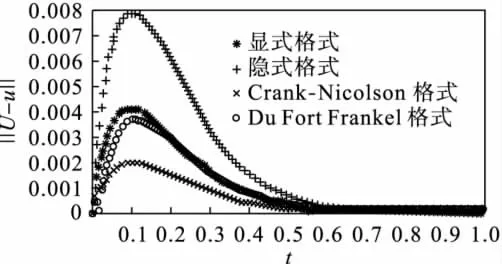
图2 r=时各种差分方法的误差‖ek‖2Fig.2 r=errors of several difference schemes‖ek‖2

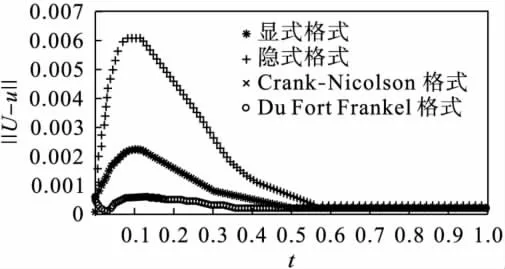
图3 r=时各种差分方法的误差‖ek‖2Fig.3 r=errors of several difference schemes‖ek‖2

图4 r=时各种差分方法的误差‖ek‖2Fig.4 r=errors of several difference schemes‖ek‖2

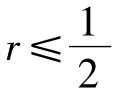
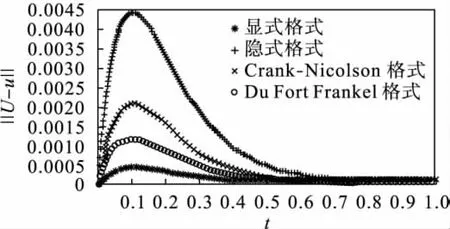
图5 r=时各种差分方法的误差‖ek‖2Fig.5 r=errors of several difference schemes‖ek‖2

图6 r=0.67时各种差分方法的误差‖ek‖2Fig.6 r=0.67 errors of several difference schemes‖ek‖2

4 结论

给出了使用MATLAB求解热传导方程几种差分格式的方法和部分主要程序，通过数值实验看到Du Fort Frankel格式和 Crank-Nicolson格式是误差较小且实用的方法.

［1］ 胡健伟，汤怀民.微分方程数值方法［M］.2版.北京:科学出版社，2007:131－138.

［2］ Morton K W，Mayers D F.Numerical Solution of Partial Differential Equations［M］.2thed.Cambridge UK:Cambridge University Press，2005:19－26.

［3］ 郑阿奇.MATLAB实用教程［M］.北京:电子工业出版社，2005:175－182.

［4］ 单毅.常微分方程的MATLAB解法［J］.武汉大学学报(工学版)，2003，36(z2):150－152.

［5］ 何双.MATLAB在常微分方程初值问题的应用［J］.长春师范学院学报(自然科学版)，2005，24 (3):17－19.［6］ 唐洪浪，桂现才.用MATLAB符号工具箱编程求常微分方程的通解［J］.洛阳师范学院学报，2005，24(2):81－84.

［7］ 王飞，裴永祥.有限差分方法的MATLAB编程［J］.新疆师范大学学报(自然科学版)，2003，22 (4):22－27.

［8］ 高理平，杨光.两点边值问题有限元方法的程序实现与计算分析［J］.山东师范大学学报(自然科学版)，2009，24(1):1－5.

［9］ 李灿，高彦栋，黄素逸.热传导问题的matlab数值计算［J］.华中科技大学学报(自然科学版)，2002，30(9):91－93.