基于Keren配准和插值的快速超分辨率图像重建*

李展 韩国强 陈湘骥 廖秀秀

(1.华南理工大学计算机科学与工程学院，广东广州510006;2.华南农业大学信息学院，广东广州510642)

数字图像处理技术在各个领域的广泛应用使人们对图像和视频的质量提出了更高的要求.超分辨率图像重建是指由一幅或多幅低分辨率(LR)的观测图像或视频重建高分辨率(HR)图像或视频的过程［1］.由于超分辨率技术是用后期图像和视频处理的手段对已有图像进行软件上的加工以增强图像视频的质量，比起改变硬件设备的方式更为灵活，成本也更低，自1984年Tsai等［2］提出该术语以来，超分辨率重建已经成为数字图像处理领域的研究热点之一.

超分辨率图像重建经典算法有Tsai等［2］的基于频域的算法、Stark等［3］的凸集映射法 (POCS)、Kim 等［4］的非均匀插值法(NI)、Irani等［5］的迭代后向映射法(IBP)、Schultz等［6］的最大后验概率法(MAP)等.Zomet等［7］改进了迭代后向映射法，增强了它对噪声、模糊不确定和运动误差的鲁棒性(RIBP).Elad等［8］提出了一个结合了最大后验概率和凸集映射算法的超分辨率重建框架，以此定义一个新的凸优化问题.Pham等［9］提出了一种结构适应的归一化卷积法 (SANC)，采用两遍归一化卷积实现超分辨率重建.Datsenko等［10］结合数据库和人工智能中的一些算法给出了基于学习的超分辨率重建.Anbarjafari等［11］利用小波变换分解低分辨率图像序列进行超分辨率重建.Pestak［12］在假设全局运动估计参数已知的情况下，提出了一种基于插值的超分辨率重建方法，该算法没有考虑配准算法的误差，且其中的门限尺寸阈值对不同的图像需取不同值，过小或过大会造成空洞或模糊.韩玉兵等［13］提出了一种基于加权最小二乘滤波的帧间数据融合算法，在单帧图像插值反卷积和运动补偿权值矩阵的基础上实现了视频序列超分辨率重建框架.周波等［14］首先对低分辨率图像利用Robert算子进行边缘检测，提出了一种基于改进的Keren配准和SANC的超分辨率重建算法，但没有提及关于算法执行速度的问题.

本研究实现了一种基于Keren配准和模板卷积的快速超分辨率算法，用于对静态场景图像序列的超分辨率重建.

1 图像退化模型和运动模型

1.1 退化模型

在超分辨率问题中，为了从一系列的低分辨率图像中重建出一幅高分辨率的图像，往往假设这些低分辨率图像序列是由高分辨率图像经过运动、模糊、下采样、加噪这些降质过程得到的，如式(1)所示［2］:

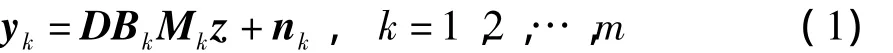
式中:yk是m幅分辨率为N1×N2图像中的第k幅;z是需要重建的qN1×qN2大小的图像;q是放大因子;D、Bk、Mk和 nk分别代表下采样矩阵、模糊矩阵、运动补偿矩阵和加性噪声向量.这个模型描述了图像降质退化的过程.如果不考虑模糊和噪声的因素，式(1)可以简化为［6］:

式中:Ak是配准矩阵，相当于下采样和运动补偿矩阵的乘积;z'是一幅具有模糊和噪声的高分辨率图像.本研究先通过图像配准算法估计平移和旋转参数从而得到yk和z'之间映射关系的Ak矩阵，然后采用插值和填充的方法计算z'中的像素值，最后采用常规的去模糊去噪方法做后期处理，获得最终的重建图像.重建过程如图1所示.

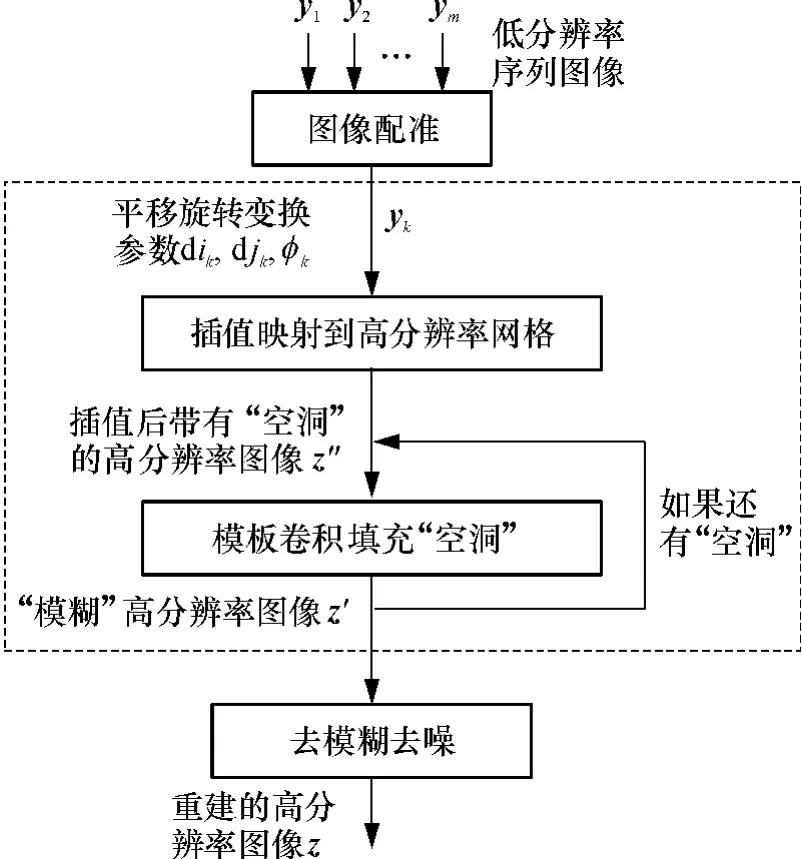
图1 基于插值和模板卷积的快速超分辨率图像重建流程图Fig.1 Flowchart of fast super-resolution image reconstruction based on interpolation and template convolution

1.2 运动模型

如果假定图像序列是对静态场景在短时段内的多次拍摄，并且拍摄时相机只有微小的移动，此时可以使用全局的平面平移或旋转模型来描述图像之间的运动关系［15］:

式中:(z't，z's)是模糊高分辨率图像z'中像素点的坐标，有 z't=1，2，…，qN1，z's=1，2，…，qN2;(yki，ykj)是第k幅低分辨率图像yk中像素点的坐标，有yki=1，2，…，N1，ykj=1，2，…，N2;(dik，djk)是平移量;φk是旋转角.此时，配准过程就是估计dik、djk、φk3个参数的值.

2 基于插值的鲁棒超分辨率算法

在众多超分辨率重建算法中，基于插值的方法具有简单、快速、适合于实时计算等特点.基于插值的多帧超分辨率技术通常将超分辨率重建的过程分为图像配准、插值重建和图像恢复3个步骤［16］.图像配准是对齐低分辨率图像序列，估计图像帧间的运动关系，获得描述低分辨率图像间变换关系的参数或矢量场;插值是在配准的基础上将多幅低分辨率图像中的信息采用插值的方式融合到高分辨率的网格，重建一幅高分辨率图像;最后的图像恢复一般指去模糊去噪等.本研究重点关注第2个步骤，基于插值的超分辨率重建.

2.1 文中提出的算法的原理

对原始连续场景采样后的高分辨率数字图像z'是本研究重建的目标，假设低分辨率图像是由这幅高分辨率图像经下采样后得到的，如图2所示.根据退化模型式(2)，重建的高分辨率图像z'跟实际低分辨率图像yk之间存在映射关系Ak.可以认为，低分辨率图像中像素点的灰度值是高分辨率图像中相应像素点灰度值信息的体现.同一个高分辨率图像的像素点在低分辨率图像序列里存在的对应点的帧数越多，说明该点出现的次数越多，则反映该点灰度值的信息越多，计算得到的该点灰度值“可信度”越大.反之，高分辨率图像中也存在在低分辨率图像序列中找不到对应点的像素，也就是文中所指的“空洞”，此时空洞处的灰度值因为没有对应点而无法确定.利用“可信”的像素来计算“不确定”的空洞值是本算法的基本思想和特点.

图2 快速鲁棒超分辨率图像重建算法原理Fig.2 Principle of fast and robust super-resolution image reconstruction algorithm

2.2 配准算法

插值类超分辨率算法的局限性在于重建效果很大程度上依赖于图像配准算法的准确程度.一方面，为获得更高分辨率的重建效果，配准算法应能够估计低分辨率图像帧间亚像素级的运动位移参数［1］;另一方面考虑到实时应用的要求，配准算法应具有计算负载低、执行快速有效的特点.Vandewalle［17］研究比较了 Keren、Marcel、Lucchese 等［18-20］和 Vandewalle等［15，17，21］提出的 4 种用于估计全局平移和旋转参数的配准算法.其中Keren算法是利用一阶Taylor展开的空域配准算法，其余3种是基于傅里叶变换的频域配准算法.Vandewalle［17］的研究发现，Keren 算法和Vandewalle算法的精度明显比另外两种算法高;Keren算法对平移量的估计与Vandewalle算法的配准精度相当，对旋转量的估计精度优于Vandewalle算法.而且Keren算法简单快速，执行效率高，是超分辨率重建中广泛使用的一种亚像素级配准方法.本研究提出的超分辨率重建方法对一定精度范围内的配准参数误差不敏感，具有较强的鲁棒性，因此权衡精度和速度，本研究选择Keren算法实现对低分辨率图像序列的配准，以适应实时应用的需要.

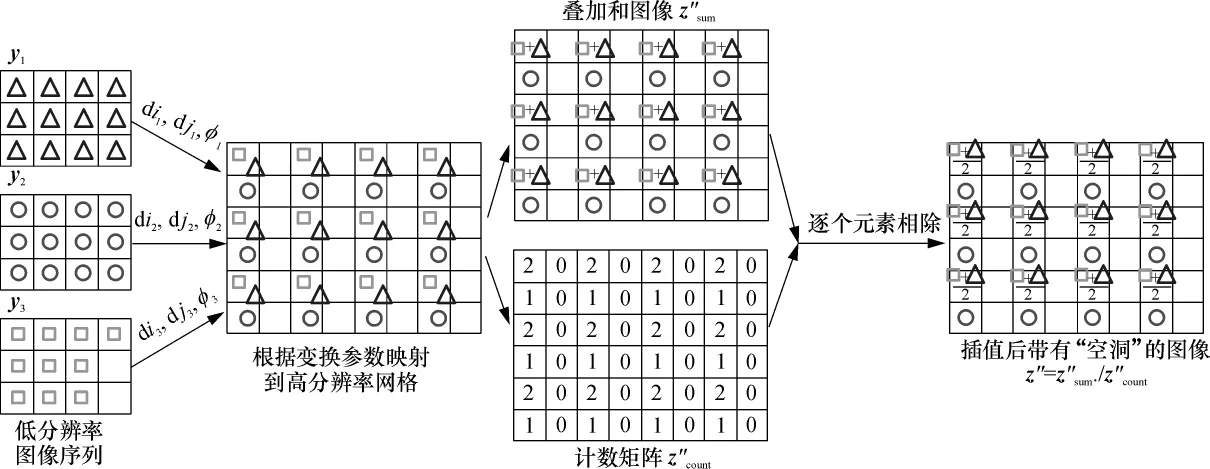
图3 低分辨率图像向高分辨率网格的映射和插值过程Fig.3 Map and interpolation process from low-resolution images to high-resolution grid

2.3 插值映射

有了配准参数后，为了实现低分辨率图像向高分辨率网格的映射，采用了图3所示的流程.图3中z″sum./z″count表示两个矩阵z″sum与z″count中对应元素逐点相除.首先，利用变换参数将所有低分辨率图像中的像素点坐标换算成高分辨率网格的坐标，并对这些计算得到的坐标值取整，得到一张非均匀采样的高分辨率图像.再将所有落入同一个像素区域的所有点的灰度值求算术均值，作为此网格点上的像素值.实现时，定义了两个跟高分辨率图像同样大小的叠加图矩阵和计数矩阵，分别计算落入一个像素区域的点灰度值和和点个数.具体步骤如下:

(1)取低分辨率图像yk，对每个像素点(yki，ykj)用式(3)计算它在高分辨率网格中的坐标值(z″t，z″s);

(2)对(z″t，z″s)计算值取整，若 (z″t，z″s)的值在合理坐标范围内，即 1≤z″t≤qN1且 1≤z″s≤qN2，则在叠加图z″sum中对应像素点上加入点(yki，ykj)的像素灰度值，同时计数矩阵z″count对应位置计数值加1;

(3)若还有低分辨率图像帧未被处理，转步骤(1)继续，否则，转步骤(4)

(4)将叠加图所有非“空洞”数值与计数矩阵对应位置点数据相除，得到插值后带有“空洞”的高分辨率图像 z″.

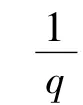
2.4 基于模板卷积的填充算法

低分辨率图像之间配准时，存在由于运动或遮蔽引起的“移进移出”现象.有些低分辨率图像中可见的像素由于“移出”而在高分辨率图像中消失，因此并非低分辨率图像中提供的所有信息都能用于高分辨率图像的重建.另一方面，高分辨率图像中有些像素点可能在所有的m幅低分辨率图像中都找不到对应点，因此映射完成之后可能在高分辨率网格中还留有一些尚未赋值的“空洞”像素.一般地说，放大因子q一定时，用于重建的低分辨率图像帧数m越多，所能提供的信息也就越多，“空洞”数就越少.如何填补这些“空洞”像素也是提高质量的重要环节.

采用迭代模板卷积算法来填充“空洞”像素，如图4所示.图4中空白方块表示“空洞”，灰色表示填充，不同深度的灰色表示在不同次数的卷积中依次填充.用一个3×3的卷积模板在有“空洞”的高分辨率图像z″上滑动，其中参数w由实验测定，实验表明，对大多数图像，w的最佳取值在4.5～7.3之间，本研究中取w=6.遇到“空洞”像素时将模板中的权值与“空洞”3×3邻域中对应像素值的乘积相加，然后除以实际参加相加的权值并进行归一化.具体如下:

1)取带有“空洞”的高分辨率图像z″:对每个需要填充的“空洞”像素点(z″t，z″s)，用式(4)计算其灰度值:

式中:g(u，v)代表像素点(u，v)处的灰度值.有3类特殊情况:

(1)若需要填充的“空洞”像素位于图像边界，如图4中的A像素，则实际参加计算的邻域像素仅为在图像上的邻域点:

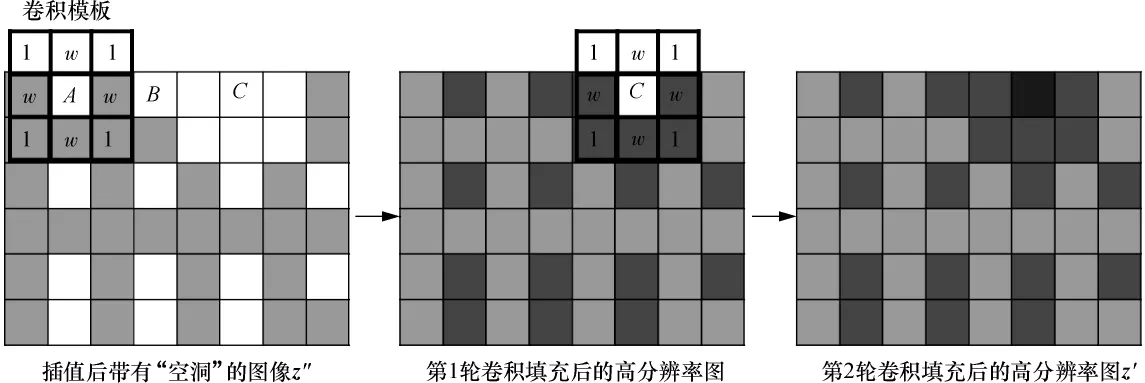
图4 迭代的模板卷积算法填充“空洞”像素的流程Fig.4 Holes filling procedure by iterative template convolution algorithm

(2)若“空洞”邻域也存在“空洞”，如图4中的B像素，则实际参加计算的邻域像素只计非“空洞”像素:

(3)若“空洞”邻域全是“空洞”，如图4中的C像素，则暂不填充该像素，留到下一轮卷积处理.

2)若z″中还有未填充的“空洞”，转步骤1)继续，否则，转步骤(3).

3)输出完全填补所有“空洞”的高分辨率图像 z″.

一般而言，图像中“空洞”比例在30%以内时，经过第1轮模板卷积之后，大部分的“空洞”像素(图像上邻域内有非“空洞”像素的那些“空洞”像素)已经被填充.空洞较多的图像一般进行2到3轮卷积也可以全部填满.“空洞”比例过高，意味着低分辨率图像帧数m相对于放大因子q太小，或者低分辨率图像中可用于重建的信息量不够，此时卷积迭代次数较多，重建效果较差.

3 实验结果及分析

本研究在matlab7.0环境中实现和测试了文中提出的算法，并通过实验将提出的算法与NI、POCS、RIBP 和 SANC 进行了对比［3-4，7，9］.参与对比的算法都先采用Keren算法进行低分辨率图像帧间的配准，再进行超分辨率重建.其中非均匀插值法使用matlab中基于三角形的三次插值的griddata函数实现;另外几种算法由Vandewalle［17］提供的开放源码软件superresolution 2.0实现.所有算法均在 Intel Pentium 2.80GHz双核处理器和1.0GB内存的普通PC机上运行测试.重建图像质量以峰值信噪比(PSNR)和均方误差(MSE)作为客观评价标准，执行时间比较以秒为单位.

第1组实验对由一幅100×100的高分辨率手机键盘图像(见图5(a))平移和下采样产生的4幅50×50的低分辨率图像进行超分辨率重建(q=2).4幅低分辨率图像的实际位移量和由Keren算法计算得到的位移量见表1，第1幅图像y1是参考帧(见图5(b)).重建的结果见图5，每个子图的右上角是局部放大图.从视觉上看，除了RIBP算法(见图5(e))明显有振铃效应外，其余算法的重建效果差别不大，但超分辨率重建后的清晰度都显著优于单幅低分辨率图像(见图5(b)).

图5 手机键盘图像序列超分辨率重建结果Fig.5 Super-resolution reconstruction results of cellphone keyboard image sequences

表1 手机键盘低分辨率图像帧间的平移量Table 1 Shifts of low-resolution cellphone keyboard images

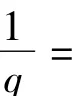
第2组实验对象为一幅高分辨率的国际标准化组织(ISO)标准分辨率测试图的512×512的局部图(见图6(a)).先对该图进行旋转、平移和下采样(q=4)，得到9幅128×128的低分辨率图像.实验结果见图6，每个子图的左上角是局部放大图.为了显示多帧超分辨率重建的效果，将低分辨率参考帧y1(见图6(b))进行双三次插值的结果也列入算法的比较中.从图6中可见，由于采样不足，低分辨率图像y1中出现了明显的混叠条纹伪影(见图6(b)局部图)，而单帧双三次插值并不能有效去除这些伪影(见图6(c)).表3给出了第2组实验中各算法的量化比较，其中POCS算法和RIBP算法因失效没有列入.从图6和表3可看出，有效的3种(见图6(f)、(g)、(h))多帧超分辨率重建算法在重建效果上都优于单帧图像双三次插值，其中文中提出的算法和SANC算法的峰值信噪比大致相当，略优于NI，但文中提出的算法与NI、SANC相比在执行时间上具有明显优势.比较表3中Keren配准和直接输入参数的执行时间还可看出，文中提出的算法时耗主要是Keren配准算法(2.6463s－0.6214s≈2.02s)，若能够改进配准算法的时耗，可使算法进一步加速.

表2 手机键盘图像序列超分辨率算法的量化比较Table 2 Quantitative comparison of SR algorithms for cellphone keyboard image sequences

图6 ISO分辨率测试图像序列超分辨率重建结果Fig.6 Super-resolution reconstruction results of ISO resolution chart image sequences

表3 ISO分辨率测试图像序列超分辨率算法的量化比较Table 3 Quantitative comparison of super-resolution algorithms for ISO resolution chart image sequences

4 结语

本研究在用Keren算法进行低分辨率图像序列配准的基础上，提出和实现了一种利用插值映射和模板卷积填充的快速超分辨率重建方法.实验表明，文中提出的算法对平移参数的配准误差具有一定的鲁棒性，重建效果较好，在执行速度上具有较大优势，提供了超分辨率算法实时应用的可能性.下一步研究将改进配准算法的执行效率，使文中提出的算法进一步优化.

［1］ Park S C，Park M K，Kang M G.Super-resolution image reconstruction:a technical overview ［J］.IEEE Signal Processing Magazine，2003，20(3):21-36.

［2］ Tsai R Y，Huang T S.Multiframe image restoration and registration ［J］.Advances in Computer Vision and Image Processing，1984，1(2):317-339.

［3］ Stark H，Oskoui P.High resolution image recovery from image-plane arrays，using convex projections［J］.Journal of the Optical Society of American，1989，6(11):1715-1726.

［4］ Kim S，Bose N K，Valenzuela H.Recursive reconstruction of high resolution image from noisy undersampled multiframes［J］.IEEE Transactions on Acoustics，Speech，and Signal Process，1990，38(6):1013-1027.

［5］ Irani M，Peleg S.Improving resolution by image registration ［J］.Computer Vision，Graphics and Image Processing，1991，53(3):231-239.

［6］ Schultz R R，Stevenson R L.Extraction of high-resolution frames from video sequences［J］.IEEE Transactions on Image Processing，1996，5(6):996-1011.

［7］ Zomet A，Rav-Acha A，Peleg S.Robust super-resolution［C］∥Proceedings of 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Hawaii:IEEE，2001:645-650.

［8］ Elad M，Feuer A.Restoration of a single superresolution image from several blurred，noisy，and undersampled measured images［J］.IEEE Transactions on Image Processing，1997，6(12):1646-1658.

［9］ Pham T Q，van Vliet L J，Schutte K.Robust fusion of irregularly sampled data using adaptive normalized convolution［J］.EURASIP Journal on Applied Signal Processing，2006，2006(10):236-247.

［10］ Datsenko D，Elad M.Example-based single document image super-resolution:a global MAP approach with outlier rejection ［J］.Multidimensional System and Signal Processing，2007，18(2):103-121.

［11］ Anbarjafari G，Demirel H.Image super resolution based on interpolation of wavelet domain high frequency subbands and the spatial domain input image［J］.ETRI Journal，2010，32(3):390-394.

［12］ Pestak T C.Development of an efficient super-resolution image reconstruction algorithm for implementation on a hardware platform［D］.Dayton:Department of Electrical Engineering，Wright State University，2010.

［13］ 韩玉兵，束锋，吴乐南.基于加权最小二乘滤波的视频序列超分辨率重建［J］.电子与信息学报，2009，31(1):120-123.Han Yu-bing，Shu Feng，Wu Le-nan.Super-resolution reconstruction of video sequence based on WLS filtering［J］.Journal of Electronics ＆ Information Technology，2009，31(1):120-123.

［14］ 周波，江月松，唐华，等.基于改进Keren配准方法的超分辨率算法［J］.激光与光电子学进展，2010，47(5):051006-1-051006-6.Zhou Bo，Jiang Yue-song，Tang Hua，et al.A super-resolution algorithm based on modified approach of Keren registration method［J］.Laser＆ Optoelectronics Progress，2010，47(5):051006-1-051006-6.

［15］ Vandewalle P，Susstrunk S，Vetterli M.A frequency domain approach to registration of aliased images with application to super-resolution ［J］.EURASIP Journal on Applied Signal Processing:Special Issue on Super-Resolution，2006，2006:1-14.

［16］ Patanavijit V.Super-resolution reconstruction and its future research direction［J］.Assumption University Journal of Technology，2009，12(3):149-163.

［17］ Vandewalle P.Super-resolution from unregistered aliased images［D］.Lausanne:School of Computer and Communication Sciences，Ecole Polytechnique Federale de Lausanne，2006.

［18］ Keren D，Peleg S，Brada R.Image sequence enhancement using sub-pixel displacement［C］∥Proceedings of IEEE Conference on Computer Vision and Pattern Recognition.Ann Arbor:IEEE，1988:742-746.

［19］ Marcel B，Briot M，Murrieta R.Calcul de translation et rotation par la transformation de fourier［J］.Traitement du Signal，1997，14(2):135-149.

［20］ Lucchese L，Cortelazzo G M.A noise-robust frequency domain technique for estimating planar roto-translations［J］.IEEE Transactions on Signal Processing，2000，48(6):1769-1786.

［21］ Vandewalle P，Sbaiz L，Vandewalle J，et al.Super-resolution from unregistered and totally aliased signals using subspace methods［J］.IEEE Transactions on Signal Processing，2007，55(7):3687-3703.