基于实际波动率的我国股市波动率实证研究
吴有英,马玉林
(1.山东财政学院会计学院;2.山东财政学院科研处,山东济南 251000)
一、前言
股票收益的波动率,对于组合选择、风险管理以及期权定价都相当重要。我们引用克莱夫·格兰[1](2003)的一句话“过去十几年,特别是在时间序列方面,主要是波动率占据了研究的主要内容和重心”,由引可见,波动率在金融领域的地位非同一般。而对于波动率的研究,又主要集中在对它的度量和预测。回顾过去,度量波动率最初的方法始自于马克维茨的MPT理论,该理论的普及使得标准差方法极度盛行,从而使得它在经典金融学理论中得到了广泛的应用,如后来的CAPM模型、APT理论以及B-S模型等。在随后的研究中,经济学家们观察到股票收益的波动呈现出丛聚性(clustering)和时变性(time varying),收益率正态分布的假定受到了广泛的质疑。直到1982年,Engle[2]在研究英国通货膨胀率时提出了ARCH模型,它成功地模拟了波动率的丛聚性和时变性,从而获得了空前的成功,以至于21年后,Engle因ARCH模型获得了诺贝尔经济学奖。波动率的大规模研究应该始自于Bollerselve[3](1986), GARCH模型的提出一方面更好地解释了波动率的持续性,弥补了ARCH模型的不足,另一方面为后续模型的提出提供了一个良好的基础。毫无疑问,GARCH模型意义深远,以至于直到今天,GARCH(1,1)模型仍是GARCH类模型中应用最为广泛的一个。在随后的发展中,又有许多新的方法出现,如Taylor(1986)提出了随机波动(Stochastic Volatility)模型,以及度量波动率的一些非参数方法,如收益绝对值、收益极差等。
众多波动率度量方法的盛行必然会带来一个问题,哪种度量方法度量得最精确?这就涉及到对各种波动率度量方法和度量效果的一个评价,但评价标准是什么,也即真实的波动率是什么?事实上,真实的波动率本身又是无法观察到的,这就使该问题的解决陷入一个尴尬的境地。
Merton[4](1980)指出:在样本频率充分大的条件下,通过加总高频平方变量的值,一个独立同分布随机变量的方差(在一个固定期限内),可以被估计得充分精确。Merton(1980)、French,Schwert,Stambaugh[5](1987)等用日收益数据来估计股票月波动率,实际波动率(Realized Volatility)被正式提出。经过十多年的发展,实际波动率理论也渐趋完善。它的出现,使得真实波动率成为可观测的变量,从而使得上述问题的解决有了方向。它完全地打破了传统的波动率研究思路,彻底地颠覆了传统的波动率度量方法,成为引领波动率研究的一个崭新的亮点和新的方向。
在众多的研究中,最具代表性的当属Andersen等人的一系列研究,如Andersen,Bollerslev[6](1998),Andersen,Bollerslev,Diebold,Labys[7-10](1999,2000,2001,2003,后简称ABDL),Andersen,Bollerslev,Diebold,Ebens[11](2001,后简称ABDE),Andersen,Bollerslev,Diebold[12](2002)。其它的研究如:Schwert(1998),Ebens[13](2000),Oomen[14](2001),Bandi[15](2003)等等。
实际波动率在国内还属于新兴事物,对它的认识才刚刚开始,对它的研究可谓凤毛麟角。黄后川[16](2003)利用A、B股指数对实际波动率进行了较为系统的研究。施红俊等[17](2003)对实际波动率理论和实证进行过一个综述。
本文的目的在于揭开实际波动率的面纱,对上述实际波动率及其相关变量的性质进行实证研究,让人们对它有一个更加清晰的认识,从而可以利用它为投资服务。
二、理论背景、算法及已有结论
实际波动率的理论背景主要是基于收益分解和二次变动理论。
假定N×1对数价格向量Pt,遵循如下多变量连续时间随机波动扩散模型:

Wt表示N维布朗运动过程,Ωt为N×N维正定扩散矩阵,且严格平稳。条件于样本路径特征μt和Ωt下,在[t,t+h]上连续复合收益为:

它服从Gaussian分布:

借助于二次变动理论,可以得知,在△→0时,有:
则实际协方差矩阵可以表示为:
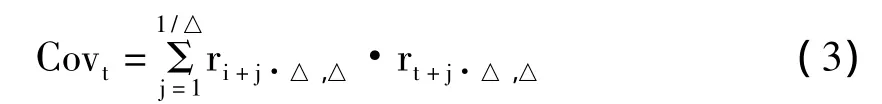
对于第j只股票,其实际方差可用矩阵对角线上的元素表示为:={Covt}j,j
对数标准差表示为:lvj,t=log(Vj,t);我们把第i只股票和第j只股票的相关系数表示为:Corri,j,t={Covt}i,j/Vi,t·Vj,t
国外的文献在大量实证研究的基础上,得出的一些基本的结论有:
①ri,t/Vi,t的分布接近于正态;即:日收益序列经日实际波动率标准化后的序列近于正态分布。
③Covi,j,t显著右偏,但Corri,j,t却接近于正态分布;即:第i只股票与第j只股票的实际协方差所构成的序列的分布显著右偏,但它们之间的实际相关系数所构成的序列的分布却近于正态。
④lVj,t和Corri,j,t具有长记忆性;即:对数实际波动率序列和实际相关系数序列具有长记忆性特征。
⑤LogVi,t和logVj,t具有显著的相关性。即:任两只股票的对数波动率之间具有显著的相关性。
三、实证及分析
(一)样本说明
由于实际波动率要求样本有尽可能好的流动性,故本文以上证180样本股为总样本,根据实证的需要,从中随机抽取30只,股票代码及名称见表1。实际波动率要求样本有尽可能高的频率,本文采用日内分钟交易数据,时间跨度为2008年1月7日至2009年12月31日。数据来源于润金数据库。以下实证结果在SAS8.2上实现。
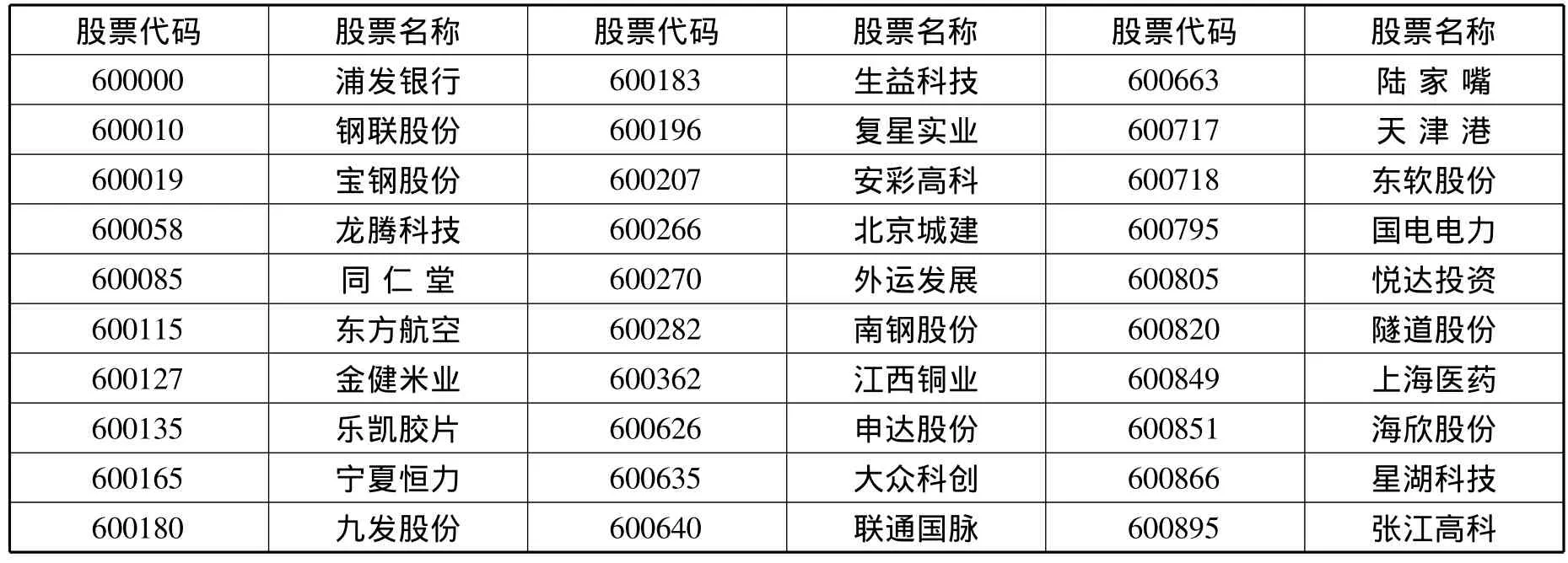
表1 样本股基本信息
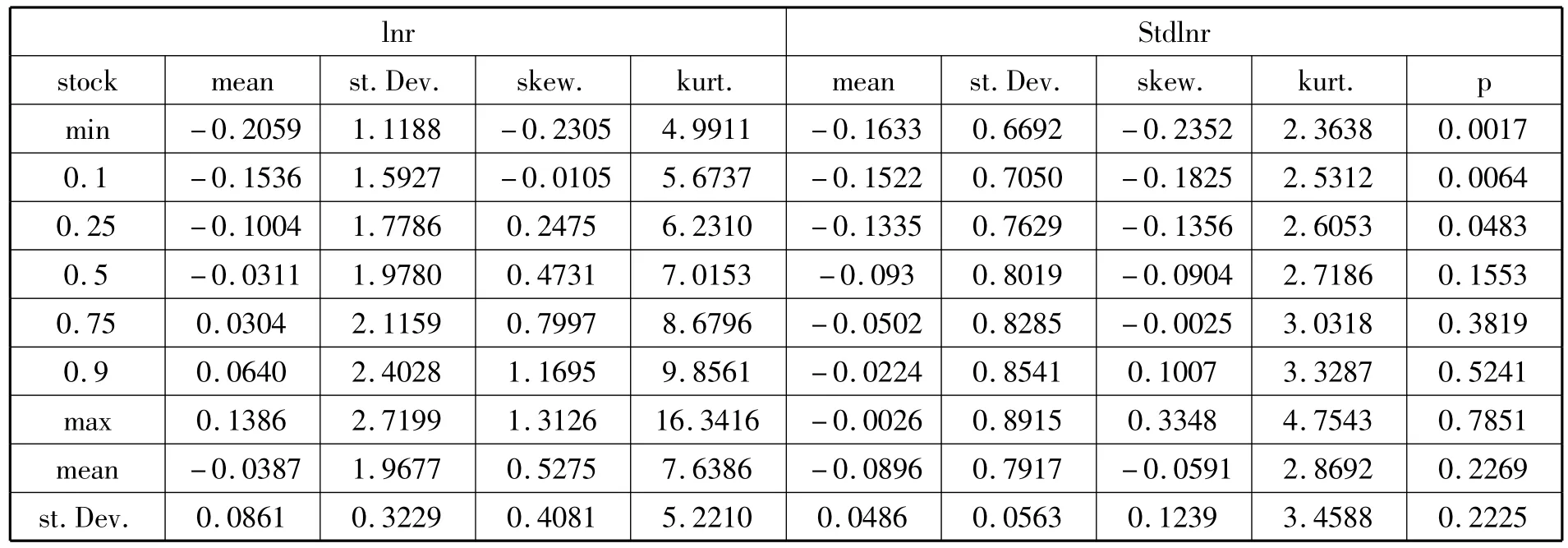
表2 收益率和标准化收益序列的描述性统计值(30只样本)
(二)实证结果及分析
1.收益和标准化收益
表2展示了30只样本的收益率序列及标准化收益序列分布的描述性统计特征。
从表2可以看出,收益序列表现出明显的尖峰状态,30个样本中最小的峰度值为4.99,平均峰度值为7.64;并且表现出明显的右偏趋势,偏度的中位数为0.47,均值为0.53。而对于标准化收益序列,其峰度和偏度的分布则完全不同。其峰度值分布在3左右,30个样本中最小的峰度值为2.36,最大的为4.75,中位数为2.72,较之收益序列的峰度下降了很多;它的偏度的均值为 -0.059,比较接近于0。从最右列的正态性检验的P值可以看出,30只样本中有75%以上的样本在1%显著水平下不拒绝正态分布(在5%水平下,有22个不拒绝正态分布,在1%水平下,有26个不拒绝),这与GARCH模型中的标准化残差的尖峰分布形成了鲜明的对比,Bollerslev,Engle,Nelson(1994)对此进行了一般的讨论。图 1为600085(从30只样本中随机抽取)的标准化收益序列的核密度图。

图1 标准化收益序列的核密度图
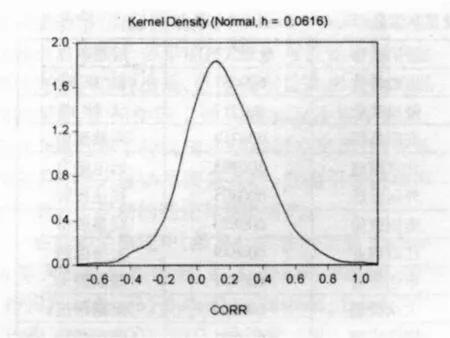
图2 实际相关系数序列的核密度图
2.方差和对数实际波动率
下面给出了实际方差、实际波动率及对数实际波动率分布的描述性统计量。
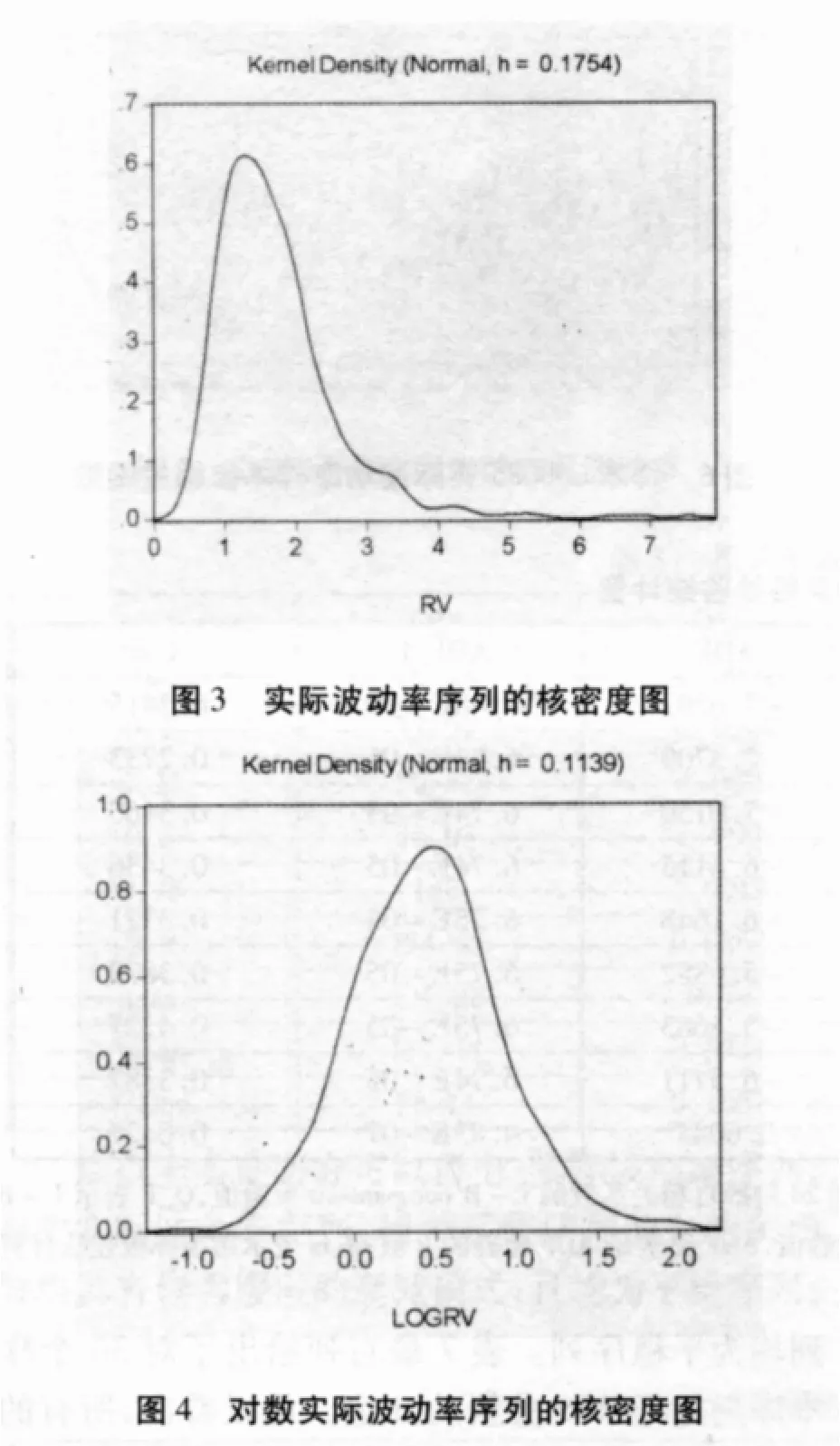
可以看出,实际方差的分布呈显著的右偏,实际波动率的右偏趋势有所减弱,偏度的中位数从7.24减到了2.69,说明实际波动率有接近于对称分布的趋势;再看对数实际波动率的偏度,虽然还是呈右偏的趋势,但其程度却大大减小,其偏度的中位数为0.52。峰度的变化趋势则更为明显,从实际方差到对数实际波动率,峰度的中位数从73.95减到了3.67。对30个样本的对数实际波动率序列进行正态性检验,在5%水平下,有7只不拒绝正态分布,在1%水平下,有9只不拒绝。由此可以发现,虽然不能说对数实际波动率呈现出了正态分布,但它确实在向正态分布靠近。图3、图4为样本600085实际波动率及对数实际波动率的核密度图。
上面的实证结果与ABDE(2001)的实证结论是一致的。关于对数实际波动率的分布近于正态的结论可以在 Taylor(1986),French,Schwert,Stambaugh(1987)的研究中找到原形,他们用日收益数来计算月实际波动率,发现月实际波动率的对数呈现出近于正态的分布。
以上的研究是基于单变量的收益和波动率的研究,然而在资产定价、组合选择以及风险管理中无一不涉及到多变量的情形。因此下面进一步研究变量之间的实际协方差和相关系数的分布特征。

表3 实际方差和实际波动率分布的描述性统计统计量
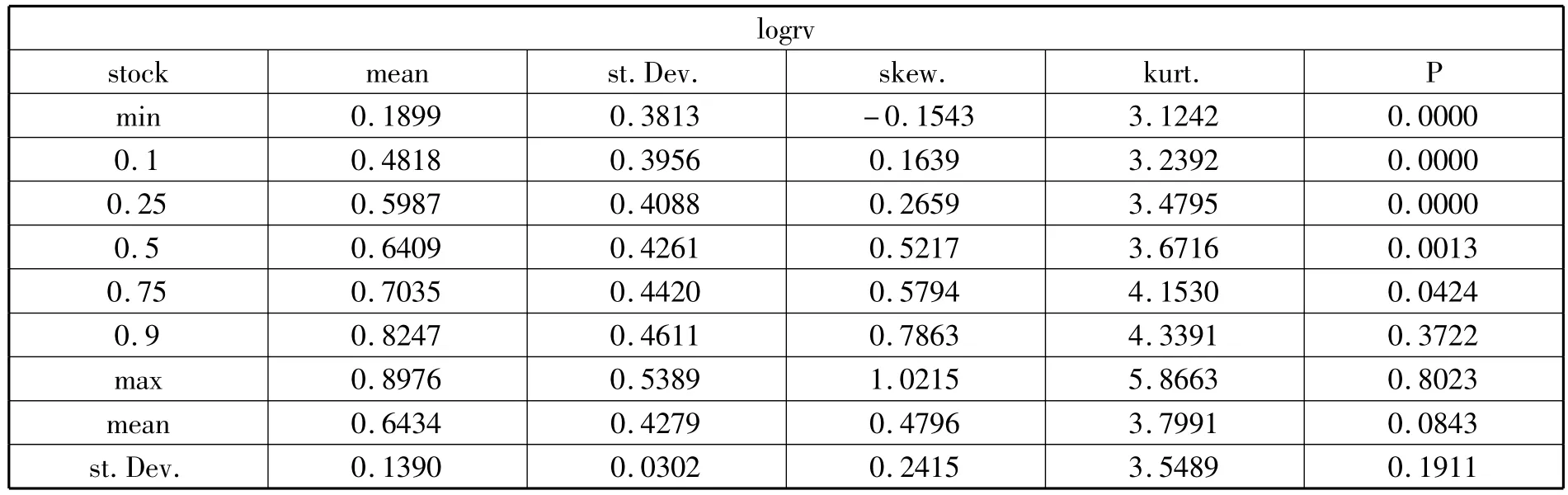
表4 对数实际波动率分布的描述性统计量
3.协方差和相关系数
实际协方差是计算30个样本中每一个样本序列与其它29个样本序列的实际协方差,计算的样本频率为5分钟,共得435个序列。由于30个样本不可能在所取的时间段上均有交易,因此,在计算的过程中笔者剔除了那些非共有的交易时段。
由表5可以看出,实际协方差呈显著的右偏尖峰状态,相关系数则呈轻微的右偏趋势。其偏度的中位数为0.019,峰度的中位数为3.15。对它进行正态性检验,在5%显著水平下,有382个序列不拒绝正态分布,在1%水平下,有416个不拒绝。表明相关系数序列比较接近于正态分布。图2为样本600085与样本600000的实际相关系数的核密度图。
4.相关性研究
下面对实际波动率、对数实际波动率及相关系数的相关性进行研究。为了更深入地研究实际波动率序列的相关性特点,首先对序列进行L-B Portmanteau检验,表6为30个样本进行各项检验后的百分位数值,从第三栏可以看出,其直到24阶的自相关函数值均高度显著,表明序列存在显著的自相关现象。仍以600085为例,图5为它的实际波动率序列图,从图中可以看出,波动率呈现出明显的丛聚性和相关性,这与ARCH类模型所刻画的波动率现象是一致的。但其自相关函数衰减较快(图6,至10阶左右后变得不显著);接着对序列进行单位根检验,表6的第五栏反应了ADF检验相应的P值,可以看出检验结果均高度显著,均拒绝单位根假定,说明序列均为平稳序列。最后对它们进行R/S分析,表6最末一栏为样本各序列R/S分析的结果,d的中位数为0.34,表明了原序列均存在显著的长记忆特征。
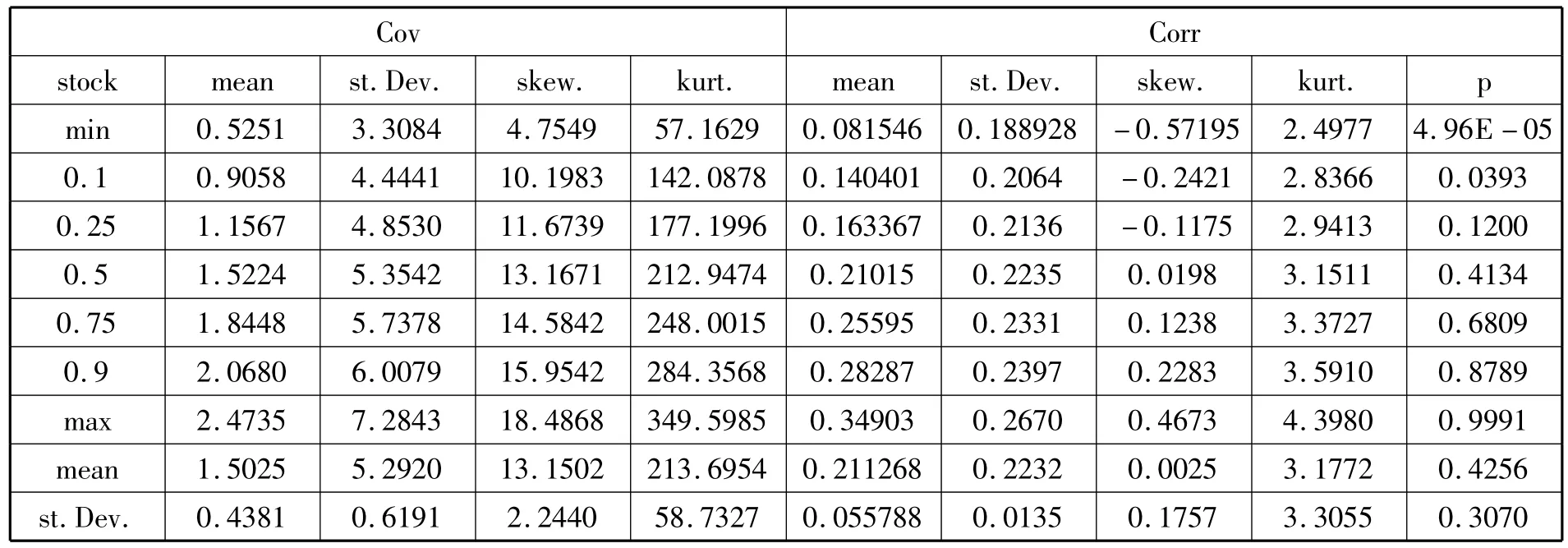
表5 协方差和相关系数的描述性统计特征
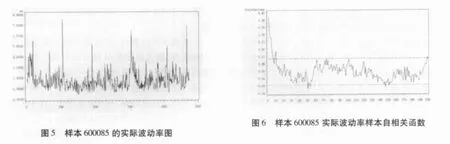
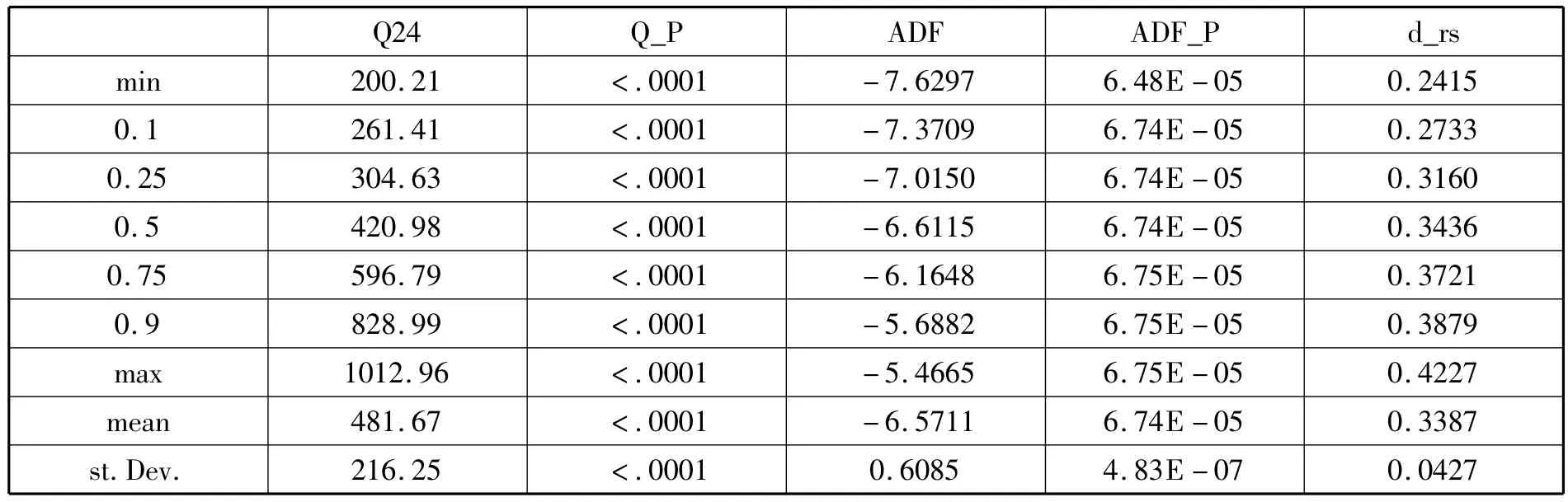
表6 实际波动率相关性检验统计量
表7为对数实际波动率各项检验的百分位数值,从中可以看出,所有样本自相关函数的24阶Q统计量均高度显著。对样本进行ADF检验,其检验值也高度显著,表明对数实际波动率样本序列均为平稳序列。表7最右列给出了对30个样本序列进行R/S分析的d值。可以看出,所有的样本均具有显著的长记忆特征。
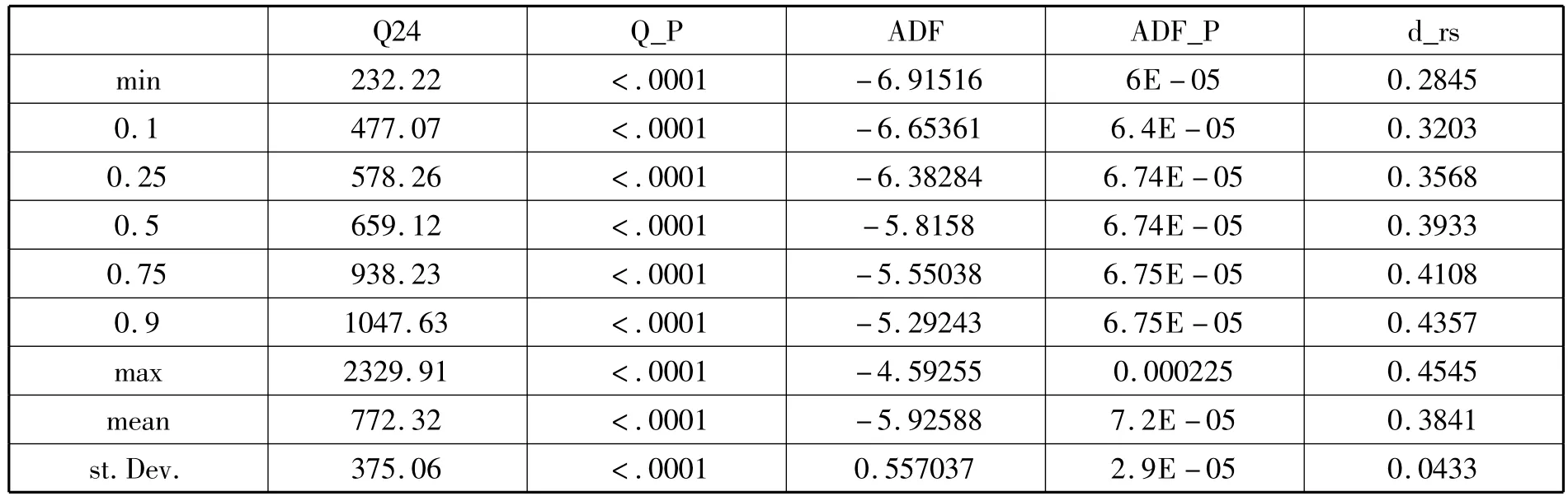
表7 对数实际波动率相关性检验统计量
样本600085的对数实际波动率值见图7,它同样表现出了波动率的丛聚性和相关性。它的样本自相关图见图8。虽然它并没有表现出缓慢的双曲衰减模式,但直至10阶左右时,它进入95%置信区间内。
表8概括了30个样本的435个相关系数序列的自相关检验值、单位根检验值以及长记忆检验值。从中可以看出,90%以上的相关系数的Q统计量高度显著,ADF检验值全部显著,R/S分析的结果也表明相关系数具有显著的长记忆特征。


表8 相关系数相关性检验统计量
从以上实证研究可以得出:实际波动率序列、对数实际波动率序列、相关系数序列的自相关函数均具有较为缓慢的衰减模式;且均为平稳序列;均具有显著的长记忆特征。下面对不同股票的对数实际波动率的相关性进行研究,表9为实证结果。

表9 对数实际波动率的相关系数的描述性统计特征
从上表可以看出,相关系数的中位数为0.43,表明各样本的波动率序列具有同向运动(comovement)的趋势,并且这种趋势较为强烈。ABDE(2001)也得出了类似的结论,并用波动率的因子结构作了解释。
四、结论
通过以上实证研究,本文可以得出以下结论:
1.经实际波动率标准化的收益率序列接近于正态分布;2.对数实际波动率序列的分布接近于正态;3.实际相关系数序列接近于正态分布;4.实际波动率序列、对数实际波动率及相关系数序列均具有显著的长记忆特征;5.不同股票的对数波动率序列之间具有显著的相关性。
可以发现,这与第二节提到的国外文献研究的结论是一致的。由此我们可以得出,实际波动率是一种理论,它并不局限于某个特定市场,我们研究它、认识它、了解它,从而可以利用它,为我们进行组合选择、风险管理服务。随着人们对实际波动率理论认识的深入,该理论的巨大应用价值一定会更加凸显。
[1]Poon,SH and Granger,Clive W.J.,2003,Forecasting Volatility in Financial Markets:A Review,Journal of Economic Literature.Vol.XLI,June 2003..478-539.
[2]Engle,Robert F.,1982,Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation,Econometrica,50,4,987-1007.
[3]Bollerslev,Tim,1986,Generalized Autoregressive Conditional Heteroskedasticity,Journal of Econometrics,31, 307-327.
[4]Merton,R.C.,1980,On Estimating the Expected Return on the Market:An Exploratory Investigation,Journal of Financial Economics,8,323-361.
[5]French,K.R.,G.W.Schwert and R.F.Stamb augh,1987,"Expected Stock Returns and Volatility,"Journal of Financial Economics,19,3-29.
[6]Andersen,T.G.&Bollerslev,T.,1998,Answering the skeptics:Yes,standard volatility models do provide accurate forecasts',International Economic Review 39,4,885 905.
[7]Andersen,T.G.,T.Bollerslev,F.X.Diebold and P.Labys,1999,realized volatility and correlation,www.ssc.upenn.edu/~fdiebold/papers/paper29/temp.pdf
[8]Andersen,T.G.,T.Bollerslev,F.X.Diebold and P.Labys,2000,Exchange Rate Returns Standardized by Realized Volatility are,Nearly Gaussian,Multinational Finance Journal,4,159-179.
[9]Andersen,T.G.,T.Bollerslev,F.X.Diebold and P.Labys,2001a,The Distribution of Realized Exchange Rate Volatility,Journal of the American Statistical Association,96,42-55.
[10]Andersen TG,Bollerslev T,Diebold FX,Labys P.2003.Modeling and forecasting realized volatility.Econometrica 71:579-625.
[11]Andersen,T.G.,T.Bollerslev,F.X.Diebold and H.Ebens,2001,The Distribution of Realized Stock Return Volatility,Journal of Financial Economics,61,43-76.
[12]Andersen TG,Bollerslev T,Diebold FX.2002.Parametric and nonparametricvolatilitymeasurement,In Handbook of Financial Econometrics,Hansen LP,Ayt-Sahalia Y,eds;NorthHolland:Amsterdam,forthcoming.
[13]Ebens,Heiko,2000,On Modeling and Forecasting Stock Volatility,Dissertation Abstracts International,Volume:62-02,Section:A,page:0697.;Advisers:Pedro de Lima;Tim Bollerslev.
[14]Oomen RC.A.,2001,Using High Frequency Stock Market Index Data to Calculate,Model&Forecast Realized Return Variance,www.panagora.com/2001crowell/ 2001cp_30.pdf.
[15]Bandi,FM and Russell,JR,2003,Microstructure Noise,Realized Volatility,and Optimal Sampling,http:// www.sess.smu.edu.sg/events/Paper/bandi.pdf.
[16]黄后川,陈浪南.中国股票市场波动率的高频估计与特性分析[J].经济研究,2003,(2):75-82.
[17]施红俊,马玉林,陈伟忠.实际波动率理论及实证综述[J].山东科技大学学报(自然科学版),2003,(3): 101-105.

