一端固定一端自由的受压杆件的拓扑优化

宋其伟，边炳传

(1.山东泰安恒基置业发展有限公司，山东泰安 271000;2.泰山学院建筑与机械工程系，山东泰安 271021)

1 引言

受压杆件的稳定问题(屈曲问题)即当细长杆件受到轴向压力的作用下会不会弯曲的问题.在进行杆件的结构设计时，不仅要考虑杆件的强度、刚度，还必须要充分地考虑到受压杆件的稳定问题.其中，一端固定一端自由的受压杆件是压杆稳定中的一种重要形式.当前，对受压杆件稳定的优化研究工作主要有:D.Manickarajah［1］等研究了考虑屈曲的杆件与框架的优化问题;郭旭等［2］研究了桁架在屈曲载荷约束下的全局稳定性拓扑优化;荣见华等［3］运用ESO方法研究了框架在承受最大临界屈曲载荷情况下的截面优化;彭兴黔［4］研究了两端弹性铰支约束下受压杆件稳定的优化设计，采用拉格朗日乘子法，求得受压杆件在弹性铰支约束下，截面优化分布规律和挠曲函数的表达式，并给出计算临界荷载的统一公式;邹文胜等［5］考虑压杆稳定性的桁架拓扑优化设计.综上所述，多数研究集中在了桁架的拓扑优化设计，只研究了桁架中受压杆件的去留问题，并未对具体受压杆件的拓扑结构进行优化设计.本文对一端固定一端自由的受压杆件稳定利用独立、连续、映射［6－7］的方法进行拓扑优化设计，取得了较为理想的拓扑优化结果.

2 建立受压杆件模型

受压杆件稳定的约束形式有多种，在本文中主要研究以一端固定，一端自由的大挠度受压细长杆件，在Patran软件平台上建立受压杆件的虚拟模型，受压杆件的截面半径为20mm，高度为1440mm的长圆柱，弹性模量E=210×103MPa，泊松比v=0.3，密度ρ=7.8×10－6kg/mm3，分布力P=20010N，作用于上端圆截面的节点上，由于上端圆截面施加分布力，所以顶层单元为保留单元，其余为设计区域.下边界采用固定支撑力，上端部施加分布力，划分3072个8节点体单元，基结构重量为13.75kg，如图1所示.

根据材料力学［8］压杆稳定的知识，可以得到屈曲临界力的大小为:P=n2π2EI/L2(n=0，1，2，…).

图1 有限元模型

如果，两端采用不同的铰支形式，且当n=1时，压力为最小值，则可以得到临界压力的欧拉公式普遍形式:Pcr=π2EI/(μL)2，其中，μ为长度系数.

利用有限元方法建立以临界力为约束受压杆件稳定的拓扑优化模型.其中以结构重量最小为目标，屈曲临界力为约束的连续体拓扑优化模型:

其中临界屈曲载荷由屈曲分析的特征值方程得到，屈曲分析的特征值方程为:

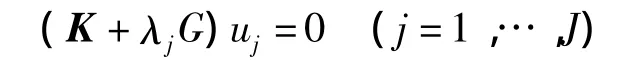
模型中的公式:fw(ti)，分别为单元重量、单元刚度阵、单元几何阵的过滤函数.公式中t为拓扑设计变量，a，b分别为幂指数，在本文中取a=1，b=3.3.

3 数学模型的求解

令a/b=β，则上式变为fw(ti)，目标函数变为:

由于目标函数是非线性的，对目标函数进行二阶泰勒近似展开，并略去常数项得到:

对优化模型中的约束进行处理，需要对约束进行泰勒展开，需要求临界屈曲力对xi求偏导数得:

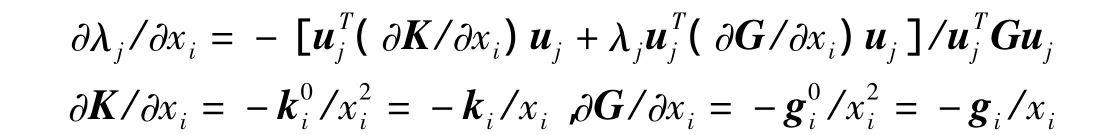
又因为屈曲临界力由下式表示:

而刚度阵与几何阵表示为:

临界屈曲力对xi求偏导数可以表示为:

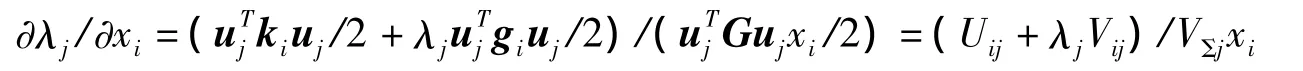
将约束用一阶泰勒展式近似展开:

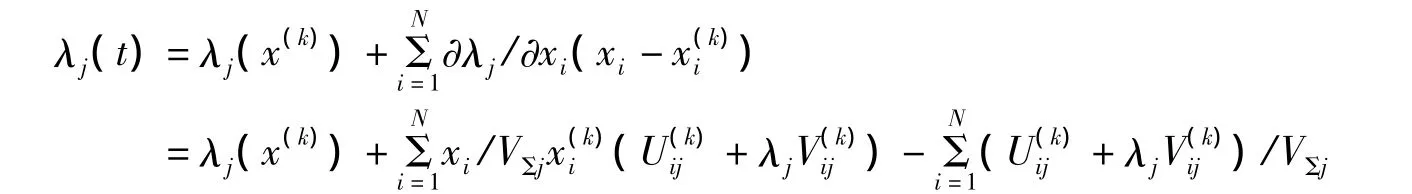
其中上标k指第k次迭代的值.

对λj≤约束有:

采用对偶理论将上述模型转化为对偶规划:

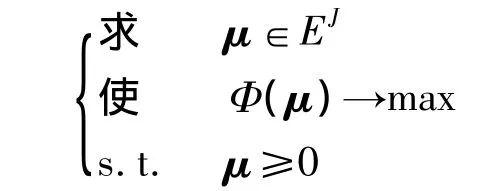
其中，W(k)及W(k+1)为前轮与本轮迭代的结构总重量，ε为收敛精度，本文取ε=0.001.

4 拓扑优化结构结果讨论

为确定临界屈曲载荷的上限，需要首先对结构进行屈曲分析.由于2阶、4阶屈曲模态分别与1阶、3阶相同，只是变形方向有所不同，所以在此只分别研究受压杆件的1阶、3阶、5阶的屈曲模态.对压杆模型进行屈曲分析，得到1阶屈曲因子ζ1=1.588，1阶屈曲临界力λ1=31775.88N;3阶屈曲因子ζ3= 14.301，3阶屈曲临界力λ3=286163.01N;5阶屈曲因子ζ5=39.776，5阶屈曲临界力λ5=795917.76N.

从图中可以看出，圆形截面的受压杆件在半径方向发生屈曲变形可能性是相同的，所以拓扑结构在圆周径向上具有一致性.拓扑结构在发生变形的端部材料去除比较多，产生瓶颈结构;同时发现1阶屈曲模态的拓扑结构中的挠曲线与两端铰支、长为2倍的压杆的挠曲线的上半部相同，验证了欧拉公式中的长度系数.

［1］D.Manickarajah，Y.M.Xie，G.P.Steven.Optimisation of columns and frames against buckling［J］.Computers and Structures，2000，75:45－54.

［2］X.Guo，G.D.Cheng，N.Olhoff.Optimum design of truss topology under buckling constraints［J］.Struct Multidisc Optim，2005，10: 158－162.

［3］J.H.Rong，Y.M.Xie，X.Y.Yang.An improved method for evolutionary structural optimisation against buckling［J］.Computers and Structures，2001，79:253－263.

［4］彭兴黔.两端弹性铰支约束下压杆稳定的优化设计［J］.华侨大学学报(自然科学版)，2002，23(1):45－49.

［5］邹文胜，左正兴，廖日东，文占科.考虑压杆稳定性的桁架拓扑优化设计［J］.北京理工大学学报，1999，19(1):29－33.

［6］隋允康.建模·变换·优化——结构综合方法新进展［M］.大连:大连理工大学出版社，1996.

［7］边炳传，隋允康.多约束作用下连续体结构的拓扑优化［J］.计算力学学报，2010，27(5)，781－788.

［8］刘鸿文.材料力学［M］.北京:高等教育出版社，1992.