我国农业内各业之间动态相互作用分析

王文智，武拉平

（中国农业大学经济管理学院，北京100083）

农业生产受到很多因素的影响，比如自然因素、市场因素和科学技术因素等。改革开放以来我国的农业结构发生了较大的变化，其中种植业占农林牧渔业总产值的比例由1978年79．3%降到2009年的52．71%，畜牧业在此期间发生变化程度较小，林业由1978年15．49%上升到2009年的33．53%，同时畜牧业也有较大的发展，占农林牧渔业总产值的比例由改革开放之初的1．64%上升到2009年的9．69%。陶红军等在对湖北农业各业关系的研究基础上认为农业作为一个特殊的产业，农业内各业间的发展具有高度的依赖性，协调产业发展才能使农业良性和可持续发展；［1］农业中的种植业、林业、畜牧业和渔业是相互作用和相互影响的，农业结构的变动对经济增长有着重要的作用，不同的产业结构带来不同的经济效益，［2］目前我国农业和农村经济发展已经进入了调整结构为主的主要的新发展阶段。［3］结构的变化有些是政策引导的，有些是产业发展和市场波动推动的，有些是理性的，有些是盲目的。［4］基于以上内容，对农业结构的内在规律进行综合深入研究非常有必要，目前对我国农业动态结构及农业内的各业的相互作用进行实证研究的较少。本文在建立的向量自回归模型的基础上，形成农业的动态结构方程，进而分析农业内各业的相互作用，可以准确掌握农业结构调整对整个农业内其他各业及整个农业当期和未来若干期的影响方式及影响程度，为农业结构调整的政策制定和实施提供参考。

一、研究方法

本文主要是在建立VAR（向量自回归）模型的基础上进行Granger因果关系检验，脉冲响应和方差分解，VAR模型是一种非结构化模型。［5］传统的结构化模型在描述经济变量之间关系以及处理具有动态特征 （及滞后期对当期有影响）的经济变量时，需要具有复杂的经济理论基础。然而，对于某些经济理论，特别是复杂系统，难以用一个结构化模型来描述变量之间的动态关系，而且在结构化模型中，内生变量既可以出现在方程的左端又可以出现在右端，使得参数估计和模型推断变得更加复杂。［6］为了解决这些问题，出现了一种用非结构方法来建立各个变量之间关系的模型，VAR模型就是经典的非结构化模型。本研究即基于VAR模型，深入分析农业内各业之间的动态相互作用。

（一）模型设定

VAR模型把系统中每一个内生变量作为系统中所有内生变量的滞后项的函数来构造模型，本研究中模型具体形式为：

其中yt是 （n×1）向量组成的同方差平稳的线性随机过程，yt-i（i＝1，2，…，p）是滞后期内生变量，p是自回归滞后阶数，At为 （k ×k）的系数矩阵，α是k维常数项向量，εt是由k维随即误差构成的向量，满足E（εt）＝0，E（εtyt-i）＝0，i＝1，2，…，p。在经济分析中，yt可以是原始经济变量序列，也可以是其差分序列，即变化率。

（二）变量选择与数据来源

本文分析农业、林业、畜牧业和渔业之间的动态关系，因此变量为前述各业的指数值，其中农业主要指种植业，数据来源为1978～2009年中国统计年鉴产值指数表示的各业的产出，其中以1978年为基期，［7］四个变量分别用AGRI，FORES，LIVS和FIRS表示，为了消除数据的异方差和因数据变化带来的剧烈变动，对各个变量取对数，DLNAGRI，DLNFORES，DLNLIVS和DLNFIRS表示对取对数后的变量进行一阶差分。

（三）变量单位根检验

在模型估计之前，首先利用ADF单位根检验法对数据的平稳性进行检验。检验结果下表1所示，三个变量原序列不平稳，一阶差分后平稳，因此所有的序列均为I（1）。

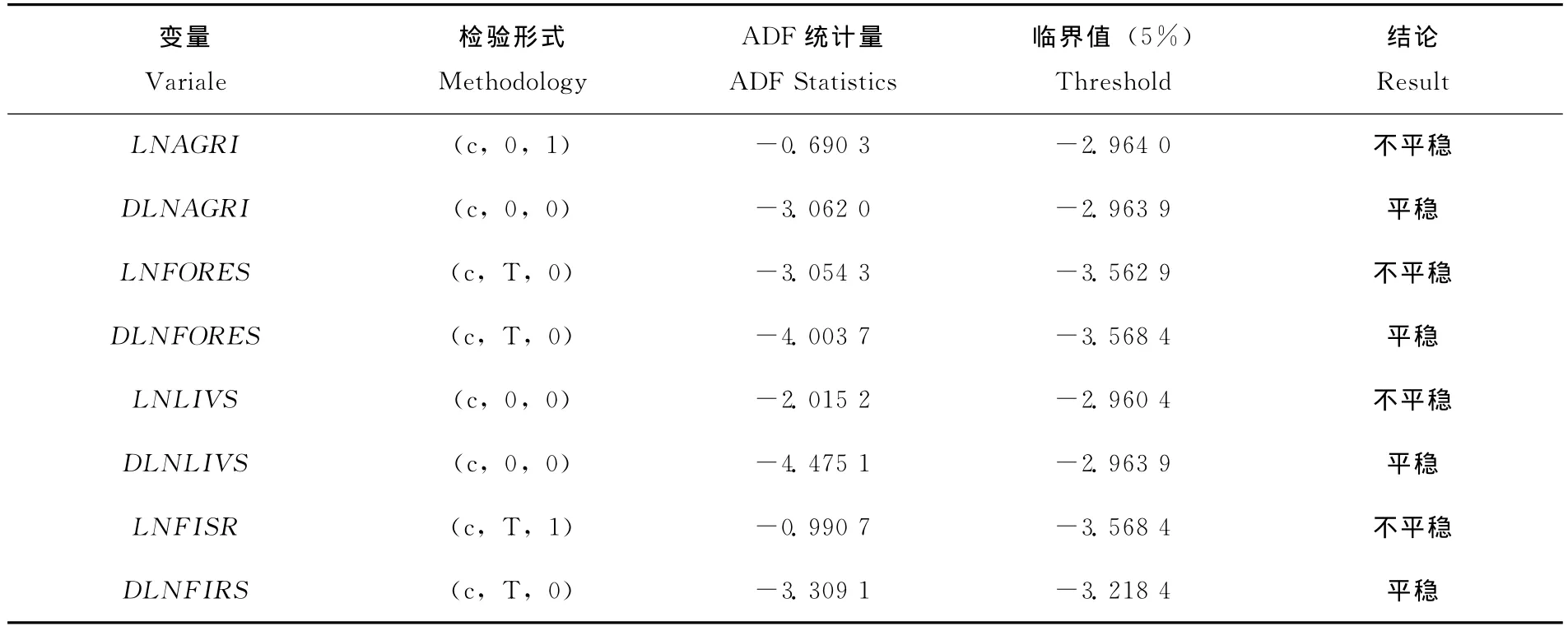
表1 变量平稳性检验结果Table 1 The Result of ADF Test

二、农业结构动态模型估计与检验

由以上单位根检验可知四个变量序列均是Ⅰ（1），VAR模型的建立是基于平稳序列，所以将变量通过差分变为平稳序列，因变量yt＝ （DLNAGRI，DLNFORES，DLNLIVS，DLNFIRS）1。在建立VAR模型之前，进行最佳滞后阶数的确定。如表2所示为最佳滞后阶数分析结果，EPE，SC，HQ标准所确定的最佳滞后阶数为3阶，根据多数原则选择3阶作为模型的最佳滞后阶数。

（一）农业动态结构的估计结果及模型稳定性检验

按照上述所确定的3阶滞后阶数进行VAR模型估计，在估计结果中进行模型稳定性检验，如图1所示，所有的AR特征多项式的逆根都在单位圆内，回归残差序列满足正态性，不存在相关性和异方差，是平稳系统模型。

表2 VAR模型最佳滞后阶数选择指标值Table 2 Numbers of Lags of VAR Model

农业动态结构估计结果如下：

图1 VAR（8）的AR特征多项式逆根图Fig．1 Inverse Roots of AR Characteristic Polynomial

四个方程的决定系数分别为0．475，0．542，0．798和0．743，拟合程度较高，约70%的系数通过了5%的显著性水平检验，由结果可以看出不同滞后阶数对当前产值指数的影响方向会发生变化，系数矩阵中对角线表示各业自身滞后期对其影响，影响大部分为正向，因此各业自身的产值增加具有连贯效应。

滞后一期的农业对其他各业均会发生促进的作用，但是滞后大于一期时，均会对其他各业产生反向的作用，即上期农业产业的发展促进农业自身、林业、畜牧业、渔业的发展，［8］主要是农业可以为此提供原材料，但是这种促进作用不会在各滞后期都发生，因为在一定程度上各业之间也存在着一种资本、劳动力等生产要素的竞争性。林业的发展几乎在各期都会促进农业中其他业的发展，林业的发展一方面可以改善自然环境，另一方面林业发展提供的林产品可以为种植业、畜牧业和渔业提供生产要素；系数矩阵第三列均为负数，因此畜牧业的发展对其他各业产生负的作用，可能原因为畜牧业在土地和劳动力上和其他各业形成直接的竞争关系。渔业作为农业中不可或缺的业态，尽管在农业中所占比例较小，其发展也会促进整个农业的协调发展。［9］此外，随着滞后期的增加，系数矩阵中数值变小，因此随着滞后期的增加，对当前各业产值的影响减小，符合预期。

（二）Granger因果关系检验

在VAR模型估计的基础上，进行Granger检验，检验结果如下表3所示。

表3 VAR Granger因果关系检验结果Table 3 Results of Granger Test in VAR Model

从表3的因果关系检验结果可以得出以下结论：

1．林业和畜牧业，畜牧业和渔业存在双向的Granger因果关系。畜产品和渔业产品存在一定的替代关系，因此会相互影响；畜牧业尤其是牛羊等对草地有较大的需求，其发展会与林业的发展在土地要素上形成竞争，［10］形成了双向的因果关系。

2．农业和渔业，林业和渔业不存在Granger因果关系。总体上说农业和林业以及林业和渔业之间的依存度较小，［11］因此彼此之间不存在相互影响。

3．农业和林业，农业和畜牧业存在单项的Granger因果关系检验。农业是林业产值变化的Granger原因，农业发展的一个方面是扩大种植面积，会影响林业的发展，同时其产量会直接影响到农产品的供给，进而影响到畜牧业的发展。［12］

（三）农业、林业、畜牧业和渔业脉冲响应函数

脉冲响应函数描述了来自某个随即扰动项的一个标准差冲击 （称之为 “脉冲”）对模型变量当期和未来取值的影响，它能够形象的刻画出变量之间动态作用的路径变化。通过脉冲响应函数可以检验农业、林业、畜牧业和渔业在分别受到外界冲击时对其他各业的影响强度和持续的时间。

图2至图5分别是农业、林业、畜牧业和渔业产值指数对数值一阶差分对来自自身及其他三个行业每一单位正向标准差新息冲击后的脉冲反应图形。随着时期数的增加，新息产生的影响逐渐减小。

来自农业的新息会对农业产值当期产生大的影响，来自林业和畜牧业的新息冲击在第2期才会影响到农业产值，渔业新息冲击在第3期才会对农产产值产生影响，但是总体上各业新息的冲击对农业产生的影响在第9期趋于0；农业对来自自身、林、牧、渔业新息冲击的最大反应按照绝对值从大到小顺序依次为：自身＞林业＝渔业＞畜牧业 （如图2）。

图2 DLNAGRI对冲击的脉冲响应Fig．2 Reponse of DLNAGRI to Cholesky One S．D．Innovations

来自农业和林业的新息冲击在当期即会对林业产值产生影响，畜牧业和渔业的新息冲击在第2期产生影响，但是总体上各业新息的冲击对林业产生的影响在第10期趋于0；林业对来自农业、自身、牧、渔业新息冲击的最大反应按照绝对值从大到小顺序依次为：自身＞畜牧业＞农业＞渔业 （如图3）。

图3 DLNFORES对冲击的脉冲响应Fig．3 Response of DLNFORES to Cholesky One S．D．Innovations

来自农业、林业和畜牧业的新息冲击在当期就对畜牧业产值产生影响，渔业新息冲击在第2期对畜牧业产值产生影响。各业新息的冲击对畜牧业产生的影响在第15期趋于0；畜牧业对来自自身、农、林、渔业新息冲击的最大反应按照绝对值从大到小顺序依次为：农业＞自身＞林业＞渔业 （如图4）。

来自各业的新息冲击在当期均对渔业产值产生影响，在第11期这种影响趋于0；渔业产值对来自自身、农、林、牧新息冲击的最大反应按照绝对值从大到小顺序依次为：自身＞农业＞林业＞畜牧业 （如图5）。

（四）农业、林业、畜牧业和渔业预测方差分解

方差分法是把系统中每个内生变量的波动按其成因分解为各个内生变量相关联的组成分，即分析每个新息冲击对内生变量变化的贡献度，从而了解各新息对模型的内生变量的相对重要程度。从Granger关系检验的结果中可知只有畜牧业会同时受到其他三个变量的影响，因此对变量畜牧业产值指数进行方差分解，以考察新息冲击之后各期以及稳定后农业、林业、畜牧业和渔业各自对畜牧业的影响程度。［13］

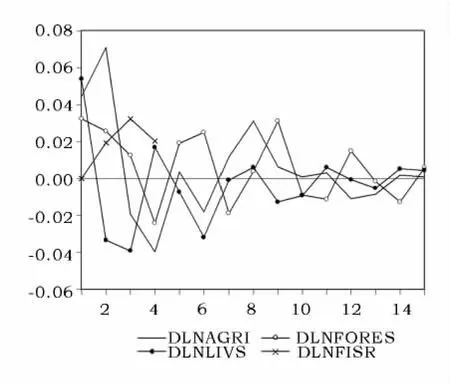
图4 DLNLIVS对冲击的脉冲响应Fig．4 Response of DLNLIVS to Cholesky One S．D．Innovations

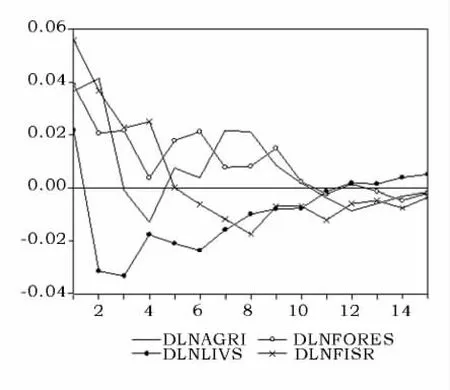
图5 DLFISR对冲击的脉冲响应Fig．5 Response of DLFISR to Cholesky One S．D．Innovations

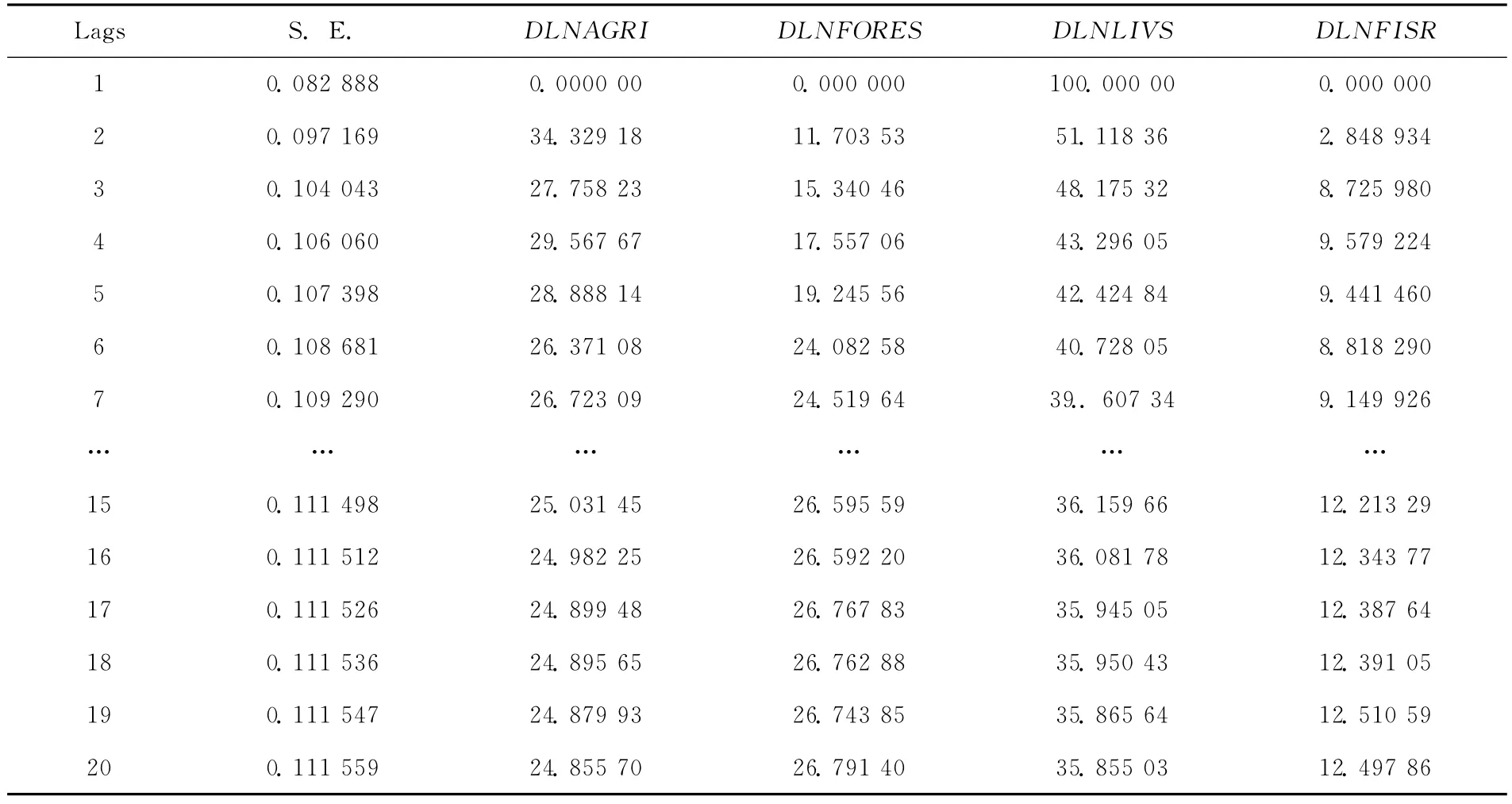
表4 对DLNLIVS进行方差分解结果Table 4 Variable Decompostion of DLNAGRI

从表4可以看出，在第1期畜牧业产值只受到自身扰动的影响，第2期自身扰动的影响则迅速降低到51．12%，农业、林业和渔业对畜牧业开始产生影响，在随后的时间内自身扰动对畜牧业产值的影响持续下降，其他各业冲击对畜牧业的影响程度增加，方差分解在第16期趋于稳定，此时畜牧业产值波动中36．08%由自身扰动引起，26．59%由林业新息冲击引起，仅次于自身扰动的影响，农产新息冲击对畜牧业扰动的影响可达到24．98%，渔业新息冲击对畜牧业扰动的影响程度最小为12．34%。由此可见畜牧业除去要保证自身发展的连续性外，在很大程度上也依赖林业和农业的发展。［14］

三、结论

在利用农业内各业产值指数建立VAR（3）模型基础上进行各业之间的Granger因果关系检验、脉冲响应和方差分解，得出了本文的以下三个研究结论。

第一，农业内部中林业和畜牧业产值波动比较容易受到其他各业的影响，其他各业对农业产值的影响不显著，由于畜牧业与渔业之间产品的替代性，二者之间相互影响显著；因为我国农业基本上受到政策的影响较大，其发展表现出一定的独立性，林业产值表现出一定的被动性，［15］畜牧业在很大程度上依赖农业和林业为其提供生产要素，渔业与其他各业在生产方式等方面有很大不同，不容易受到其他各业的影响。

第二，农业、林业、畜牧业和渔业分别对其他各业的新息冲击脉冲响应函数不同，初期对新息的冲击反应均较为强烈，随着时期数的增加，反应函数逐渐减小，直至最后趋于原有的水平，各业趋于新息冲击前的水平所需时期数不同。

第三，农业、林业和渔业产值均是畜牧业产值的Granger原因，畜牧业产值变化的预测方差主要由自身扰动引起，同时林业和农业值扰动的影响各约1／4，而渔业产值扰动对其的影响仅仅为12．34%；因此农业内部各业的发展越来越依靠农业内各业之间的共同发展，即要体现发展的协调性。［16］

［1］陶红军，陈鸿鸣，赵亮．基于VAR模型的农业各台动态关系分析——以湖北省为例 ［J］．华中农业大学学报 （社会科学版），2008（1）：20-23，27．

［2］穆维松，何有缘，王海燕，等．我国农业结构调整效应的计量分析 ［J］．农业现代化研究，2004（5）：186-189．

［3］李昕．我国粮食安全与农业结构调整取向：观照国际经验 ［J］．改革，2011（8）：67-76．

［4］卢布，陈印军，吴凯．我国农业结构现状及未来变化趋势研究 ［J］．农业技术经济，2005（2）：52-57．

［5］高铁梅．计量经济分析方法与建模——Eviews应用及实例［M］．北京：清华大学出版社．2009．5：300-311．

［6］吴凯，卢布，袁璋．石家庄市农业系统的经济结构及其模拟 ［J］．农业系统科学与综合研究，2005，21（2）：97-99．

［7］李成贵．中国农业结构的形成、演变与调整［J］．中国农村经济，2009（5）：18-24．

［8］李春海，张文，彭牧青．农业产业集群的研究现状及其导向：组织创新视角 ［J］．中国农村经济，2011（3）：49-58．

［9］张军．现代农业的基本特征与发展重点 ［J］．农村经济，2011（8）：3-5．

［10］张冬平．我国农业结构非效率分析［J］．统计研究，2003（5）：25-28．

［11］张冬平，袁飞．农业结构效率的数据包络分析 ［J］．农业技术经济，2001（3）：5-7．

［12］张开华．WTO框架下农业结构战略调整的若干思考［J］．农业经济问题，2001（7）：16-19．

［13］许朗，杨向阳．结构调整与农业发展［J］．农业经济，2005（8）：31-33．

［14］孔祥智，原梅生，黄志建．我国农业结构调整的历史机遇与策略 ［J］．山西财经大学学报，2001（2）：55-60．

［15］张燕．浅析我国农业结构调整［J］．安徽农业科学，2007．34（7）：1438-1439．

［16］倪洪兴．统筹两个市场两种资源，确保农业产业安全［J］．中国农村经济，2011（5）：57-60，81．