定向井抽油杆柱空间形态的计算方法

狄勤丰，王文昌，胡以宝，姚建林

(1.上海大学上海市应用数学和力学研究所，上海 200072;

2.上海大学上海市力学在能源工程中的应用重点实验室，上海 200072)

定向井抽油杆柱空间形态的计算方法

狄勤丰1，2，王文昌1，2，胡以宝1，2，姚建林1，2

(1.上海大学上海市应用数学和力学研究所，上海 200072;

2.上海大学上海市力学在能源工程中的应用重点实验室，上海 200072)

以曲率半径法描述井眼轨迹的空间形态，从空间杆单元入手，建立细长杆的有限元模型，并考虑井眼轨迹多支点的几何约束，以迭代法循环求解每一结点抽油杆柱的空间载荷及变形，再结合细长杆的屈曲模型，分析比较不同位置安放扶正器后抽油杆柱空间构形的变化。结果表明，通过计算实际井眼轨迹中抽油杆柱的三维受力及变形屈曲状态，能够判断扶正器安放的合理性，掌握杆柱的工作状况，预测杆/管偏磨位置。

抽油杆柱;计算方法;空间形态;径向位移;间隙

具有空间柔性变形特征的抽油杆柱在井下受油管约束，其空间形态具有多支点几何约束特征并随井深变化。由空间形态判断的杆-管接触状况决定着抽油杆柱扶正器的安放策略。目前的抽油杆柱数值模拟方法通过抽油杆柱与井眼轴线同轴的假设来简化未知量［1-5］，因而无法得到抽油杆柱在井下的空间构形特征。笔者通过有限元法及结点迭代法求解抽油杆柱的结点空间特征，并通过结点载荷判断抽油杆柱的失稳状态，进而以结点间的位移模式及屈曲模型求解抽油杆柱在结点间的变形状态，从而比较全面、准确地描述抽油杆柱在井下的空间形态，确定杆-管的接触状况，分析合理的扶正器安装方式，为抽油杆柱的防偏磨技术及杆柱动力学的进一步研究奠定基础。

1 井眼轨迹描述

假设井眼测段内的井眼轨道在垂直剖面图和水平投影图上均为圆弧，根据曲率半径法［6］，则有

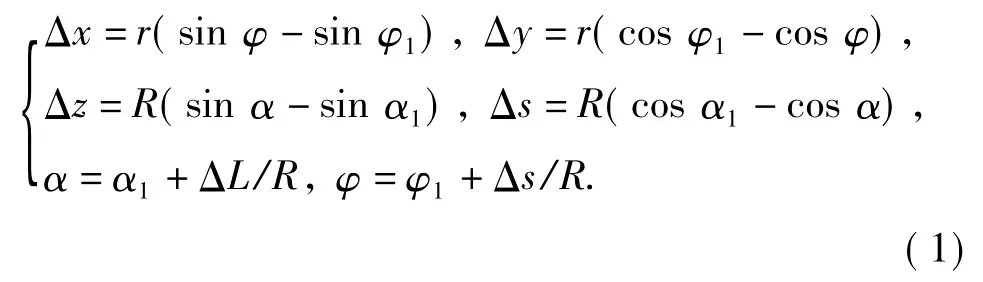
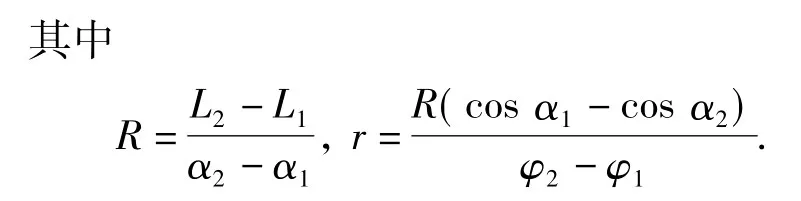
式中，R和r分别为井眼螺线在垂直剖面图和水平投影图上的曲率半径;α为井斜角，rad;φ为方位角，rad。在两测点L1、L2之间插值，对于不同的井斜角和方位角特征，R和r的计算公式略有差异。

根据微分几何的基本原理，对于任一空间曲线，有其一般参数表示式：r=r(s)，则其曲率k(s)和挠率τ(s)的计算公式为

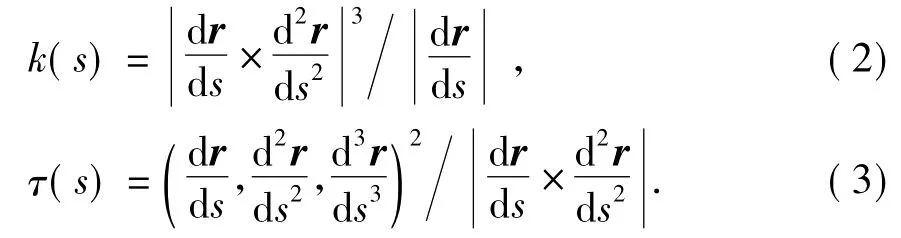
2 有限单元法模型

2.1 模型建立

抽油杆柱的有限元控制方程［7］为

式中，K为抽油杆柱的整体刚度矩阵;U为杆柱整体位移矩阵;F为杆柱整体外力矩阵。

单元位移矩阵为

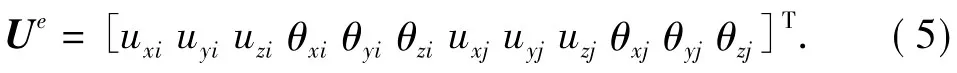
式中，ux，uy，uz为结点位移;θx，θy，θz为结点的扭转角;下标i，j分别对应单元的两端结点。

局部坐标系下细长杆单元刚度矩阵Ke［8］可表示为

单元结点杆端力矩阵为

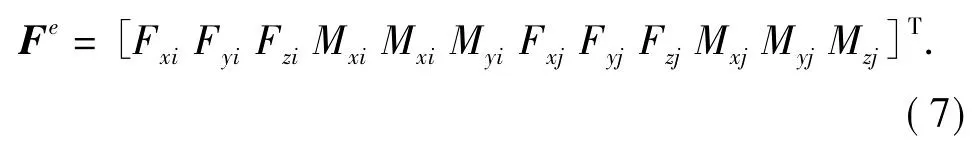
式中，Fx，Fy，Fz为结点载荷;Mx，My，Mz为相应方向的扭矩。

通过结点迭代法和直接约束法［8］，以求解出的结点位移作为已知条件，在杆柱不失稳时可以利用位移型函数推导出结点之间的径向位移模型，

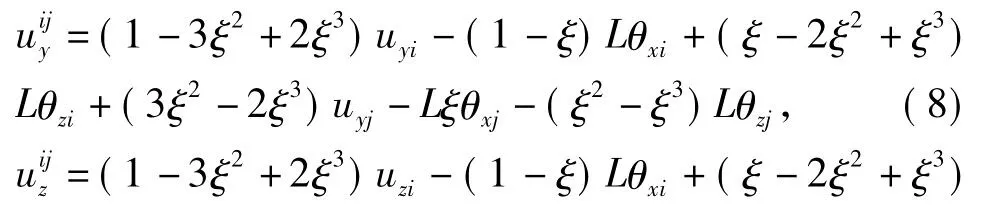
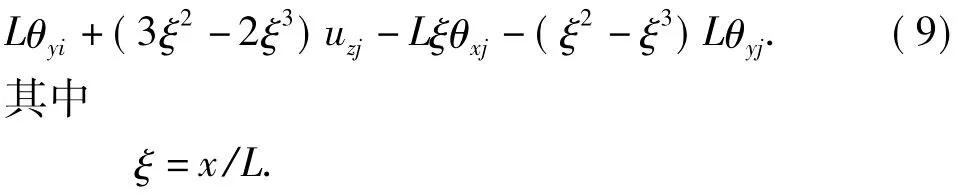
式中，x为距单元结点i端的距离，m;L为单元杆长，m。

2.2 屈曲模型

抽油杆柱在下部受到压缩载荷可能发生失稳，其在油管内的无因次屈曲方程［9-10］为

式中，θ为杆柱截面相对于油管的偏转角，rad;q为杆柱单位长度质量，N/m;r1为油管截面圆心到杆柱圆心的距离，m;EI为杆柱刚度，N·m2。

利用龙格－库塔及打靶法求解方程(10)，再进行变量代换，得到抽油杆柱在油管内的屈曲构形。

2.3 计算流程

计算流程如图1所示。

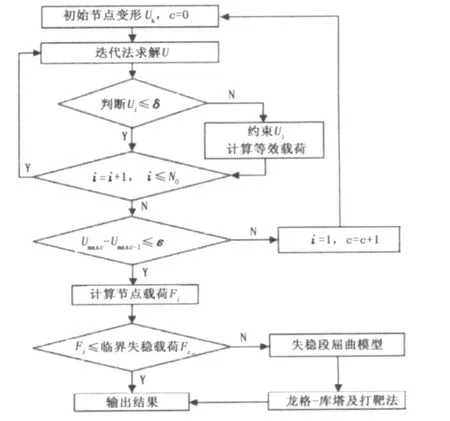
图1 迭代计算流程Fig.1 Iterative calculation flowchart

通过结点迭代法求解具有超长细比的抽油杆柱有限元方程(4)，利用直接约束法处理多支点的杆－管动态接触问题，其求解过程建立在结点循环(外循环)及稳定循环(内循环)的基础上。在结点循环中包含了结点步长的离散过程。然后通过结点载荷判断抽油杆柱的失稳状态，以龙格－库塔法求解屈曲模型。其中c为计算次数，N0为结点总数。

3 实例计算

沙26-1井为一定向井，泵深为1.7422 km，造斜点在井深1.1 km左右，泵型为Φ38 mm一级泵，油管内径为0.073 m。抽油杆柱组合为4级杆：Φ25 mm×96.53 m+Φ22 mm ×695.81 m+Φ19 mm×797.33+Φ16 mm×152.51 m。抽油机冲程为2.5 m，冲次为6次/min。井眼轨迹如图2所示。

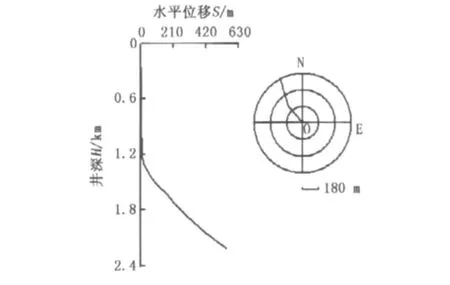
图2 沙26-1井井眼轨迹Fig.2 Deviation well path of Sha26-1

抽油杆柱在液体中的浮重为38.29 kN，当顶端集中载荷取运动周期内最小值35.96 kN时，抽油杆柱的轴向位移及轴向载荷如图3所示。

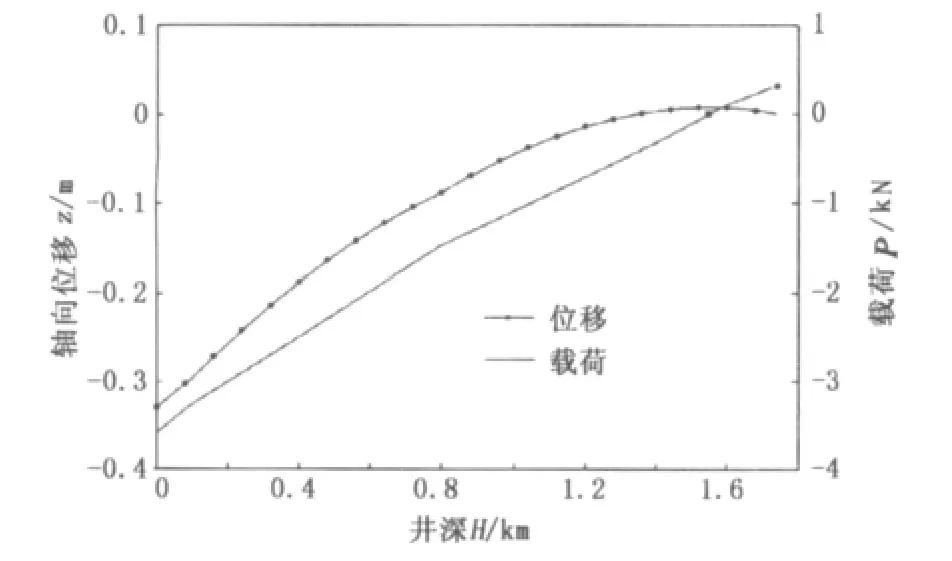
图3 沙26-1井杆柱轴向位移、载荷分布Fig.3 Axial displacement and load distribution of sucker rod strings of well Sha26-1

从图3中可以看出，抽油杆柱在承受最小载荷时，下部杆柱处于轴向受压状态，中和点位置在井深1.546 km处。最下端受轴向压力3.177 kN。整体坐标系¯x轴以重力方向为正。

抽油杆柱的y方向(高边方向)位移和z方向位移见图4。图4中显示了整个井段以每4 m为单元的计算结点的径向位移曲线以及从杆/管接触点开始添加扶正器后的抽油杆柱结点径向位移曲线。从图4中可以看出，杆柱在顶端集中载荷的状态下，上部基本保持在井眼的轴线附近，但由于定向井井眼轨迹的特征，造斜点下方大部分杆柱(1.244～1.740 km)都与油管接触。图4中z方向位移很小。

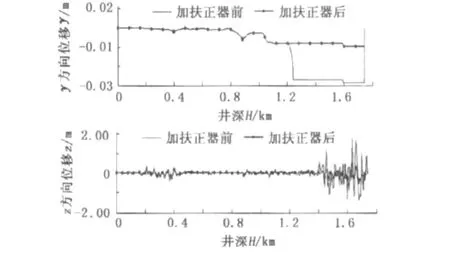
图4 沙26-1井杆柱结点位移Fig.4 Displacement of sucker rod strings nodal point of well Sha26-1

在实际作业中，为了减少抽油杆柱的磨损，常常在中和点以下杆柱以下密上疏的原则添加扶正器，但从图4中可以发现，由于中和点位于接触点下方，所以这一原则并不适合泵挂较深的定向井，这也是造成定向井抽油杆柱扶正器添加方法仍值得探讨的原因之一。本文中主要针对抽油杆柱的三维空间形态进行计算，对这一问题不加探讨，仅仅是为了比较扶正器添加造成的变化，对比了根据欧拉失稳条件添加扶正器及假设在1.244～1.736 km的杆柱上每4 m添加一个扶正器的径向位移。计算结果见杆柱局部(1.6～1.625 km)放大图(图5)。

从图5中可以看出抽油杆柱轴线在油管中的变形，在不考虑扶正器作用时，抽油杆柱在重力作用下靠在油管内壁，由于下部受压，在此井段内发生正弦屈曲。以欧拉失稳条件为依据进行变间距扶正器添加时，能够限制杆柱的径向位移不与油管发生接触。以等间距(4 m)添加扶正器时，杆柱在下部受压段的径向变形仍然会有局部点与油管发生接触。所以，根据抽油杆柱的径向位移变化能够判断扶正器添加方式是否合理。

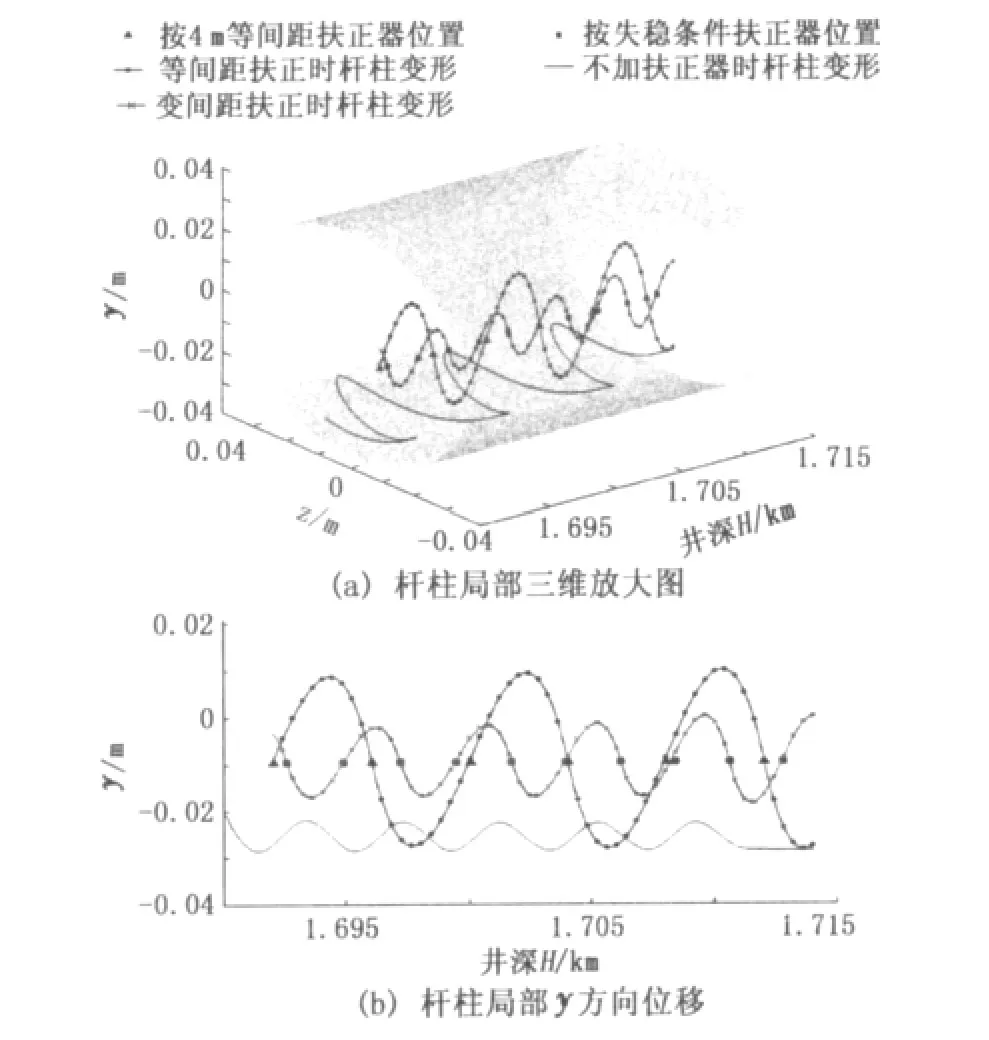
图5 沙26-1井杆柱局部三维放大图和y方向位移曲线Fig.5 Detail view of partial sucker rod strings and displacement of y direction of well Sha26-1

4 结论

(1)以抽油杆柱在井眼中居中为假设条件的数值仿真模型无法求解杆柱在井眼中的空间构形。利用有限元法，选择合理的迭代计算方式及边界条件，可以较为精确及快速地计算抽油杆柱在井眼中的纵、横变形状态，克服了一直以来以居中为假设条件建立模型的局限性。

(2)非线性刚度矩阵的影响主要体现轴向参数与径向参数的耦合作用，否则径向位移计算结果将不受轴向载荷变化影响。在直井中适用的中和点下以下密上疏原则添加扶正器的方法在复杂结构定向井中不一定适用。

(3)抽油杆柱在井下的三维空间形态可以把握抽油杆柱在井下与油管的接触位置及变形状态，有效地判断扶正器添加是否合理。

［1］吴奇，刘合，王素玲.抽油机井抽油杆柱瞬态力学行为有限元分析方法［J］.中国机械工程，2005，16(22)：1991-1994.

WU Qi，LIU He，WANG Su-ling.Transient mechanical action finite element analysis method of sucker-rod strings in pumping well［J］.China Mechanical Engineering，2005，16(22)：1991-1994.

［2］杨海滨，狄勤丰，王文昌.抽油杆柱与油管偏磨机理及偏磨点位置预测［J］.石油学报，2005，26(2)：100-103.

YANG Hai-bin，DI Qin-feng，WANG Wen-chang.Prediction of serious abrasion position and mechanism of uneven abrasion between sucker rod strings and tubing［J］.Acta Petrolei Sinica，2005，26(2)：100-103.

［3］王文昌，狄勤丰，邹海洋，等.抽油杆柱三维力学分析及设计系统(DARS)的开发和应用［J］.钻采工艺，2008，31(1)：98-101.

WANG Wen-chang，DI Qin-feng，ZOU Hai-yang，et al.Development and application of the 3D design and analysis system for sucker rod strings［J］.Drilling ＆ Production Technology，2008，31(1)：98-101.

［4］EVERLTT T A，JENNINGS J W.An improved finitedifference calculation of downhole dynamometer cards for sucker-rod pumps［J］.SPE Production Engineering，1992，7(1)：121-127.

［5］张宏，刘海浪，孙应民.定向井有杆泵抽油系统的有限元分析［J］.石油学报，2000，21(6)：102-106.

ZHANG Hong，LIU Hai-lang，SUN Ying-min.FEM analysis of sucker-rod pumping system for directional well［J］.Acta Petrolei Sinica，2000，21(6)：102-106.

［6］刘修善，王珊，贾仲宣.井眼轨道设计理论与描述方法［M］.哈尔滨：黑龙江科学技术出版社，1993：46-49.

［7］王勖成，邵敏.有限单元法基本原理和数值方法［M］.北京：清华大学出版社，2002：460-475.

［8］王文昌，狄勤丰，姚建林，等.三维定向井抽油杆柱力学特性有限元分析新方法［J］.石油学报，2010，31(6)：1018-1023.

WANG Wen-chang，DI Qin-feng，YAO Jian-lin，et al.A new finite element method in analyzing mechanical properties of sucker rod strings in 3D directional welbores［J］.Acta Petrolei Sinica，2010，31(6)：1018-1023.

［9］ 高国华.油井管柱的屈曲和分叉［M］.北京：石油工业出版社，1995：50-53.

［10］ 陆佑方.柔性多体系统动力学［M］.北京：高等教育出版社，1993：330-333.

Calculation method of sucker rod strings space configuration in directional well

DI Qin-feng1，2，WANG Wen-chang1，2，HU Yi-bao1，2，YAO Jian-lin1，2
(1.Shanghai Institute of Applied Mathematics and Mechanics，Shanghai University，Shanghai 200072，China;2.Shanghai Key Laboratory of Mechanics in Energy and Environment Engineering，Shanghai University，Shanghai 200072，China)

The wellbore trajectory was described by the radius of curvature method，and a finite element model of slender rod was established and solved by the curnode iterative method.The node force and deformation of sucker rod strings also could be obtained by this method with the consideration of multi-supports geometric constraints.Then the differences of spatial configuration of rod strings with various fixation patterns of centralizer were compared.The results show that the eccentric wear position of sucker rod strings and fixation patterns of centralizer could be determined by the solution of 3D configuration of sucker-rod strings in wellbore.

sucker rod strings;calculation method;space configuration;radial displacement;clearance

TE 21

A

10.3969/j.issn.1673-5005.2011.03.014

1673-5005(2011)03-0072-04

2010－09－20

国家自然科学基金项目(50874071);上海市科委重点科技攻关计划(071605102);上海市教委科研创新项目(08ZZ45);上海大学研究生创新基金项目

狄勤丰(1963－)，男(汉族)，江苏溧阳人，教授，博士，博士生导师，主要从事石油工程和工程力学方面的研究。

(编辑 李志芬)