地层蓄热效应对输气管道数值模拟精度的影响

丁延鹏，李玉星，郝宏娜，毕研军

(1.中国石油大学储运与建筑学院，山东青岛 266555;2.中国石油天然气管道科学研究院，河北廊坊 065000)

地层蓄热效应对输气管道数值模拟精度的影响

丁延鹏1，李玉星1，郝宏娜1，毕研军2

(1.中国石油大学储运与建筑学院，山东青岛 266555;2.中国石油天然气管道科学研究院，河北廊坊 065000)

采用一维非等温天然气流动模型对高压天然气输送管线中的快瞬变流动进行数值模拟，研究地层蓄热效应对高压天然气快瞬变管流数值模拟精度的影响。从工程实际角度对质量、动量和能量守恒方程的基本变量进行等价变换，建立天然气管流与外界地层之间一维轴对称的非稳态传热模型，以BWRS状态方程为基础，采用特征线法对天然气管流的快瞬变过程数学模型进行数值求解，并与简化稳态模型数值结果进行对比。结果表明：国内常用的简化稳态传热模型过高估计了管线中流量的波动幅度，工程应用中应采用考虑地层蓄热效应的非稳态传热模型对高压天然气管流进行仿真模拟;非稳态模型和算法具有较高的准确性。

输气管道;快瞬变流;数值模拟;地层蓄热效应;特征线法

由于输气管道运行中存在着天然气的需求波动，需要进行阀门开关、压缩机启停、调压器调节等操作，因而输气管道往往处于不稳定的运行状态。投产时间长、腐蚀磨损严重的管网在阀门开关等操作过程中就存在着事故隐患，因此有必要对输气管道在阀门开关过程中的运行状况进行瞬态模拟分析。天然气管流的瞬态模拟是指对描述管内流体质量、动量和能量守恒以及状态变化的偏微分方程组进行数值求解。目前，国内外对天然气管流瞬态模拟的研究大都采用一维非稳态数学模型，国外的研究重点在于数学模型以及求解方法上的创新与改进，国内在此领域的研究则侧重于模拟仿真技术在输气管道设计运行中的应用。管流与地层之间的传热通过能量方程中的传热项进行表述，天然气管流模型中传热项的处理存在着两种极端情况：等温模型和绝热模型［1］。目前，介于等温与绝热模型之间的非等温传热模型应用比较广泛［2－4］，依据传热过程是否随时间变化分为稳态和非稳态两种。稳态非等温传热模型在我国的输气管道模拟仿真研究中处于主导地位。笔者在一维非等温天然气管流模型中加入地层蓄热效应，建立非稳态非等温传热模型，对阀门瞬时开关产生的快瞬变流进行数值模拟研究。

1 数学模型

1.1 气体管流瞬变模型

由于天然气管输系统中经常存在着由于需求波动以及系统控制装置(如阀门、压缩机和调压器等)调节等原因形成的动态管流，因此实际模拟须采用考虑到压力、温度和流量等突变的双曲型非等温天然气管流模型。包含质量、动量和能量守恒定律的描述天然气管道内一维可压缩流动的数学模型［5－6］如下：

式中，p为管道压力，Pa;w为气体流速，m/s;ρ为气体密度，kg/m3;x为管内轴向长度，m;u为比内能，J/kgh;h为气体比焓，J/kg。

上述天然气管流模型是一组以密度、压力和流速为基本变量的双曲型偏微分方程组，比较适用于管线参数发生突然变化的情况［1，7］。天然气工业中，气体流速的测量数据并不容易得到，而且密闭输送中标准工况下的体积流量或质量流量才是天然气输送过程常用的参数。因此，将质量、动量和能量守恒方程变换成以压力、标况体积流量和温度为基本变量的等价形式［9－10］：

式中，A为管道横截面积，m2;D为管内径，m;Qm为体积流量，m3/s;s为管道沿线高程，m;g为重力加速度，m/s2;λ为摩阻系数;t为时间，s;q为单位时间内单位质量的气体与外界环境间的传热量，kJ/(kg·s)。

方程(6)为管线内控制体内单位质量气体的能量守恒定律，其最后一项是管内气体与管道外界环境间的传热项，该项对上述模型求解气体参数影响较大［1，11］。

1.2 状态方程

考虑到方程组(4)～(6)的封闭性及内在变量间的水力热力关联，需加入状态方程。BWRS状态方程属于多参数状态方程，具有很宽的操作工况，对比温度可低至Tr=0.3，对比密度则可高达ρr=0.3，并可以用于计算含有CO2、H2S、N2等气体的体系，是目前最佳的天然气状态方程之一。BWRS状态方程可以将压力表达成温度和密度的显示函数［11］，即

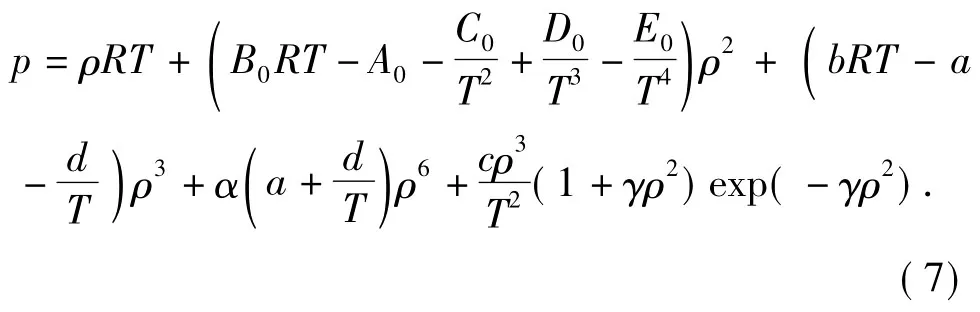
式中，T为系统温度，K;R为气体常数，J/(kg·K);A0、B0、C0、D0、E0、a、b、c、d、α、γ 为状态方程中的参数。

1.3 传热模型

在能量方程(6)中，传热项q代表着单位时间内单位质量的气体与外界环境间的传热量。对离散的管元，采用傅里叶法则计算气体和地层间的总传热量：

式中，K为传热系数，W/(m·K);Tamb为管道轴线两侧足够远处环境温度，K。

导热是天然气快瞬变管流中起主导作用的传热机制［12］，因此管道内沿轴向和环向的热传递可以忽略不计，只须考虑管壁和地层中的导热。通常的工程实践中，描述输气管道与外界地层间传热的模型通常是一维的，因为缺少描述管线沿线附近地层构造以及地层性质(温度、传热特性等)的准确数据，因此大都假定管道与外界地层间的热阻恒定，并进行简化稳态传热处理：假定管道周围地层的环境温度恒定Tamb不变。

将输气管道与外界地层间的传热项进行非稳态处理：由于压缩机出口管线的温度较高，对周围地层有一定加热效果，考虑到管道周围地层的蓄热效应，周围地层中会形成一个以管道为轴线的径向温度变化，如图1所示。

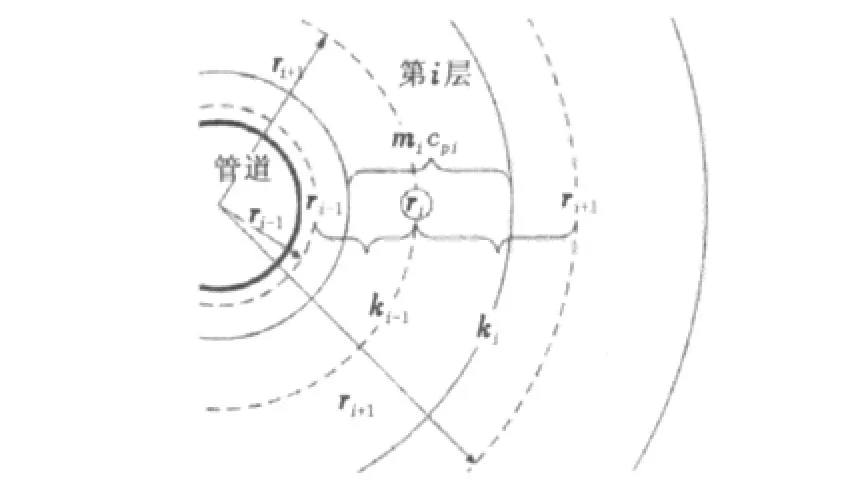
图1 非稳态传热模型离散示意图Fig.1 Dispersion diagram of unsteady heat transfer model

非稳态一维轴对称的径向传热过程用方程组表述为

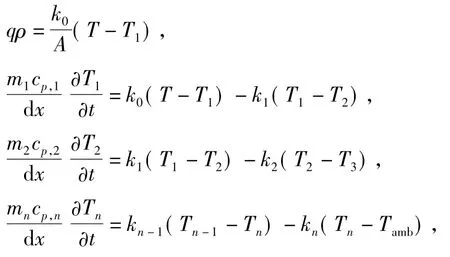
式中，n为管道周围地层传热区的离散元数目;mi为第 i层离散元的质量(i=1，…，n)，kg;cp，i为第 i单元的比定压热容，kJ/(kg·K);dx为管元长度，m;Ti为第i地层单元的温度，K;ki为第i－1层与第i层地层单元之间的传热系数，W/(m·K)。

在采用一维模型进行数值模拟的过程中，传热模型最少应含两层圆柱型传热层。假定不同地层离散单元的蓄热特性差别很大，时间常数也就不同，管道附近和远处的环境对温度变化的反应也分别有快有慢。非稳态传热过程中，考虑地层蓄热的初始条件设定为管道附近相邻地层单元之间的温度分布与简化稳态情况一致。

2 数值求解

采用的管流模型为一组双曲型偏微分方程组，因而采用特征线法进行数值求解。特征线法是求解二元一阶双曲型偏微分方程(组)的一类经典方法，其基本思想是先将基本方程组变换为沿特征线的常微分方程组，然后对常微分方程组结合初始条件和边界条件进行数值解。特征线法的优势是它可以处理模拟中的不连续性，比较方便地对边界条件进行处理，物理概念明确、数学分析严谨、计算精度较高［13］。

将方程组(4)～(6)采用特征线法进行基本变换之后得到沿轨线、顺特征线和逆特征线的3个特征方程：

沿轨线的特征方程为

式中，T0为管壁温度，K;as为音速，m/s。

方程组(9)～(11)是对原来的3个基本方程进行组合后得到的，因而已分不清连续性方程、动量方程和能量方程了，但它在整体上仍然与原来的基本微分方程组等价。采用以逆步进法为基础的有限差分法进行离散求解。离散网格如图2所示。在这个方法中解点A的位置通过网格划分确定。交于A点上的3条特征线向后延伸与前一时刻计算的一条线相交，以确定初始数据点G、M和H的位置。初始数据点上的流动参数用先前的解点进行插值获得。

图2 特征线法差分网格示意图Fig.2 Difference grid diagram of method of characteristics

3 算例

3.1 条件设定

采用Kiuchi提出的输气系统模型［2］对本文的模拟结果进行验证与分析。该系统如图3所示，包括一段长度为L=5 km、内径D=0.5 m的管线。地温Tamb=25℃，管内流体与管外地层间的总传热系数(包括管内流体与管壁间的对流换热、管壁内的导热以及管壁与紧贴管壁的第一层地层单元间的换热)K=2.84 W/(m2·K)。

图3 输气管道简图Fig.3 Diagram of gas transmission pipeline

式中，t为时间，min。

该模型通过入口处的流量与温度变化模拟压缩机出口阀门瞬时开关操作对管内参数的影响，通常用于检验管道快瞬变工况模拟算法的准确性。

本文中假定管道附近地层的各离散单元具有相同的热阻与热容。初始状态下，相邻地层单元之间的温度分布与稳态的情况一致。

3.2 模型算法对比验证

先用简化的稳态传热模型对上述输气系统进行模拟，并与Abbaspour计算结果进行对比，入口处流量模拟结果见图4。由图4可以发现，本文模型算法的结果与Abbaspour的计算结果［14］总体上比较吻合，证明了本模型及算法的准确性。

图4 模拟结果对比验证Fig.4 Comparison of simulation results

3.3 不同传热模型的模拟结果对比

采用考虑地层蓄热效应的非稳态传热模型，对Kiuchi输气系统进行了数值模拟，并将简化稳态传热模型与非稳态传热模型对入口流量的模拟结果进行比较，如图5、6所示。

图5 简化稳态与非稳态传热模型的模拟结果对比Fig.5 Comparison of simulation results using simplified steady and unsteady heat transfer model

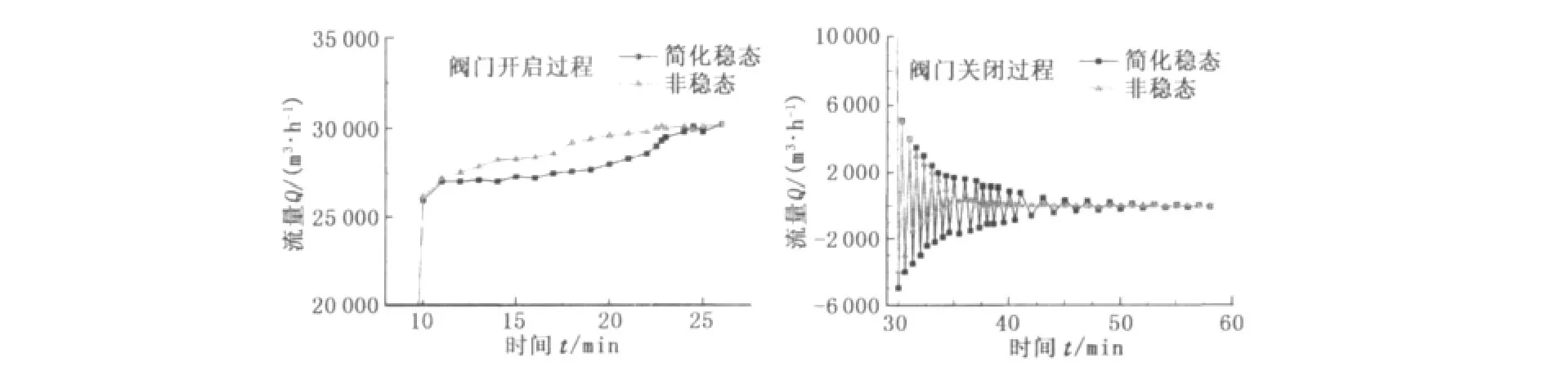
图6 阀门开关过程流量波动局部放大图Fig.6 Partial enlargement of flow fluctuation when opening/closing valve

从图6可以看出，阀门开启和关闭的模拟过程中，非稳态传热模型算得的流量比简化稳态传热模型的模拟结果更快地到达稳定状态，这可以通过地层的蓄热效应来解释。压缩机对气体的加热使得管内气体温度高于外界地层温度，对管外地层进行了加热，由于地层蓄热效应的存在，在输气管线周围形成了轴向温度梯度分布，地层温度的升高降低了管内气体温度的下降幅度，与简化稳态传热模型中设定外界地层温度不变相比，降低了计算过程中温度跳跃幅度，使得计算过程可以更快地到达稳定状态。这表明，考虑地层蓄热效应的非稳态模型可以显著增加流量曲线随时间变化的准确性。

4 结束语

将BWRS状态方程与一维非等温天然气管流瞬变模型耦合，采用特征线法对数学模型进行特征变换，应用逆步进法进行离散数值求解，验证结果说明该模型和算法具有较高的准确性。不考虑地层蓄热效应的稳态传热模型高估了管线中流量的波动幅度。工程应用中应该采用考虑地层蓄热效应的非稳态传热模型对高压天然气管流进行动态模拟。

［1］CHACZYKOWSKI M.Transient flow in natural gas pipeline：the effect of pipeline thermal model［J］.Applied Mathematical Modelling，2010，34(4)：1051－1067.

［2］KIUCHI T.An implicit method for transient gas flows in pipe networks［J］.Int J Heat Fluid Flow，1994，15(5)：378－383.

［3］THORLEY A R D，TILEY C H.Unsteady and transient flow of compressible fluids in pipelines：a review of theoretical and some experimental studies［J］.Int J Heat Fluid Flow，1987，8(1)：3－15.

［4］OSIADACZ A J，CHACZYKOWSKI M.Simulation of non－isothermal transient gas flow in a pipeline［J］.Archives of Thermodynamics，2001，22(1/2)：51－70.

［5］李玉星，姚光镇.输气管道设计与管理［M］.东营：石油大学出版社，2009：49－51.

［6］陈福来，帅健，冯耀荣，等.高压天然气输送管道断裂过程中气体减压波速的计算［J］.中国石油大学学报：自然科学版，2009，33(4)：130－135.

CHEN Fu－lai，SHUAI Jian，FENG Yao－rong，et al.Calculation of high－pressure natural gas decompression wave velocity during pipeline fracture［J］.Journal of China U－niversity of Petroleum(Edition of Natural Science)，2009，33(4)：130－135.

［7］吕巍然，王君苓，陈院生，等.一类非齐次微分方程解的增长性［J］.中国石油大学学报：自然科学版，2010，34(2)：166－174.

LÜ Wei－ran，WANG Jun－ling，CHEN Yuan－sheng，et al.Growth of solutions of some non－homogeneous differential equations［J］.Journal of China University of Petroleum(Edition of Natural Science)，2010，34(2)：166－174.

［8］ISSA R I，SPALDING D B.Unsteady one－dimensional compressible frictional flow with heat transfer［J］.J Mech Eng Sci，1972，14(6)：365－369.

［9］ POLONI M，WINTERBONE D E，NICHOLS J R.The calculation of pressure and temperature discontinuity in a pipe by method of characteristics and the two－step differential Lax－Wendroff methods［J］.ASME FED，1987，62：1－7.

［10］唐建峰，段常贵，吕文哲，等.特征线法在燃气管道动态模拟中的应用［J］.油气储运，2001，20(8)：12－17.

TANG Jian－feng，DUAN Chang－gui，LÜ Wen－zhe，et al.Application of the method of characteristics in dynamic simulation of gas pipes［J］.Oil＆ Gas Storage and Transportation，2001，20(8)：12－17.

［11］曹学文，陈丽，杜永军，等.超声速旋流天然气分离器的旋流特性数值模拟［J］.中国石油大学学报：自然科学版，2007，31(6)：79－86.

CAO Xue－wen，CHEN Li，DU Yong－jun，et al.Numerical simulation of swirling flow characteristics of supersonic swirling natural gas separator［J］.Journal of China University of Petroleum(Edition of Natural Science)，2007，31(6)：79－86.

［12］GREYVENSTEIN G P.An implicit method for the analysis of transient flows in pipe networks［J］.Int J Numer Meth Eng，2002，53：1127－1143.

［13］GATO L M C，HENRIQUES J C C.Dynamic behaviour of high－pressure natural－gas flow in pipelines［J］.Int J Heat Fluid Flow，2005，26：817－825.

［14］ ABBASPOUR M，CHAPMAN K S.Nonisothermal transient flow in natural gas pipeline ［J］.J Appl Mech Trans ASME，2008，75(3)：181－188.

Effect of underground heat capacity on numerical simulation accuracy of transient flow in natural gas pipelines

DING Yan－peng1，LI Yu－xing1，HAO Hong－na1，BI Yan－jun2
(1.College of Pipeline and Civil Engineering in China University of Petroleum，Qingdao 266555，China;2.China Petro ＆ Gas Pipe Research Institute，Langfang 065000，China)

One－dimensional，nonisothermal gas flow model was adopted to simulate the transient flow in high－pressure gas transmission pipelines.The effects of underground heat capacity on numerical simulation accuracy of fast transient flow in high－pressure natural gas pipelines were studied.From the engineering point of view，the basic variables of the mass，momentum and energy conservation equations were transformed equivalently.One－dimensional axial symmetry unsteady heat transfer model was established between natural gas pipe flow and the outside formation.The dynamic model based on the state equation of BWRS was solved by the method of characteristics.The results show that domestic simplified steady－state heat transfer model overestimates the fluctuation amplitude of flow rate in the pipeline，and the unsteady heat transfer model considering the effect of underground heat capacity should be used to simulate the transient flow in the practical high－pressure gas transmission pipelines.The unsteady－state model and the algorithm have high accuracy.

natural gas pipeline;fast transient flow;numerical simulation;underground heat capacity;method of characteristics

TE 832

A

10.3969/j.issn.1673－5005.2011.03.025

1673－5005(2011)03－0124－05

2010－12－06

国家自然科学基金项目(51074175);教育部新世纪人才支持计划(NCET－07－0847)

丁延鹏(1983－)，男(汉族)，山东烟台人，博士研究生，主要从事输气管道数值模拟研究。

(编辑 沈玉英)