一类对称广义中心对称矩阵反问题的最小二乘解

张 敏，刘丁酉

(1.武汉军械士官学校基础部，湖北 武汉 430075；2.武汉大学数学与统计学院，湖北 武汉 430072)

1 问题的提出

近年来，对于各类矩阵反问题AX=B的研究已取得了一系列的成果[1-2]，但由于实际问题中，获得的A与B的数据是有误差的，较难得到通解，因此研究问题的最小二乘解是有实际意义的.本文就机械振动设计中用到的一类对称广义中心对称矩阵[3-6]的最小二乘问题进行讨论.

本文用Rn×m表示n×m实矩阵集合，SRn×n表示n阶实对称矩阵集，ORn×n表示n阶正交矩阵集，0为相应阶数的零矩阵，AT与A+分别表示矩阵A的转置、Moore-penrose广义逆，‖·‖表示矩阵的Frobenius范数.对A=(aij),B=(bij)∈Rn×n，A*B表示A与B的Hadamard乘积，其定义为A*B=(aijbij)∈Rn×n.

定义1[3]设E,F是k阶实对称矩阵，u是k维实向量，P是k阶正交矩阵，α是实数，令:

则称R2k和R2k+1为对称广义中心对称矩阵.

所有n阶对称广义中心对称矩阵的全体记为SGCSn×n.

本文研究的问题如下：

问题Ⅰ 求X、B∈Rn×m，找A∈SGCSn×n，使得‖AX-B‖=min.

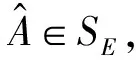
本文给出了问题Ⅰ的通解表达式，然后就AX=B，给出了解存在的充要条件及其通解的表达式，对问题Ⅱ证明了解的存在性，并给出了解的具体表达式.

2 问题Ⅰ的解

首先讨论SGCSn×n的结构.下文中的P均与定义中的所叙一致.

当n=2k时，令:

(1)

当n=2k+1时，令:

(2)

则D2k和D2k+1是正交矩阵.

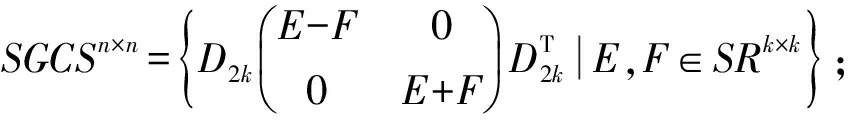
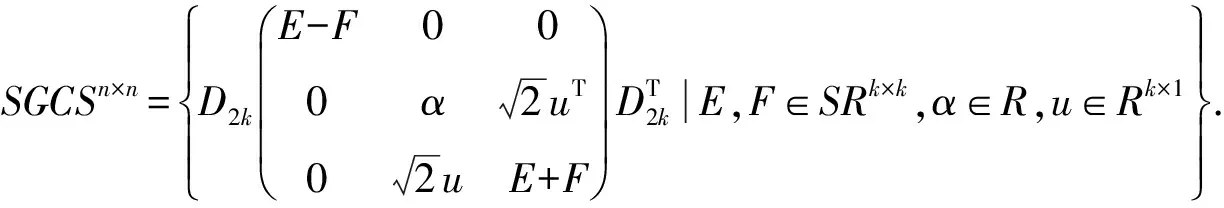
由此可见，无论n是偶数还是奇数，SGCSn×n的矩阵的一般形式为：

(3)

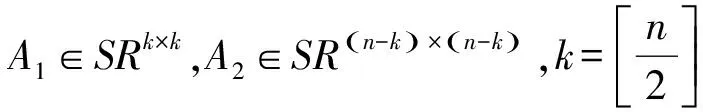
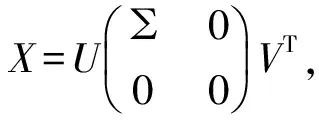
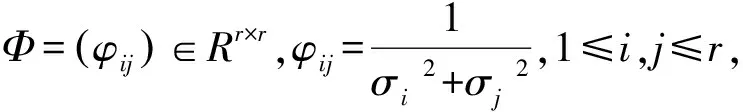
1)S1={A∈SRk×k|‖AX-B‖=min}可表示为：

2)S2={A∈SRk×k|AX=B}非空的充要条件是：B=BX+X,XTB=BTX,

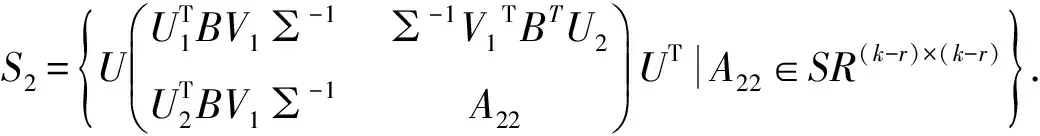
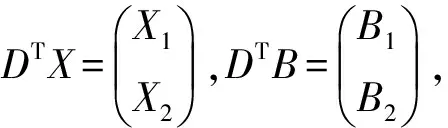
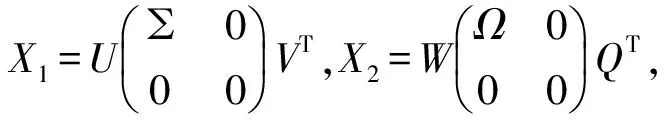
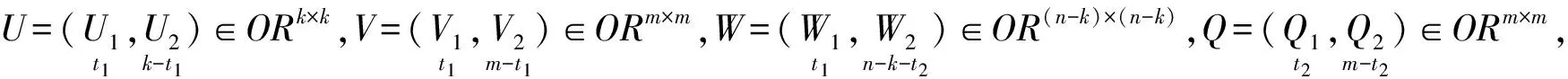
∑=diag(σ1,σ2,…,σt1)>0,t1=rank(X1),Ω=diag(d1,d2,…,dt2)>0,t2=rank(X2).

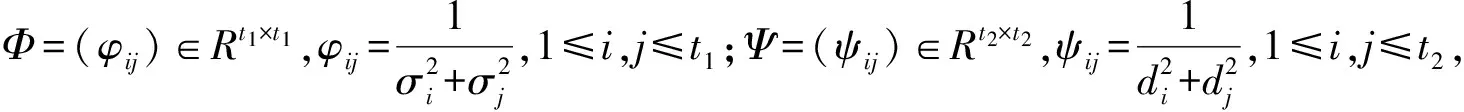
则问题Ⅰ的解集合为：

(4)

其中:

∀E∈SR(k-t1)×(k-t1)，

(5)

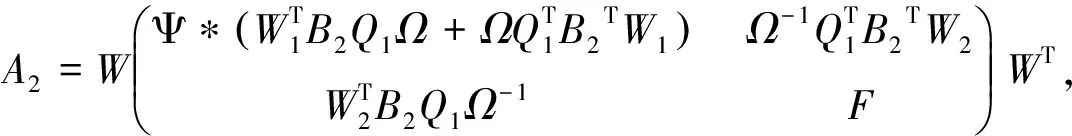
(6)

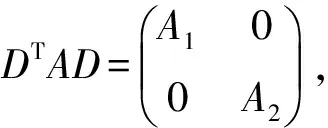
即‖AX-B‖=min等价于：

‖A1X1-B1‖=min和‖A2X2-B2‖=min.

(7)

由引理2知式(7)的解由式(5)、(6)表出，将其代入式(3)，则得解集合为式(4).

推论1 符号与定理1相同，则问题Ⅰ中AX=B有解的充要条件是：

Bi=BiXi+Xi,XiTBi=BiTXi(i=1,2)，

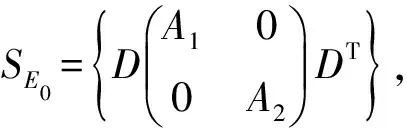
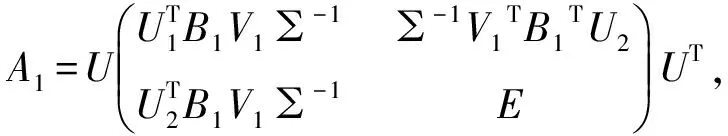
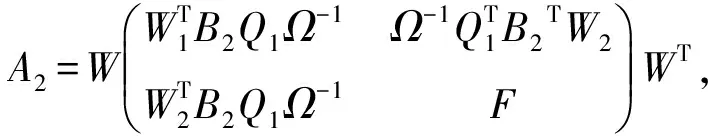
3 问题Ⅱ的解

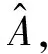
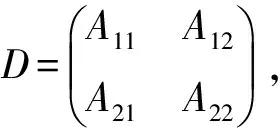
(8)

其中：

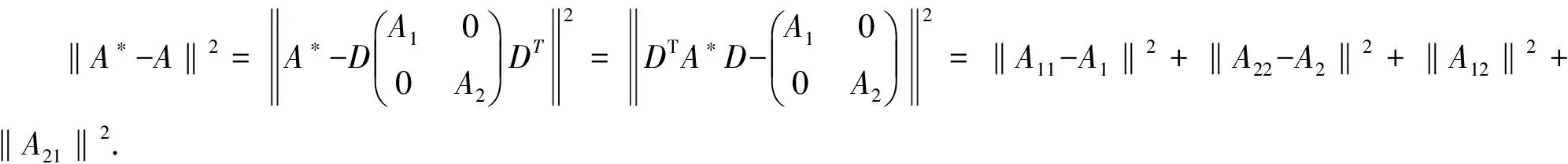
所以‖A*-A‖=min等价于：

‖A11-A1‖=min和‖A22-A2‖=min

(9)

由定理1中式(5)知：

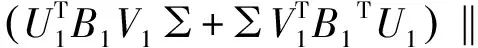
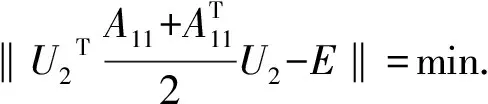
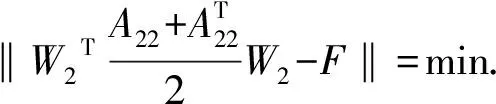
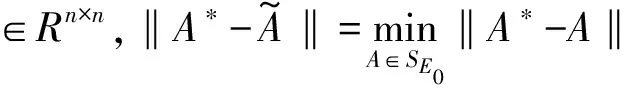
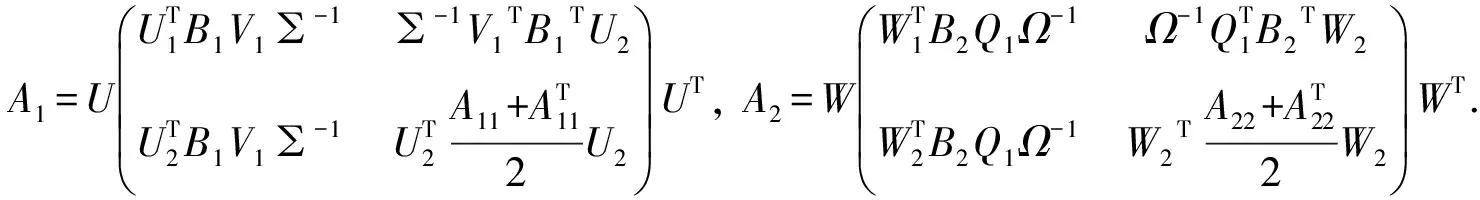
[1] 周树荃，戴华.代数特征值反问题[M].郑州：河南科学技术出版社,1991.

[2] 周富照,胡锡炎,张磊.对称正交反对称矩阵反问题[J].数学物理学报,2004,24A(5):543-550.

[3] Xie D X,Hu X Y，Sheng Y P.The solvability conditions for the inverse eigenproblems of symmetric and symmetric and generalized centro-symmetric matrices and their approximations[J].Linear algebra and its applications,2006,418:142-152.

[4] 谢冬秀,张忠志.对称广义中心对称矩阵模型修正的矩阵逼近法及其扰动性[J].计算数学,2008,30(3):247-254.

[5] 谢冬秀,刘仲云.线性流形上一类对称广义中心对称矩阵的最佳逼近问题[J].高等学校计算数学学报,2010，32(1):29-36.

[6] 谢冬秀,盛炎平.对称的广义中心对称矩阵逆特征值问题的最佳逼近[J].工程数学学报,2009，26(2):290-296.

[7] 孙继广.实对称矩阵的两类逆特征值问题[J].计算数学,1988,10(3):282-290.