基于壳向量的支持向量机渐进式增量学习算法

覃 俊，许 斐

(中南民族大学 计算机科学学院，武汉 430074)

支持向量机(SVM,Support Vector Machine)自Vapnik提出即成为机器学习和模式识别领域的研究热点，但其自身方法的复杂性成为处理较大规模数据时的瓶颈.在模式识别的实际应用中，很难在训练初期就收集得到一个完整的训练数据集，则希望机器学习的能力能随着训练过程中样本集的不断积累而逐步提高.因此，具有增量学习能力的信息分类技术，已渐渐成为信息智能化领域中的关键技术之一.

目前常用的、具有代表性的SVM增量学习算法有基于错误率最小的增量学习策略[1]、基于KKT(Karush-Kuhn-Tucker)条件的增量学习策略[2]等.但是，这2种方法并没有把部分普通样本包含进来，这部分样本尽管不属于支持向量集但距离最优分类面较近，可能转变为支持向量或不能被正确分类，但是直接舍弃不考虑，可能会导致分类精度下降.

本文在分析了这些代表性算法的基础上提出了一种基于壳向量的支持向量机渐进增量学习算法，该算法以求取壳向量来降低SVM训练过程中二次寻优的运算时间[3]，且更加完善了增量学习过程中的选择淘汰机制[4]，大大提高了SVM增量学习的训练速度；同时还利用由初始分类器确定的KKT条件来选择一部分增量样本进行训练，舍弃无用样本以减少其中噪点带来的干扰.二者结合构成了基于壳向量的SVM渐进增量学习算法能有效地提高增量学习的效率，尤其是在规模较大的样本数据集中，分类性能总体上优于其他算法.

1 壳向量

包含某一类训练样本集在内的最小凸集(特征空间中是一个多面体)称为训练集的凸壳，简称为凸壳.

壳向量(HV,Hull Vector)的思想[5,6]来自支持向量机中最优分类超平面的几何意义，即保证两类样本之间的最小间隔最大化，则支持向量一定只会在样本集合的最边缘位置上出现.如图1所示，A、B为分属两个不同类别的训练样本集，要使得二者最小间距最大化，支持向量是在图中标识的样本集的凸壳上产生，而不可能是凸壳内部的点.

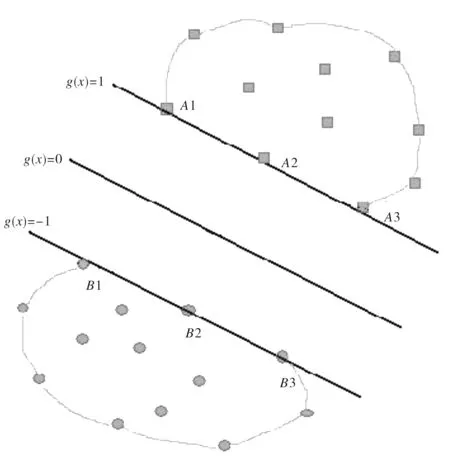
■表示训练集A的壳向量 ●表示训练集B的壳向量

1.1 支持向量与壳向量

图1中，{A1,A2,A3,B1,B2,B3}为支持向量，令H(A)表示对训练样本集A求壳向量集的算子，HVA则表示对应求得的壳向量集，S(A)表示对训练样本集A求支持向量集的算子，SVA则表示对应求得的支持向量，即HVA=H(A)，SVA=S(A)，可得出如下结论[5]：

1)SVA⊂HVA;

2)如果有A+表示A的同类增量样本集，且满足A∩A+=∅，则有：

S(SVA∪A+)≠S(A∪A+);

3)S(HVA∪A+)=S(A∪A+).

也就是说，壳向量集可以更好地表示原训练集中所包含的分类信息，因此与其它使用支持向量集代替原训练集的常用SVM增量学习策略相比，使用壳向量可大大提高训练速度.

1.2 壳向量的求解算法

1)初始化V0为包含给定训练集X在内的最小超球面上的点集，即V0={Sphere(X)}，且使V=∅；

2)对训练集X按照到超球中心的距离进行降序排列得：X*={SphereSort(X)}-V0；

3)whileX*≠∅ do,

有x∈X*，更新X*=X*-{x},

if (F(x,V)= = false)，则使V0=V0∪{x}；

4)whileV0≠∅ do,

取x∈V0；

if(F(x,V0-{x})= = false)，则使V=V∪{x}.

由上述步骤得到如图2所示的凸壳.

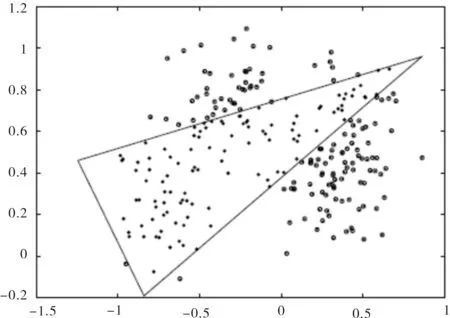
图2 基于超球面的凸壳示意图

2 支持向量机增量学习算法

2.1 算法思想

1)在增量学习之前，建立对初始样本有选择的淘汰机制[6].在初始样本集中选取一部分最有可能属于学习后所得支持向量集的样本集(即壳向量集)作为训练集，从而遗忘或丢弃对支持向量集没有影响的样本.再针对壳向量集进行SVM训练，求得支持向量集.

2)在利用先前得到的知识来对新增样本进行训练时，根据KKT条件，淘汰已被原分类器所识别的样本，保留违背KKT条件的新增样本，并上原壳向量集求取新的壳向量集并进行SVM训练，得到新的分类决策函数.重复上述步骤，即可连续对多批新增样本进行增量学习.

2.2 算法流程与算法描述

对于初始训练数据集A，可分为A+和A-两类待训练样本，每一类样本所对应的分类器和支持向量集分别为φA和SVA，增量学习的目的在于，在处理增量样本集B之后得到A∪B上的支持向量机φ和支持向量集SV.主要过程描述见图3.

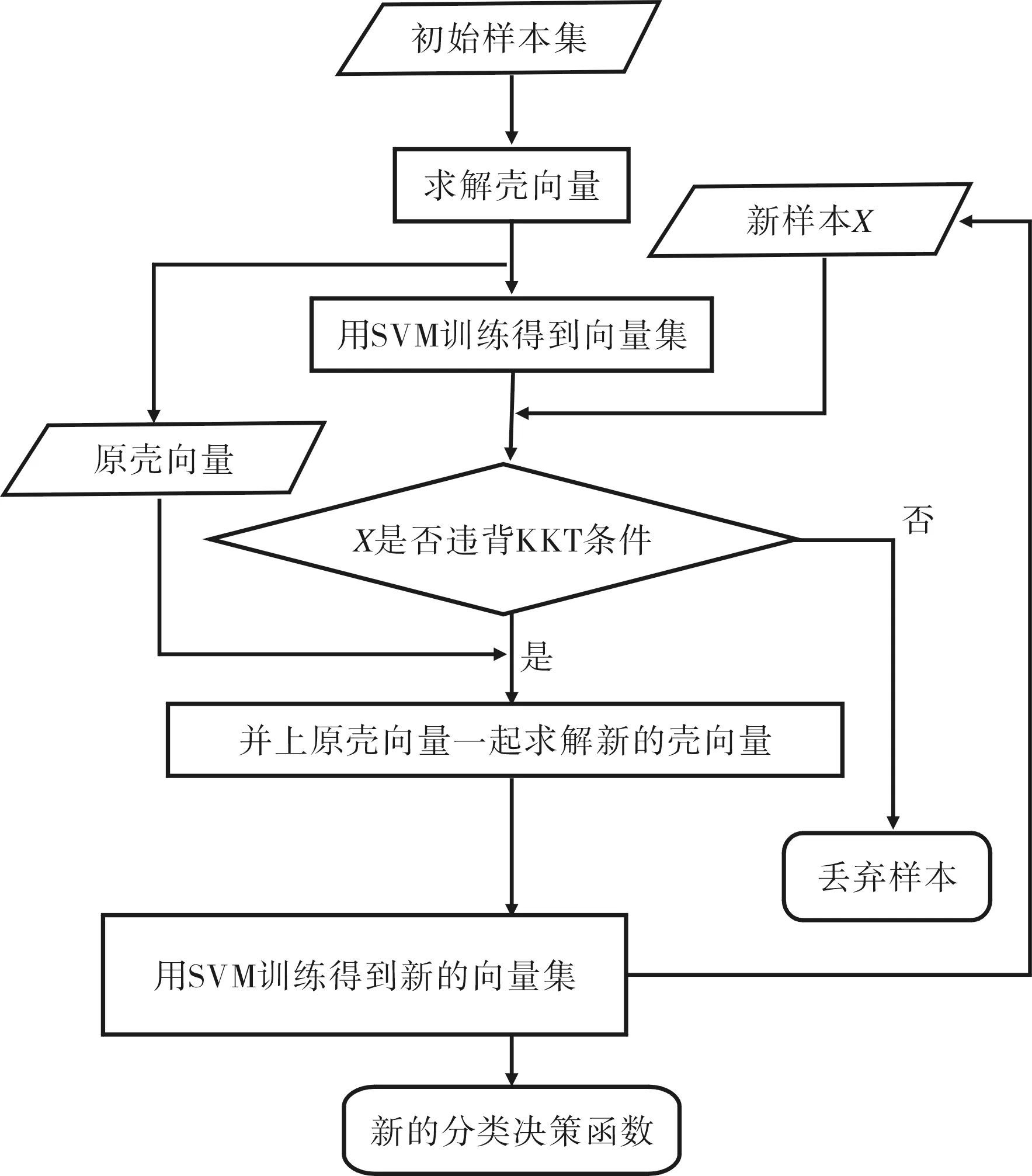
图3 增量学习流程图

算法描述及运行步骤如下：

(1)分别针对数据集A+和A-求壳向量集HVA+和HVA-，令HVA=HVA+∪HVA-；

(2)将(1)所求得的壳向量集HVA作为新的训练数据集，运用SVM算法得到一个分类器φA和对应的支持向量集SVA，以及由φA决定的KKT条件；

(3)构造工作集B′，B′为新增训练样本集B中所有违反φA定义的KKT条件的样本；

(4)如果B′=∅，则转至步骤(7)；

(5)如果B≠∅，则令HVA=HVA∪B′，作为新训练样本集，重新得到A+和A-，再针对A+和A-求新的壳向量集HVA=HVA+∪HVA-；

(6)返回步骤(2)，重复执行；

(7)输出更新后的φA和SVA；

(8)得到最终的支持向量机φ和支持向量集SV，算法结束.

3 数据仿真

为了验证该算法的有效性，这一部分将对实际数据进行仿真.其实验数据集Haberman来自UCI机器学习数据库，具体情况如表1所示.

表1 仿真所采用的样本数据集

仿真实验中支持向量机的训练是采用Matlab下的SVM工具箱，求取样本集的壳向量是采用Matlab下的Qhull工具箱(如图4所示).为了验证所提出的增量学习算法的有效性，本实验在Haberman数据集上，对4种不同的增量学习方法(算法)进行了比较分析，算法1为标准支持向量机算法，即每次增量学习都对全体样本求解分类器的方法；算法2是常用的以支持向量集(SVs)代替原始样本的方法进行增量学习；算法3是基于KKT条件的增量学习；算法4为本文所提出的基于壳向量和KKT条件的渐进式增量学习算法.

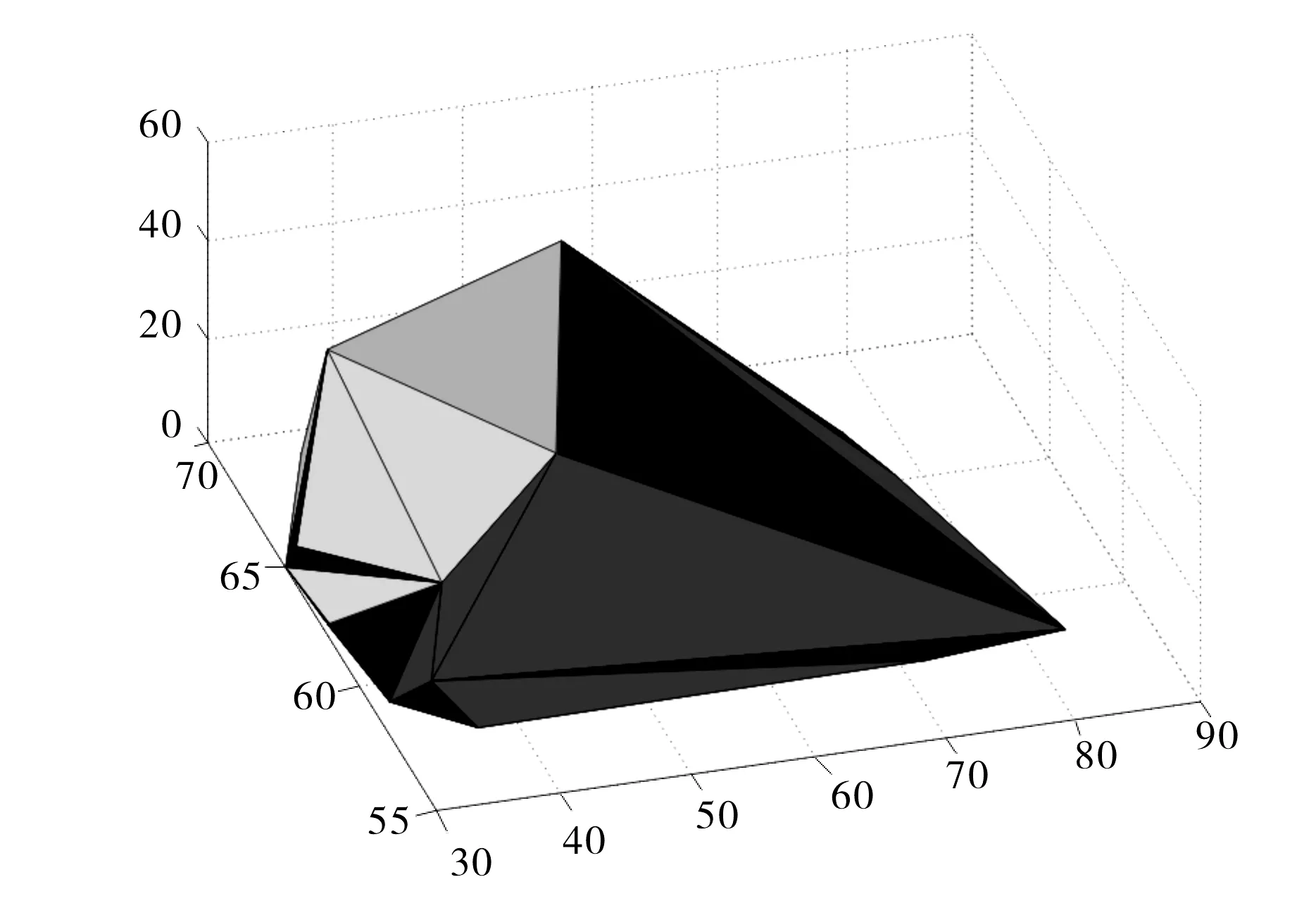
图4 对Haberman数据集所求得的凸包

先从数据集中随机抽取70%的样本作为初始样本集，然后分别进行3次增量学习，每次增加剩余样本的1/3，在增量学习完成后用全部样本来检验分类的效果.在Haberman数据集上的实验结果如表2～表5所示，SV表示支持向量，HV表示壳向量，t(s)表示训练时间，P表示训练精度.

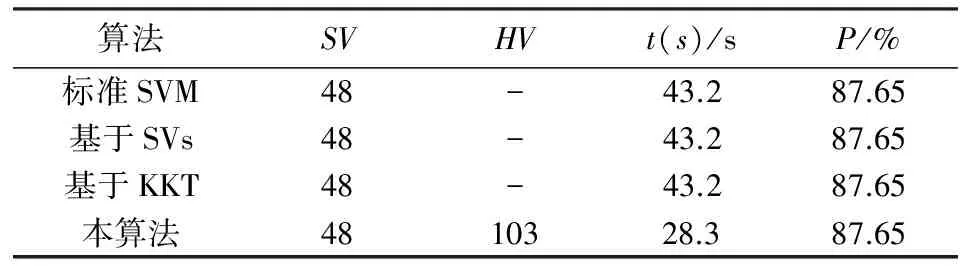
表2 初始学习的仿真结果

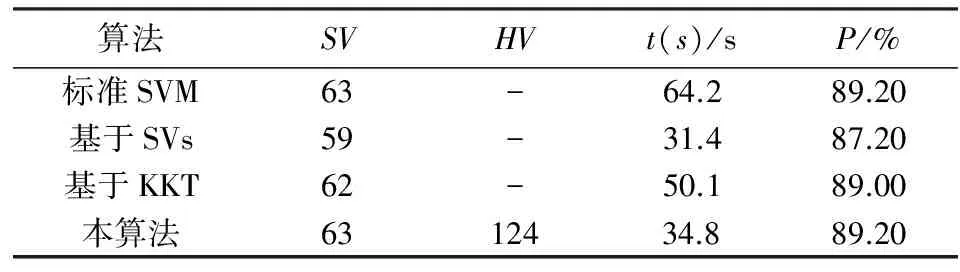
表3 第1次增量学习后的结果

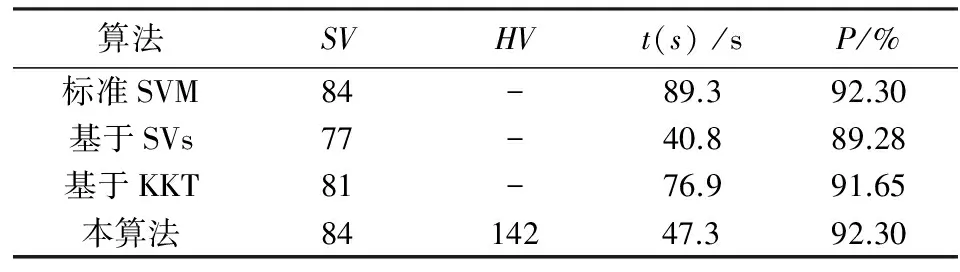
表4 第2次增量学习后的结果

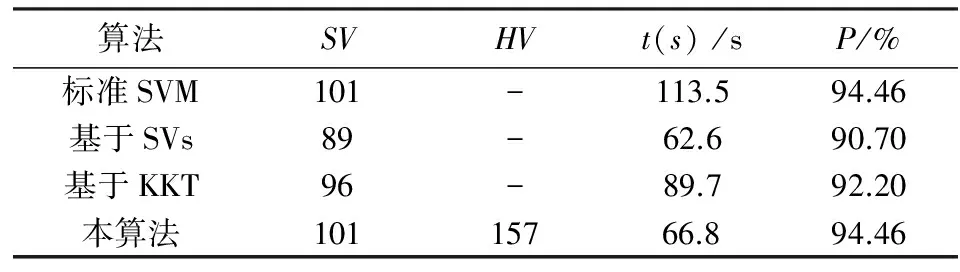
表5 第3次增量学习后的结果

从上述表和图的结果可以得出：基于支持向量的增量学习算法和本文所提出增量学习算法的训练时间差不多，甚至还略少一点，但训练精度低于本文所提出的增量学习算法；基于KKT条件的增量学习算法训练时间长，且在训练精度方面略低于本文所提出的增量学习算法.虽然算法3和本算法都利用了KKT条件来选取样本，但是本算法却没用KKT条件对初始样本集进行操作，而是利用几何意义上的壳向量集来代表原始训练集，这一策略使得待训练样本中包含了一些普通样本，还结合了经过KKT条件检验后的新增样本一起再进行训练，不仅保证了更高的分类精度，也提高了学习效率，所以本算法是可行有效的.

4 结语

本文在分析比较了几种具有代表性SVM增量学习算法的基础上，提出了一种基于壳向量的支持向量机渐进式增量学习算法，该算法在训练过程中对历史样本以及新增样本较好地实现了有选择性的遗忘淘汰机制，同时保证了良好的分类精度，最后通过仿真实验验证了算法的有效性.下一步的工作是将其扩展到手写体数字、少数民族文字识别等更广泛的实际应用中去.

[1] 萧 嵘，王继成，孙正兴，等.一种SVM增量学习算法a-ISVM[J].软件学报,2001,12(12): 1818-1824.

[2] 周伟达,张 莉,焦李成.支撑矢量机推广能力分析[J].电子学报，2001,29(5): 590-594.

[3] 李红莲，王春花，袁保宗，等.针对大规模训练集的支持向量机的学习策略[J].计算机学报,2004,27(5):715-719.

[4] Dong J X,Krzyzak A,Suen C Y.Fast SVM training algorithm with decomposition on very large data sets[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(4): 603-618.

[5] Osuna E,Castro O D.Convex hull in feature space for support vector machines[C]//Francisco J G.Proceedings of 8th lbero-American Conference on Artificial Intelligence.Madrid: Springer,2002: 411-419.

[6] 白冬婴，王晓丹，张宏达，等.对求壳向量算法的分析与实验[C]//李 映.第六届全国信号与信息处理联合学术会议.西安：陕西省信号处理学会，2007.