时变采样网络控制系统的容错控制器设计
樊金荣
(1中南民族大学 计算机科学学院,武汉 430074;2 华中科技大学 控制科学与工程系,武汉 430074)
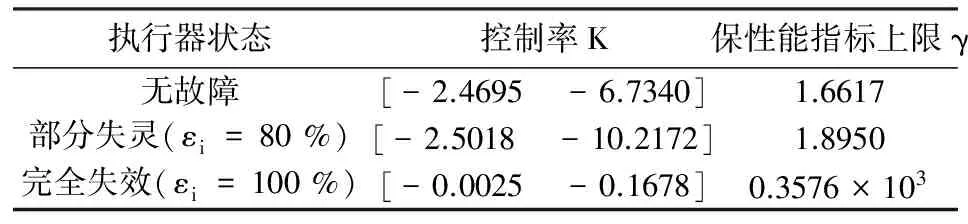
网络控制系统(NCS)的分析与设计大多是围绕网络时延而展开的,已经取得了不少的成果[1-4].研究网络控制系统中,通常假设传感器的采样周期为给定的常数.然而实际网络控制系统中,随计算机负载不同,器件故障及外部干扰等因素,采样周期会在某个标称值左右波动.近几年来,变采样周期的网络控制系统引起关注[5-13].文[5] 将采样周期表示为有限个元素的集合{c1,c2,…,cn},同时规定c1 另一方面,随着系统结构的复杂化,系统可靠性、安全性的要求也愈来愈高,网络控制系统的容错控制也引起了广泛的关注[3,4,12-15].文[3,4]构建了NCS时延模型,利用Lyapunov稳定性理论和容错思想,给出了系统参数不确定、执行器或传感器失效时保证系统鲁棒稳定的设计算法.文[12]针对存在外界扰动和参数不确定性的网络化系统,设计了执行器或传感器失效时具有鲁棒控制器并给出了鲁棒完整性的充分条件.文[13]分析了含扰动的情况下,网络化闭环故障系统具有鲁棒完整性的充分条件.这些控制器的设计中,仅考虑执行器或传感器正常或失效两种特殊情况.都是在输入矩阵与反馈增益矩阵之间引入开关矩阵L,使其对角线元素li=0表示正常,li=1表示失效.对应执行器或传感器部分失灵的情形没有考虑.同时考虑时变采样周期和容错控制,目前报道的成果仅在文[14]中,也是针对执行器正常与失效两种情形设计的. 本文针对网络控制系统在时变采样周期情形下,执行器从正常、部分失灵到失效这一连续变化过程的容错控制器设计问题,首先将时变采样网络控制系统离散化,将时变采样周期的不确定性转化成系统结构参数的不确定性,建立离散状态空间模型.在此基础上,利用Lyapunov稳定性理论和线性矩阵不等式方法,给出了执行器部分失灵或完全失效时,网络控制系统具有鲁棒稳定性的充分条件,设计了保性能鲁棒容错控制器.最后通过仿真实例,验证了所述方法的有效性. 符号说明:本文中MT表示矩阵M的转置.M>0意味着M为对称正定矩阵.‖M‖p表示矩阵M相对应的范数.“*”表示矩阵不等式中的对称项. 控制系统中,根据故障发生的不同部位,故障可以分成3类:传感器故障、执行器故障和系统元器件故障.当前伴随着现代工业制造技术的发展,传感器体积小,灵敏度高,进入微型传感器时代.这使得复杂控制系统中,大量传感器冗余硬件备份成为可能,这也是实现传感器容错控制一种简单易行的方法.执行器是控制行为实施的器件,完成传送必要的能量和功率去操纵被控变量的重要工作.由于这一特性,执行器通常体积大且质量重,如电磁阀等机构.在控制系统中对执行器采用冗余备份是不现实的.在过去的几十年中,执行器故障研究也是活跃的研究领域[14].系统元器件故障改变了系统结构参数和动态规律,很难检测与识别,一般不纳入容错控制的考虑范围中.为了简单起见,本文仅考虑单个执行器发生故障时的容错控制器设计. 考虑网络化控制系统,被控对象是一个线性时不变系统,可以用如下形式描述: (1) 其中,x(t)∈Rn,u(t)∈Rm,y(t)∈Rp,fa(t)∈Rm分别对应于系统的状态量、控制输出和感器输出及执行器故障.A,B,C是具有适当维数的已知矩阵. 目前对NCS的研究中,基本上都设定传感器为时钟驱动、控制器和执行器事件驱动的组合方式.不少的研究者从不同的方面阐述了事件驱动相比与时钟驱动的优越性[15].但对于多输入多输出(MIMO)的NCS而言,系统有多个传感器和执行器,它们在广泛的物理空间.若控制器采用事件驱动,将会导致控制器节点频繁访问网络,使网络中传送的令牌(Token)信号增加,占用大量的通讯带宽,从而加重网络时延和数据拥塞.另外,事件驱动相比时钟驱动比较难于实现,而且一些实际的控制网络不支持事件驱动.因此对这样的NCS,控制器采用时钟驱动是合理的选择.而执行器本质上是连续时间设备,控制信号一经到达,执行器立即响应,作用于物理对象上,其驱动方式为事件驱动才是最合理的[2]. 为了便于分析,凸现变采样周期网络控制系统容错控制的特点,本文作如下合理假设: (1)时变采样周期有界hk∈[hmin,hmax],h0表示网络控制系统采样周期标称值; (2)时延τk是时变有界的即τk∈[τmin,τmax],且只考虑短时延的情形,即hmax (3)系统中传感器和控制器为时间驱动,其采样周期hk=h0+τk,执行器采用事件驱动方式. 由于执行器端有零阶保持器,使得被控对象的控制输入量u(t-τk)在传感器在采样时刻tk同步改变,控制量在t∈[tk,tk+1]内保持不变且u(t)=u(tk). 对系统(1)以采样周期hk进行离散化,将时变采样周期的不确定性转化为系统结构参数的不确定性,得到如下离散控制系统: (2) 其中,Δk:=hk-h0表示采样周期的左右波动范围. [ΔAΔB]=DFk[E1E2]=DFk[AB]. 引理1 对于常数矩阵A,当t≥0时,恒有‖eAt‖≤eηt成立. 定理1 含有采样周期不确定项Fk是范数有界,τk∈[0,τmax],当实数β≠0且以下条件满足时,必有: (3) 证明当η≠0,由引理1有: 对离散控制系统(2),在执行器故障情形下,时变采样周期网络控制系统可以表示为如下形式: (4) 定义1 对系统(4),如果存在一个控制律u*(k)和一个正数J*,使得对所有允许的采样周期不确定性及执行器故障,闭环系统是渐近稳定的,且闭环性能指标值满足J≤J*,则称J*为系统(4)的一个性能上界. (5) 其中Q和R是给定的对称正定加权矩阵. xT(k)(Q+KTRK)x(k)<0, (6) 则u(k)=Kx(k)为系统(4)的一个具有性能矩阵P的二次鲁棒保性能控制律. 引理2 设Ψ是任意方阵,当且仅当存在矩阵X>0使得: (7) 成立时,则矩阵P=X-1使得ΨTPΨ-P+T<0. 引理3[17]给定适当维数矩阵Y,D和E,其中Y是对称的,则Y+DFE+ETFTDT<0对所有满足FTF≤I的矩阵F成立,当且仅当存在一个常数γ>0,使得Y+γDDT+γ-1ETE<0. (8) (9) (10) (11) (12) ΔV(x(k))=V(x(k+1))-V(x(k))< -xT(k)(Q+KTRK)x(k)<0, (13) 故系统是二次稳定的.由式(13)得到: xT(k)Qx(k)+uT(k)Ru(k)<-ΔV(x(k)). (14) 两边从k=0到k=∞求和,利用闭环系统(8)的渐近稳定性,可得: 下面证明定理的第2部分,由式(6),方程展开: xT(k)(Q+KTRK)x(k)<0⟹ (15) 由引理1,(15)式等价于存在对称矩阵X>0,使得: <0, (16) 定义矩阵: 式(16)可以改写为: (17) (18) 两次运用Schur补性质,再取M=KX,得到: <0. (19) 式(19)是线性的,当且仅当满足εi=0和εi=εimax两个极端情形时,才能保证所有εi∈[0,εimax]的情形满足. εi=0,表示执行器无故障正常运行;εi=εmax,表示执行器部分失灵最大故障,对应这两种情形,式(19)分别对应式(11)和式(12).证毕. 借用文[1]中的例子,NCS的被控对象表示为: (20) x0=[2 -1],假定采样周期标称值h0=1s,网络时延τ∈[0 0.05],假设式(5)定义的性能指标中,加权矩阵为Q=diag{5,2},R=0.5,设计一个鲁棒保性能容错控制器.运用MatlabLMI工具箱求解器mincx求解,得到闭环系统在执行器正常运行、部分失灵和完全失效时对应的控制率和保性能指标上限分别为如表1所示,可知系统在执行器故障下能找到相应的控制器保持闭环网络系统渐进稳定的. 表1 执行器故障时对应的控制率和性能指标 本文讨论了短时延网络控制系统中,系统的采样周期在标称值左右波动时,执行器部分失灵或完全失效情形下,闭环系统的渐进稳定问题.首先将采样周期的不确定转化为系统结构参数的不确定性,这样可以运用标准的鲁棒控制方法来处理采样周期的不确定性.接着提出了系统鲁棒保性能指标,给出通过求解LMI问题设计NCS容错控制器的设计方法.仿真实例显示,该方法可行. [1] Zhang W.Stability of networked control systems[D] .Ohio:Department of Electrical Engineering and Computer Science,Case Western Reserve University,2001. [2] Yang T C.Networked control system: A brief survey[J].IEEE Proceedings Control Theory and Applications.2006,153(4): 403-412. [3] Huo Zhihong ,Fang Huajing ,Yan Guihuan.Co-design for NCS robust fault-tolerant control[J].Transactions on Automatic Control,2004,49(2): 281-287. [4] Zheng Y.Fault diagnosis and fault tolerant control of networked control system [D].Wuhan: Huazhong University of Science and Technology,2003. [5] Gao Huijun,Wu Junli,Shi Peng.Robust sampled-dataH∞control with stochastic sampling [J].Automatica,2009,45(7):1729-1736. [6] Wang Yulong,Yang Guanghong.H∞controller design for networked control systems via active-varying sampling period method [J].Acta automation sinica,2008,34(7):814-818. [7] Sala A.Computer control under time-varying sampling period: an LMI gridding approach [J].Automatica,2005,41(12): 2077-2082. [8] Xie Guangming,Wang Long.Stabilization of NCSs with time-varying transmission period[C]// IEEE.IEEE International Conference on Systems,Man and Cybernetics.New Jersey:Institute of Electrical and Electronics Engineers Inc,2005:3759-3763. [9] Liu Fuchun,Yao Yu,He Fenghua,et al.Stability analysis of networked control systems with time-varying sampling periods[J].J Control Theory Appl,2008,6(1):22-25. [10] Yi J Q,Wang Q,Zhao DB,et al.BP neural network prediction-based variable-period sampling approach for networked control systems[J].Applied Mathematics and Computation,2007,185(2): 976-988. [11] Jung Eui-Heon,Lee Hong-Hee,Suh Young-Soo.LMI-based output feedback control of networked control systems [C]//IEEE.Proceedings of the IEEE International Workshop on Factory Communication Systems.New Jersey: Institute of Electrical and Electronics Engineers Inc,2004: 22-24. [12] 李 炜,张健全,李亚洁.基于NCS时延模型的鲁棒容错控制器[J].控制工程,2009,16(5):517-521. [13] Li W,Li Y J,Liu W R.Robust fault tolerant control for networked control systems with uncertain disturbance[C]//IEEE.Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation.New Jersey: Institute of Electrical and Electronics Engineers Inc,2007: 69-73 [14] Li Xuan,Wu Xiaobei.Guaranteed cost fault-tolerant controller design of networked control systems under variable-period sampling[J].Information Technology Journal,2009,8(4):537-543. [15] Ligusova J,Thiriet J M,Ligus J,et al.Effect of element initialization in synchronous networked control system to control quality [C]//IEEE.2004 Annual Symposium for Reliability and Maintainability.New Jersey: Institute of Electrical and Electronics Engineers Inc,2004: 135-140. [16] Boyd S,Ghaoui L E,Feron E,et al.Linear matrix inequalities in systems and control theory[M].Philadelphia: SIAM,1994. [17] 俞 立.鲁棒控制-线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.1 问题的提出与分析
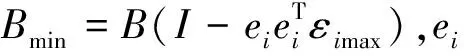
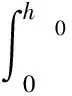
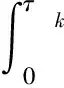
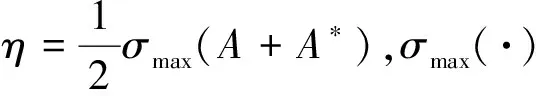
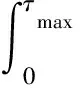

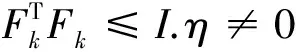
2 容错控制器设计

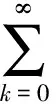
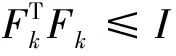
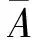
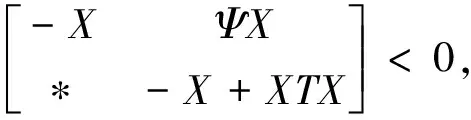


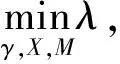
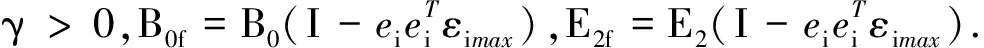

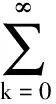
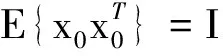
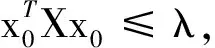
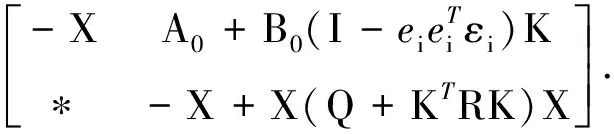
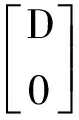

3 仿真实例
4 结语

