预应力下实验标定的盲孔法测试技术

孙 渊

（上海电机学院 机械学院，上海 200245）

预应力下实验标定的盲孔法测试技术

孙 渊

（上海电机学院 机械学院，上海 200245）

分析了盲孔法测量构件残余应力的理论基础，利用实验标定法确定材料在不同预应力下的应变释放系数A′和B′，并在理论释放系数A和B的基础上进行修正。施加预应力－400～400MPa后，通过盲孔法测量得到了应变值，并根据所得的A′和B′计算获得了残余应力。研究结果表明：A′和B′与应力水平有关，采用预应力下实验标定法进行盲孔法测试，计算所得残余应力值与实际的预应力值吻合程度较高，但它们之间有一定的误差，其相对偏差范围在2.2%～10.1%。研究结果可作为压入响应实验结果比较对象，促进压入响应下的残余应力测试应用研究。

预应力；应变释放系数；残余应力；标定实验

残余应力的存在对机械零部件的使用性能与寿命有着重要的影响，故残余应力测试技术一直是工程界关注的问题。目前，残余应力检测方法有多种［1］，其中以盲孔法为代表的有损检测法可靠性能高，测量精确，但是会对构件造成一定损伤，这在很多情况下是不可取的。压痕法是一种根据压痕弹塑性性能决定残余应力非常有潜力的方法，其具有简单和破坏性较小等特点。因此，研究压痕法测量残余应力，探索残余应力测试的实用技术具有重要的意义。在压痕法测量残余应力的实验研究中，一般采用盲孔法作为比较对象，分析和评估压痕法的测量精度和测量误差，故盲孔法的测量精度高、低就显得非常重要。因为盲孔法的测量精度与材料的应变释放系数A和B等因素有着很大关系［2-4］，所以A和B值的确定成为盲孔法研究的热点。近年来，为了提高释放系数的精度和效率，相关学者运用了有限元方法对材料释放系数进行研究［5-9］，分析释放系数的影响因素。文献［10］中指出应变释放系数A和B的绝对值随孔深与孔径比值λ的变化情况；文献［11］中指出盲孔孔径越小，钢管试件的释放系数A和B误差越小；文献［12］中引入模糊数学方法对应变释放系数进行评价，建立应变释放系数的模糊数学模型；文献［13－14］中研究材料发生屈服时释放系数的修正法；文献［15］中由标定试验得出多组应变释放系数值，并进行塑性修正，用于盲孔法测量SM400ZL钢焊接残余应力的工程实际中。

本文选择盲孔法作为研究对象，采用实验标定法确定材料在不同预应力下应变释放系数A′和B′，并用其来描述残余应力测量精度，分析其误差来源。

1 盲孔法测量原理

假设各向同性材料上某一区域内存在一般状态的残余应力场，其最大、最小残余应力分别为σ1和σ2。将专用应变花粘贴于该区域表面上，并在应变花中心钻孔。钻孔过程中，孔壁经历了弹性变形、塑性变形和切断过程，使得孔壁周围应力重新分布，引起孔边应力释放，从而在应变花丝栅区域内产生释放应变ε1，ε2和ε3，如图1所示。

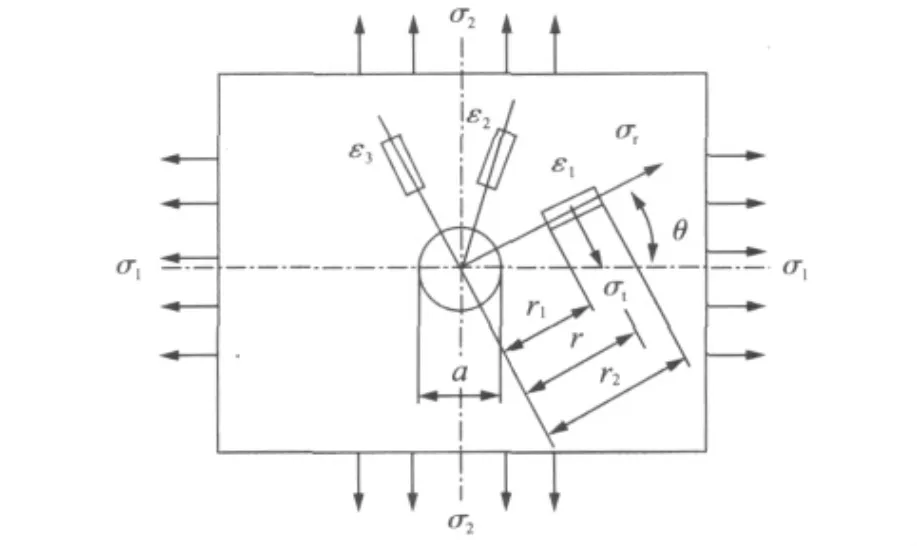
图1 盲孔法残余应力测量原理图Fig.1 Blind hole－drilling method for residual stress measurement

假定在与σ1成θ角的方向上，某点处周向和径向的残余应力为σt和σr，钻孔后该处重新分布的残余应力为σ″t和σ″r，因钻孔而在该处的释放应力为σ′t和σ′r，则

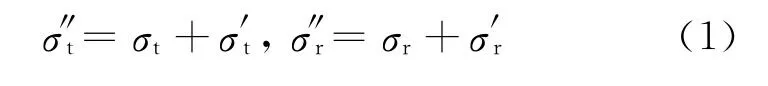
未钻孔前残余应力σt，σr和σ1，σ2有如下关系：

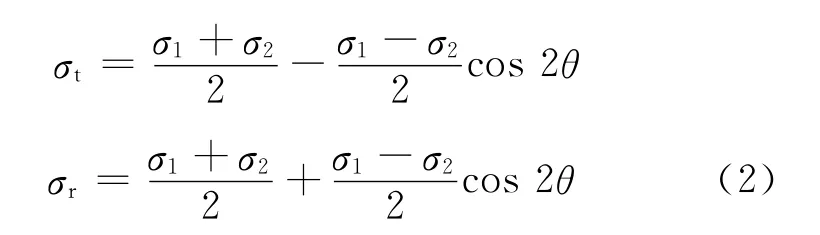
钻孔后σ″t，σ″r和σ1，σ2的关系，按 Kirsch的解，有

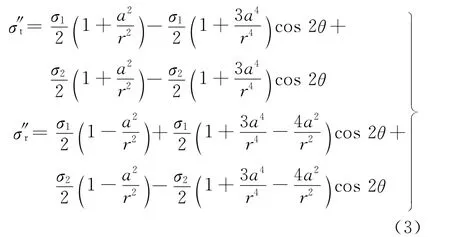
根据式（1）～（3）整理得因钻孔而释放的应力为

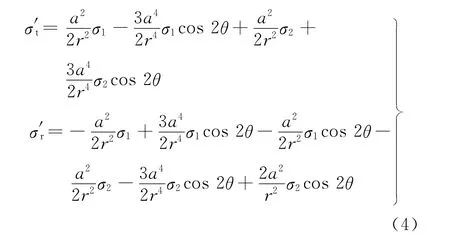
因此，只要测出释放应力σ′t和σ′r，就可求出残余应力σ1和σ2。

根据应力应变关系，该点释放应变εr与σ′t，σ′r的关系为

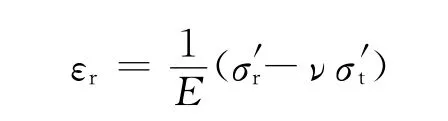
则εr与σ1，σ2的关系为

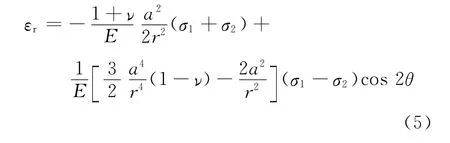
平均应变值为

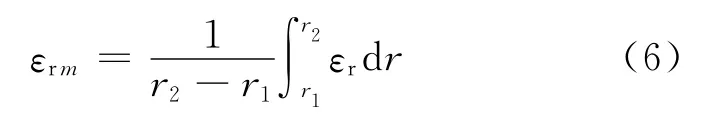
则有

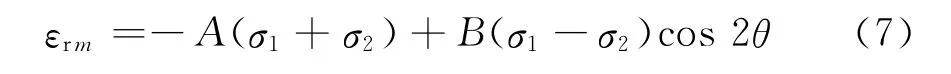
式中，

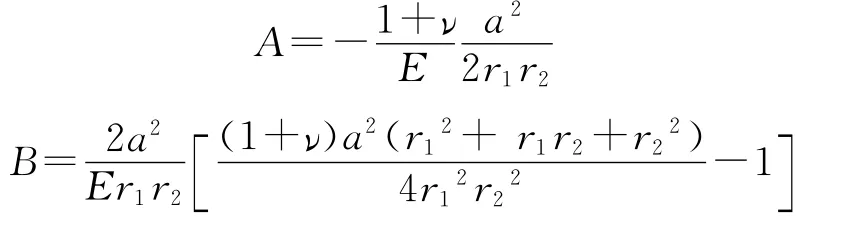
A和B为应变释放系数，它由材料弹性模量E、泊松比ν、孔径a、钻孔中心到应变片近孔端r1和远孔端距离r2等因素决定。当这些参数确定后，A和B为定值。实际上，每一种材料经过不同的热处理后，其力学性能变化很大，会存在微量残余应力，绝对无应力状态较少存在。其内部残余应力状况等因素会影响到A和B值，因此，用盲孔法测量残余应力时，确定A和B的值至关重要，它直接影响构件残余应力的测量精度。本文在理论分析基础上，主要利用实验标定法确定不同材料在预应力状态下的应变释放系数A′和B′，并用于残余应力测定的实验研究。

2 预应力状态下A′和B′的实验标定

本文利用实验标定法确定A′和B′，描述残余应力对无应力状态下A和B的影响程度。在此选用调质处理的试样材料40Cr和45号钢，它们的性能参数如表1所示，其中，σy为屈服强度，σb为抗拉强度。在试样的中间各粘贴2个残余应变花，其敏感栅尺寸为1mm×1mm，采用φ1.5mm钻头，转速为1 500r／min，钻孔深度h为2mm。为了简化，在构件中施加预应力，即单向应力场（σ1＝σ，σ2＝0），应变片1、3分别平行于σ1，σ2方向，即θ＝0，则在预应力下，

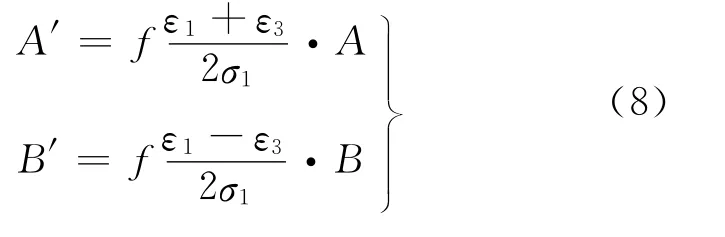
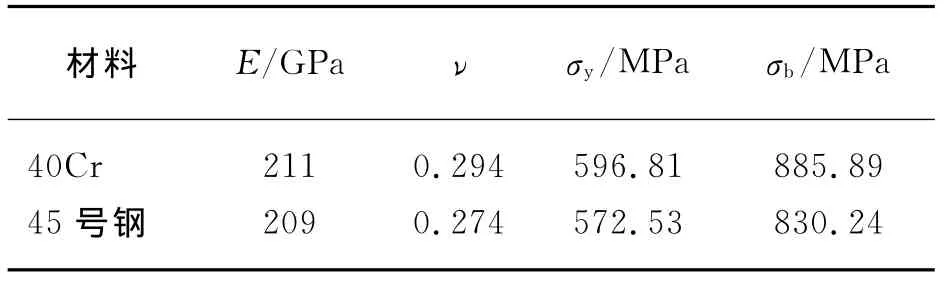
表1 40Cr和45号钢的性能参数Tab.1 The properties of 40Cr and 45steel

即由1、3应变片测得在预应力场中钻孔后的释放应变ε1和ε3，即可求出A′和B′，其实验测定结果如表2、3所示。

表2 40Cr的A′和B′实验测定值Tab.2 Measured values of release coefficients A′and B′for 40Cr

表3 45号钢的A′和B′实验测定值Tab.3 Measured values of release coefficients A′and B′for 45steel

从实验标定的结果看，A和B与构件中应力水平有关，在应力水平较低时，应变释放系数受应力水平影响较小，所以对于每一种材料应该在预应力状态下标定A′和B′。

由标定实验得出了在预应力状态下的多组应变释放系数值，并在理论标定的基础上进行孔边发生塑变后的应变释放系数修正。根据修正后的系数进行实验测试，从而提高测试精度，减少误差。

3 实验结果与分析

3.1 实验结果

本文选用专用残余应力钻孔装置（见图2）进行各种材料的残余应力分析和研究。该装置应力测量范围为－6～＋6GPa，分辨率为1με／字，所钻孔径为φ1.5mm，对中精度为25μm，打孔深度为2mm。型号XL2101B5的静态应变仪测量范围为－30～30 000με，应变片型号为BF120－1.5CF，电阻值为120±0.2Ω，灵敏系数为2.08±1%。

图2 残余应力钻孔装置Fig.2 Hole－drilling device for measuring residual stress

为了确保测量准确性，应严格按照其要求和规范进行操作，确定钻孔深度，钻孔速度及钻孔中心位置。同时，在试件中施加残余应力场（预应力），预应力的施加范围为－400～400MPa。为了简化，在构件中施加单向应力场（σ2＝0），钻孔结束稳定后测读应变仪数据ε1，ε2，ε3，根据预应力下实验标定法所得到的A′和B′，以及盲孔法计算公式为

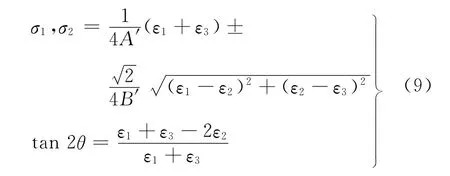
计算得出σ1，σ2，θ。

由于在试件中预先施加了残余应力场，所以就可以比较所测数据的正确性以及相应误差，如图3所示。图3中第1组材料为40Cr、第2组材料为45号钢，计算所得应力与实际所施加的预应力进行比较，吻合程度较高，但也存在一定的误差，其相对偏差范围为2.2%～10.1%。另外，在试件中施加了单向应力场σ1，即σ2的理论值为零，但通过测试应变量，计算得出σ2有较小的值。

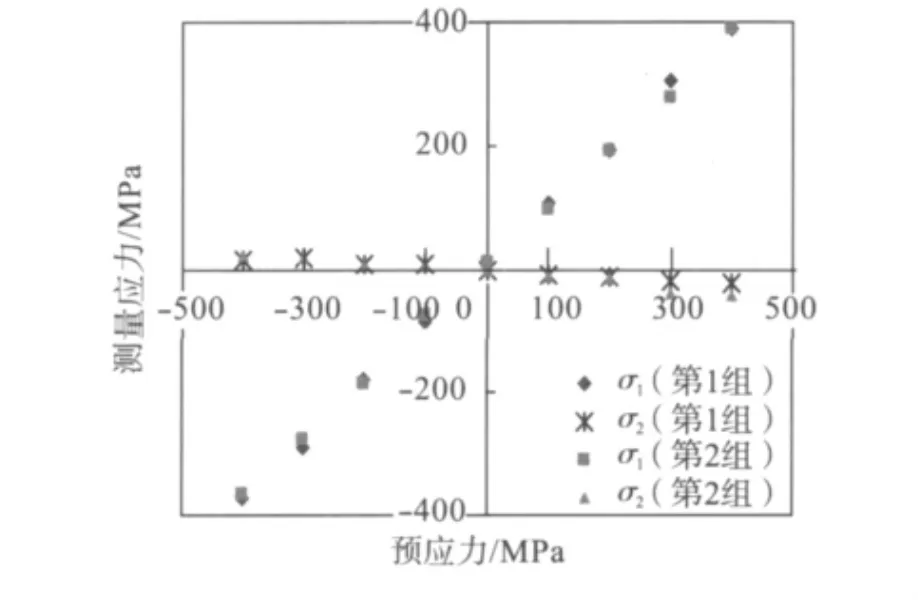
图3 两组材料所测应力值Fig.3 Measured stress of two groups of materials

3.2 结果分析

采用了实验标定法测得在不同预应力下释放系数A′和B′的值，在实际测量过程中，根据所测钻孔后释放应变数据ε1，ε2，ε3计算得到应力σ1，σ2，与实际构件所施加的预应力进行比较，它们之间有一定的误差，这些误差主要来自于如下因素：

（1）在实验标定法中，确定了在预应力状态下不同材料的释放系数A′和B′，标定时涉及一系列的操作误差，如应变片粘贴质量、仪器误差、操作误差等因素，会影响系数标定的正确性。

（2）在实际使用中，钻孔质量将直接影响残余应力的测定精度，故钻孔装置的准确定位和精湛的钻孔技术是测试的关键要素。另外，钻孔深度、钻具的磨损程度及钻孔速度同样会影响到测试精度，故每个环节都可能带来较大的误差，会降低测量精度。

（3）在实际问题中，任一物体都是空间结构体，它所受的力一般都是空间力系，故严格来讲任何一个实际的弹塑性力学问题都是空间问题，从而要归结为求解复杂的偏微分方程组的边值问题。但是，当研究对象的几何形状和受力情况在z向具有类似性时，可以经过适当的简化和力学的抽象处理，归结为所谓的x－y平面问题，使得分析和计算工作量大为减少。虽然这种做法能满足一般工程上的测试精度要求，但会引起一定的误差。本文中应变片的测量属于x－y平面在径向位置的测量，由此必然产生一定的误差，为了提高测试精度，将会进一步通过实验研究，利用系数加以修正。

4 结 论

（1）根据实验标定法，确定了在预应力状态下材料的释放系数A′和B′。通过实验研究可以发现A′和B′与构件中应力水平有关，但其影响程度较小。为了提高测量精度，有必要在预应力状态下标定材料应变释放系数A′和B′。

（2）由标定实验得出在预应力状态下多组应变释放系数值，并在理论确定释放系数A和B基础上进行了修正，得到较为合理的孔边发生塑变后的应变释放系数。

（3）通过盲孔法计算得到了构件残余应力，其与构件所施加的预应力有较高的吻合程度，但也存在一定的误差。因此，在测试手段、实验操作、A′和B′系数标定等方面还需进一步的研究。

（4）实际应用中，构件处于三维应力状态，而以平面问题简化处理引起的误差还需进一步的探讨并加以修正。

［1］Sun Yuan，Wang Qingming.Research status of residential stress measurement［J］.Journal of Shanghai Dianji University，2006，9（4）：6－10.

［2］Kabiri M.Toward more accurate resudual－stress measurement by the hole－drilling method：Analysis of relieved－strain coefficients［J］.Experimental Mechanics，1986，26（1）：14－21.

［3］王 政，刘 萍，高玉阳.A、B标定值对盲孔法测定焊接残余应力精度的影响［J］.甘肃工业大学学报，1987，13（3）：19－25.

［4］裴 怡，包亚峰，唐慕尧.盲孔法测定时计算公式中A、B值的研究［J］.机械强度，1997，19（1）：18－21.

［5］常 红，侯丽丽，杨自学.盲孔法测量复合材料残余应力释放应变矩阵的有限元分析［J］.太原科技大学学报，2006，27（2）：87－89.

［6］刘一华，贺赟晖，詹春晓，等.盲孔法中释放系数的数值计算方法［J］.机械强度，2008，30（1）：33－36.

［7］Bahadur A，Mitra A，Kumar B R，et al.Evaluation and correlation of residual stress measurement in steel［J］.Journal of Nondestructive Evaluation，2007，26（2／4）：47－55.

［8］Moharami R，Sattari－Fa I.Experimental and numerical study of measuring high welding residual stresses by using the blind－hole－drilling technique［J］.The Journal of Strain Analysis for Engineering Design，2008，43（3）：141－148.

［9］Beghini M，Bertini L，Santus C.A procedure for evaluating high residual stresses using the blind hole drilling method，including the effect of plasticity［J］.The Journal of Strain Analysis for Engneering Design，2010，45（4）：301－318.

［10］张晓宏，赵海燕，蔡志鹏，等.小孔法测量残余应力时孔边塑性应变的有限元分析及修正［J］.机械工程学报，2005，41（3）：193－200.

［11］王 龙.盲孔法测量圆钢管表面应力的试验与分析［J］.建筑科学，2009，25（9）：48－52.

［12］戴 晟，游 敏，陈 燕，等.盲孔法测定焊接残余应力应变释放系数的模糊数学分析［J］.机械强度，2007，29（5）：733－736.

［13］谭明鹤，王荣辉，黄永辉.盲孔法测残余应力中应变释放系数的修正方法［J］.热加工工艺，2007，36（19）：65－68.

［14］刘晓红，苏文桂，张运泉，等.屈服状态下盲孔法测量残余应力孔边应变释放系数修正［J］.铸造技术，2010，31（1）：36－39.

［15］张小鹏，王 娜.基于大型炉体焊接残余应力测试的盲孔法研究［J］.力学与实践，2007，29（3）：45－49.

Blind Hole－Drilling by Calibration Experiment under Pre－stress

SUN Yuan
（School of Mechanical，Shanghai Dianji University，Shanghai 200245，China）

The theoretical method of the blind hole－drilling method is analyzed for calculating residual stress.Strain releasing coefficients A′and B′of the materials under pre－stress are determined in a calibration experiment.They are revised based on Aand Bobtained with the theoretical formula.Strains around the blind hole are measured for materials in which pre－stresses ranged from－400MPa to＋400MPa.The residual stresses are obtained based on the strain releasing coefficients A′and B′.The results show that the strain releasing coefficients are related to the level of residual stresses.The residual stresses calculated fromA′and B′using the blind－hole－drilling method agree with the pre－stresses set purposely for the materials.Errors range from 2.2%to 10.1%.These results may be used as a reference in the study of residual stresses evaluation with the indentation method.

prestressed；strain release factor；residual stress；calibrating experiment

孙 渊（1969－），女，教授，博士，专业方向为机械工程，E－mail：suny＠sdju.edu.cn

TB 302.3；O 241.82

A

2095－0020（2011）03－0141－05

2011－03－28

上海市教育委员会科研创新项目资助（11YZ269）；上海市教育委员会重点学科资助（J51902）；上海电机学院科研启动经费项目资助（10C411）