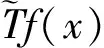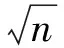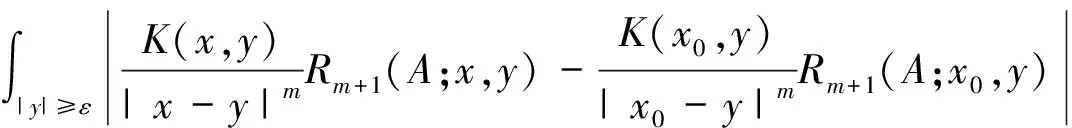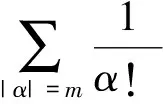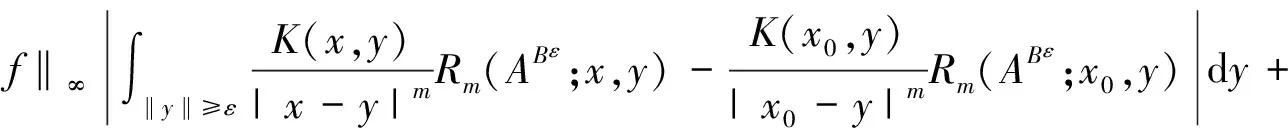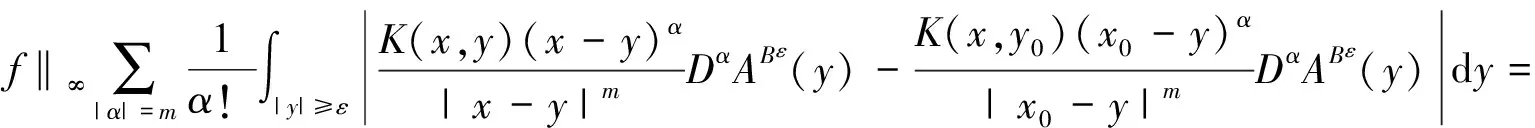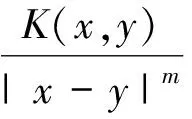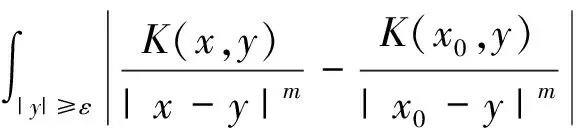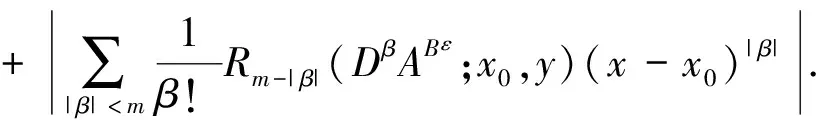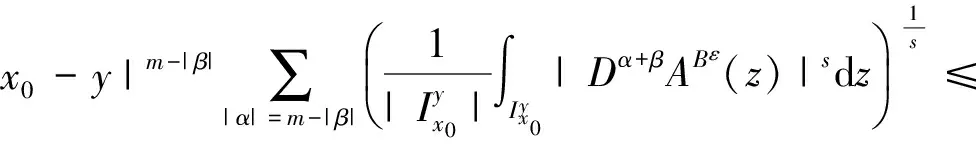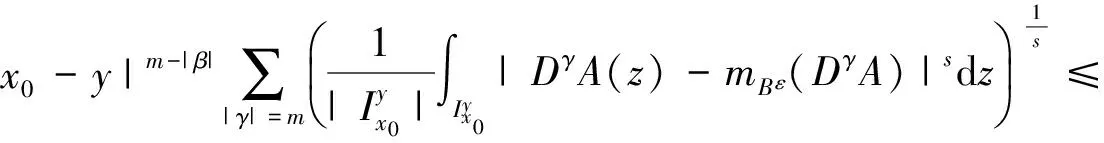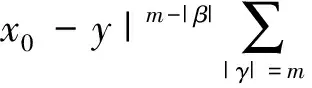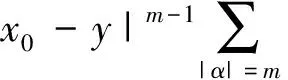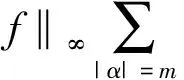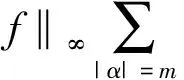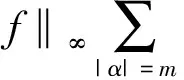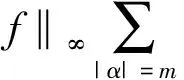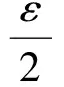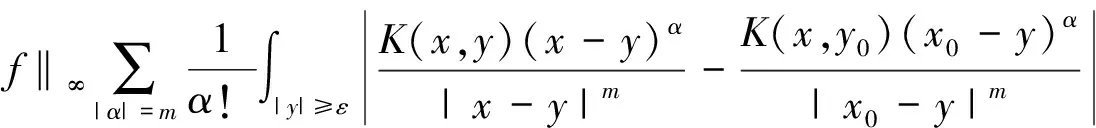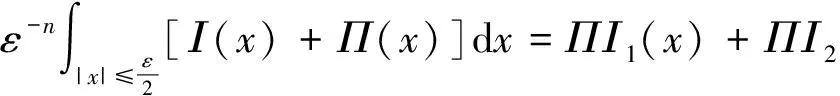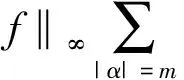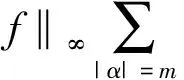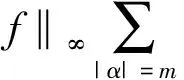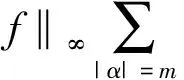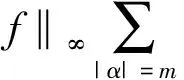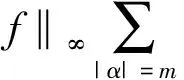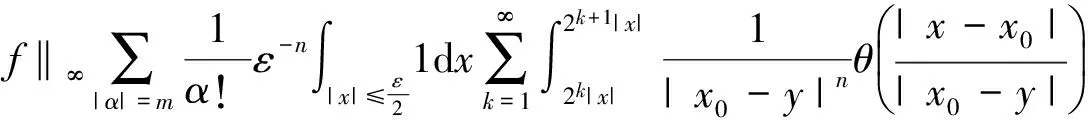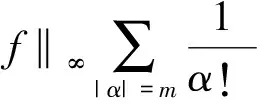推广的θ型C-Z核的多线性振荡奇异积分的型
张保俊,嵇 哲,李 华
(淮北师范大学 数学科学学院,安徽 淮北 235000)
0 引言
引言与预备知识交换子是一类与奇异积分算子相关联的重要算子,由于它与偏微分方程Cauchy积分等问题有密切的联系,所以交换子是调和分析的重要问题之一.而多线性奇异积分算子又是交换子的推广,因而具有重要的意义.θ型Calderon-Zygmund核是在1985年由Yabuta引入的,之后关于这一类带有θ型Calderon-Zygmund核的多线形奇异积分算子引起广泛的关注.
下面定义如下推广的θ型Calderon-Zygmund核:
定义1设θ为R+=(0,∞)上非负不减函数,若满足
1) |K(x,y)|≤C|x-y|-n,x≠y;
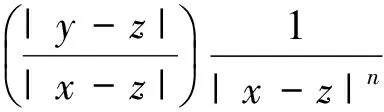

则Rn×Rn{(x,x):x∈Rn}上的可测函数K(x,y)被称为是一个推广的θ型核.


1 引理及主要证明
本文需要的几个引理.
引理1[3]设b(x)是定义在Rn上的函数,且m阶微商属于Ln(Rn),对某个s,n 则 引理5[5](Marcinkiewicz算子内插定理) 设T为线形算子.如果T为(p0,p0)(1 定理1的证明设f∈L1(Rn)∩L2(Rn),由引理2得, 其中M2f(0)≤‖f‖∞. 由于Rm+1(A,x,y)=Rm+1(ABε,x,y),所以 Ι(x)+Π(x). 由文献[3]知 |Rm(ABε;x,y)-Rm(ABε;x0,y)|≤ 由于|β| (*) 所以 同(*)方法 则 上面用到了关系式:|x0-y|≈|x-y|≈|y|≥|x-x0|. 同(*)方法 那么得到 Ι(x)≤Ι1(x)+Ι2(x)≤ 则 令 由于 则得到, 同理 由平移不变性,对任意球体B,存在ΙB,使下面不等式成立. 参考文献: [1]兰家诚. 具有θ型Caldreron-Zygmund核的多线形奇异积分算子的端点估计[J]. 数学进展,2006,35(6):712-720. [2]Lu S Z. Mulitilinear oscillatory integrals with Calderon-Zygmund kernel[J]. Science in China (Ser.A),1999,42(10): 1039-1049. [3]Cohen J,Gosselin J. A BMO estimate for multililinear singular integral[J]. Illinois J.Of Math,1985,30:445-464. [4]陆善镇,燕敦验. Calderon-Zygmund核的多线振荡形奇异积分算子的LP有界性[J].Science in China(Ser.A),2001,31(12):1087-1103. [5]丁勇. 现代分析基础[M].北京:北京师范大学出版社,2008.

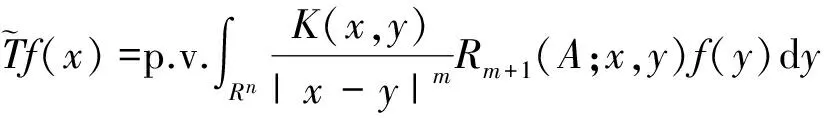
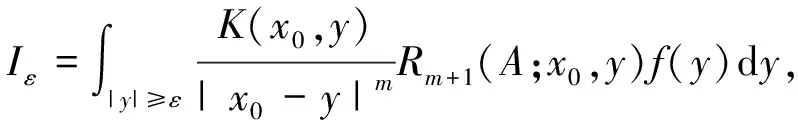



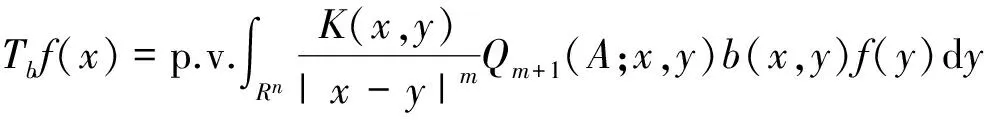
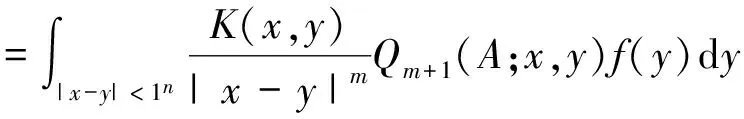
2 主要结果