Floyd算法在公交线路优化中的应用

王防修，周 康，同小军

(武汉工业学院数理科学系，湖北武汉430023)

Floyd算法在公交线路优化中的应用

王防修，周 康，同小军

(武汉工业学院数理科学系，湖北武汉430023)

以城市交通优化问题为例，研究了网络交通优化问题的数学模型。在已有Floyd算法的基础上提出了改进的Floyd算法，该算法能够有效地解决多权网络交通优化问题。以北京市公交为例，建立了多权交通网，讨论了从出发点A站到目的地B站的最优路线查询问题，运用Floyd算法建立该问题的数学模型。通过实例应用，进一步证明了该算法和模型的可行性和合理性。

最优线路;赋权有向图;Floyd算法;多权交通网;交通优化

随着社会的发展，最优线路问题成为研究交通问题中的一个重要问题，在解决公交最佳出行线路、城市援救最佳线路、物流配送、高速公路联网收费等与人们日常生活密切相关问题中发挥着重要的作用。这些年来，城市的交通系统有了很大发展，为公众的出行以及进行各项日常活动带来了很大的便利，但同时也面临着多条线路的选择问题。所以建立交通中最优线路问题的数学模型，为人们进行日常活动提供参考有很大的价值，是一个值得研究的课题。

建立交通中最优线路问题数学模型的目的就是寻找最优路径，为公众做出出行决策提供参考。目前关于最佳出行线路问题的研究主要是一些传统算法和根据问题的特点对传统算法进行改造。具有代表性的有 Dijkstra算法、Floyd算法、Bellman算法［1］;Angelica Lozano［2］研究了标号修正技术在综合运输网络中求解起点到终点的最短可行路径;Paola Modesti等［3］针对最小出行时间研究了求解综合运输网络最短路径问题，使用多标记图构建运输网络和对应的数据，并提出了求解算法。但这些已有的算法都不能解决出行线路双向选择、环形出行线路和多权问题，因此需要一种新的算法来建立交通中最优线路问题的数学模型。

1 最优线路的定义及评价指标

所谓最优线路是指从起始位置到目的地的最优行走路径或方案［4］。

最优线路的评价指标［5］有很多，其中主要有最短距离法、最短时间法以及某些特定要求(如沿途风景足够多等)。针对不同的人群及要求，所选择的评价指标包括如下几种。

1.1 最短路径

所谓最短路径是指在起始站点到目的地的所有可能线路中寻求距离最短的一条线路作为最优出行线路。

1.2 最少换乘车次

换乘车次是指乘客完成一次出行过程所需的换乘次数，次数的多少是衡量出行线路的最优与否的又一关键因素，若换乘次数较多，出行者会放弃对公交的选择，转向其他更快捷的方式。此外在同一票价的公交运营体制下，换乘次数的增加也意味着票价消费的增加，理想的出行线路应该保证在最少的换乘次数的前提下达到目的地。大量实际调研表明，最优出行换乘次数不应超过3次［6］。

1.3 最低票价消费

一般来说，乘客从起始站点到达目的地可选择的交通工具有多种，途径也不是唯一的，最低票价消费即要求满足保证乘客到达目的地条件下所有票价总和最小。

2 最优线路评价指标的量化

2.1 最短出行线路的量化

记Si为出行的起始点，Sj为所要到达的目的地，Dij表示从Si到Sj所有可能路线的距离，dij为从起始站Si到终点站Sj的第k条线路上相邻两站点的距离，则按照第k条线路行驶的总距离为：

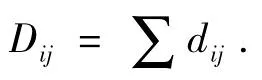
而最短路径即为所有可能行驶线路距离的最小值，即：

其中，k0为从Si到Sj所有可能线路中按最短距离所选的最优线路。

2.2 最少换乘次数的量化

对乘客而言，从起始点Si到目的地Sj可乘坐的主要交通工具是公汽，而公汽又包括一票制和分段计价两种不同方式。设从起始站Si到目的地Sj所有的可能线路有k条;用I、II表示乘坐单一票价、分段计价(1元票价、2元票价、3元票价)这两类公交;Ekj表示第k条线路上公交之间的转换次数;δi为标识函数，定义如下：

则从起始点Si到终点站Sj按第k条线路出行的换乘次数为：

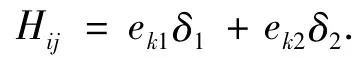
最少换乘次数为：

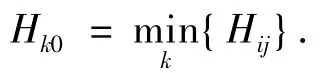
其中，k0为起始点Si到终点站Sj所有可能线路中按最少换乘次数所选的最优线路。

2.3 最低票价的量化

记Mij为从起始点Si到终点站Sj的票价消费，由于从起始点到终点站的可选择出行方式及线路有多种，如单一票价、分段计价，记cki为沿k号线路乘坐以上几种公交的次数，δi为标识函数(i=1，2，…，5)，且

则沿第k条线路出行的票价消费为：

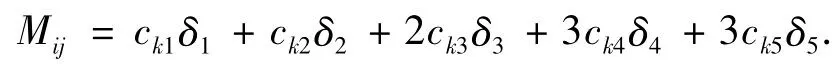
最低票价即为：

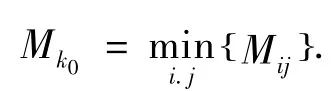
其中，k0为从起始点Si到终点站Sj的所有可能线路中按最少票价消费所选的最优线路。

3 Floyd算法

Floyd(弗洛伊德)算法［7-8］是一种矩阵(表格)迭代方法，对于求任意两点间的最短路、混合图的最短路、有负权图的最短路等一般网络问题来说均比较有效。

Floyd算法通过对表示有向图的邻接矩阵作叠代计算来解决有向图任意一对顶点之间的最短路径间题。Floyd算法不仅是建立在简单的数据结构基础之上，而且就解决问题的彻底性而言也是最完满的。迄今为止，它仅仅是作为解决有向图的最短路径问题的一个重要方法而被提及。实际上，Floyd算法与图的许多重要性质以及与图论中其它一些重要问题的解决有着密切的联系。

3.1 Floyd算法的基本原理

Floyd算法的主要思想是从代表任意2个顶点vi到vj的距离的带权邻接矩阵开始，每次插入一个顶点vk，然后将vi到vj间的已知最短路径与插入顶点vk作为中间顶点(一条路径中除始点和终点外的其他顶点)时可能产生的vi到vj路径距离比较，取较小值以得到新的距离矩阵。如此循环迭代下去，依次构造出 n个矩阵 D(1)，D(2)，……D(n)，当所有的顶点均作为任意2个顶点vi到vj中间顶点时得到的最后的带权邻接矩阵D(n)就反映了所有顶点对之间的最短距离信息，成为有n个顶点的图G的距离矩阵。最后对G中各行元素求和并比较大小，决定最优的路线。

3.2 Floyd算法构造距离矩阵的原理

对一个有n个顶点的图G，将顶点用n个整数(从1到n)进行编号［9］。把G的带权邻接矩阵W作为距离矩阵的初值，即从图的带权邻接矩阵W开始，递归地进行n次更新，即由矩阵D(0)=W，按一个公式构造出矩阵D(1);又用同样的公式由D(1)构造出矩阵D(2);……最后又用同样的公式由D(n－1)构造出矩阵D(n)。矩阵D(n)的i行j列元素便是i号顶点到j号顶点的最短路径长度，称D(n)为图的距离矩阵，同时还可以引入一个路由矩阵path来记录两点间的最短路径。

3.2.1 Floyd 算法步骤

d(i，j) ：d(k)ij.

path(i，j) ：对应于 d(k)ij的路径上i的后继点，最终的取值为i到j的最短路径上i的后继点。

Step1：赋权值，对所有 i，j，d(i，j)=a(i，j);当a(i，j)= μ时，path(i，j)=0 ，否则 path(i，j)=j;k=1。

Step2：更新 d(i，j) ，path(i，j) 对所有 i，j若d(i，k)+d(k，j) ≥ d(i，j) ，则转入 step3，否则 d(i，j)=d(i，k)+d(k，j)，path(i，j)=path(i，k)，k=k+1;继续执行step3。

Step3：重复step2直到k=n+1。

迭代结束后得到最终的距离矩阵D(n)和路由矩阵path，根据距离矩阵D(n)可得任意两点间的最短路长度，根据路由矩阵path可得任意两点间取最短路径。

3.2.2 回溯法求最短路径

已知路由矩阵P=(pij)n×n，利用回溯法求解点i与点j取最短路径，若已知pij=k1，分别从点i和点j开始回溯。

(a)从点i开始回溯

pik1=k2，pik2=k3，…，pikr=kr.

(b)从点j开始回溯

pk1j=q1，pq1j=q2，…，pqmj=j.

则从点 i到点 j的最短路径为：i，kr，kr－1，…，k2，k1，q1，q2，…，qm，j。

3.3 Floyd 算法改进

3.3.1 改进Floyd算法原理

在原有的Floyd算法中，矩阵D(k)给出网络中任意两点直接到达，经过一个、两个、……到(2k－1)个中间点时比较得到的最短距离。一般地在计算过程中，由于 D(k)其中从1到n取值。当n较大时，τ从1到n取值，比较之间的值取其最小，计算量大。

3.3.2 改进Floyd算法的计算步骤

4 Floyd算法实例应用

给出任意两公汽站点之间线路选择问题的一般数学模型与算法。并根据附录数据［18］，利用我们的模型与算法，求出以下6对起始站→终到站之间的最佳路线(要有清晰的评价说明)：S3359→S1828、S1557→S0481、S0971→S0485、S0008→S0073、S0148→S0485、S0087→S3676。

公汽换乘公汽平均耗时：5min(其中步行时间2 min)。

公汽票价：分为单一票价与分段计价两种，标记于线路后;其中分段计价的票价为：0—20站1元;21—40站2元;40站以上3元

该问题是一个多目标最优模型，可以根据对时间、转乘次数和车费的不同要求来选择最优线路。根据实际情况知，转车次数越多，所经过的站点数越多，相应的耗时也会越长，根据对乘客出行心里调查知，大多数乘客将转乘次数最少作为首要考虑因素，因此在本问题中求解出了转乘次数为一次和两次的情况，并记录每条线路所经过的总站点数，在根据不同的要求选择一条最优线路。

从表1可知，从S3359→S1828站中间换乘一次的乘车方式有9种，首先考虑费用最少，最少费用的乘车方案总共有8条，在该8条乘车线路中再考虑所经过的总站点数，选择一条最优线路。最优线路为：由S3359乘坐L469车次上行线路经29站到达S0304，再转乘 L167车次下行线路经 1站到达S1828，费用为3元，总共经过32站到达。其它线路依次类推。

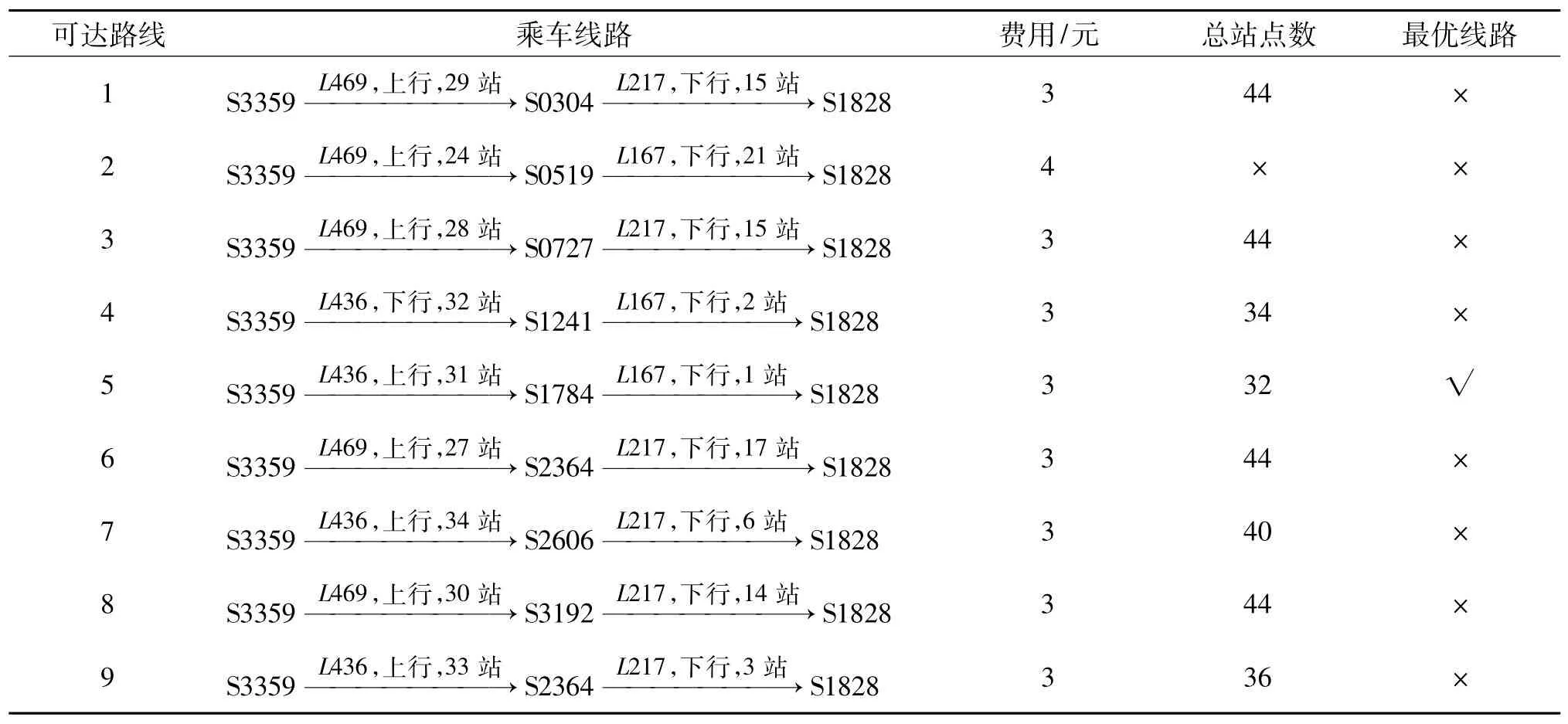
表1 S3359→S1828中转一站的乘车路线

从S1557→S0481站中间换乘两次的乘车方式总共有128种，表2中列出了其中的10种乘车方式，综合考虑乘车费用最少且经过的总站数少，从中选择一条最优线路。最优线路为：由S1557乘坐L084车次下行线路经12站到达 S1919，再转乘L189车次下行线路经3站到达S3186，再转乘L460车次环形线路经17站到达S0481，总费用为3元，总共经过32站到达。其它线路依次类推。

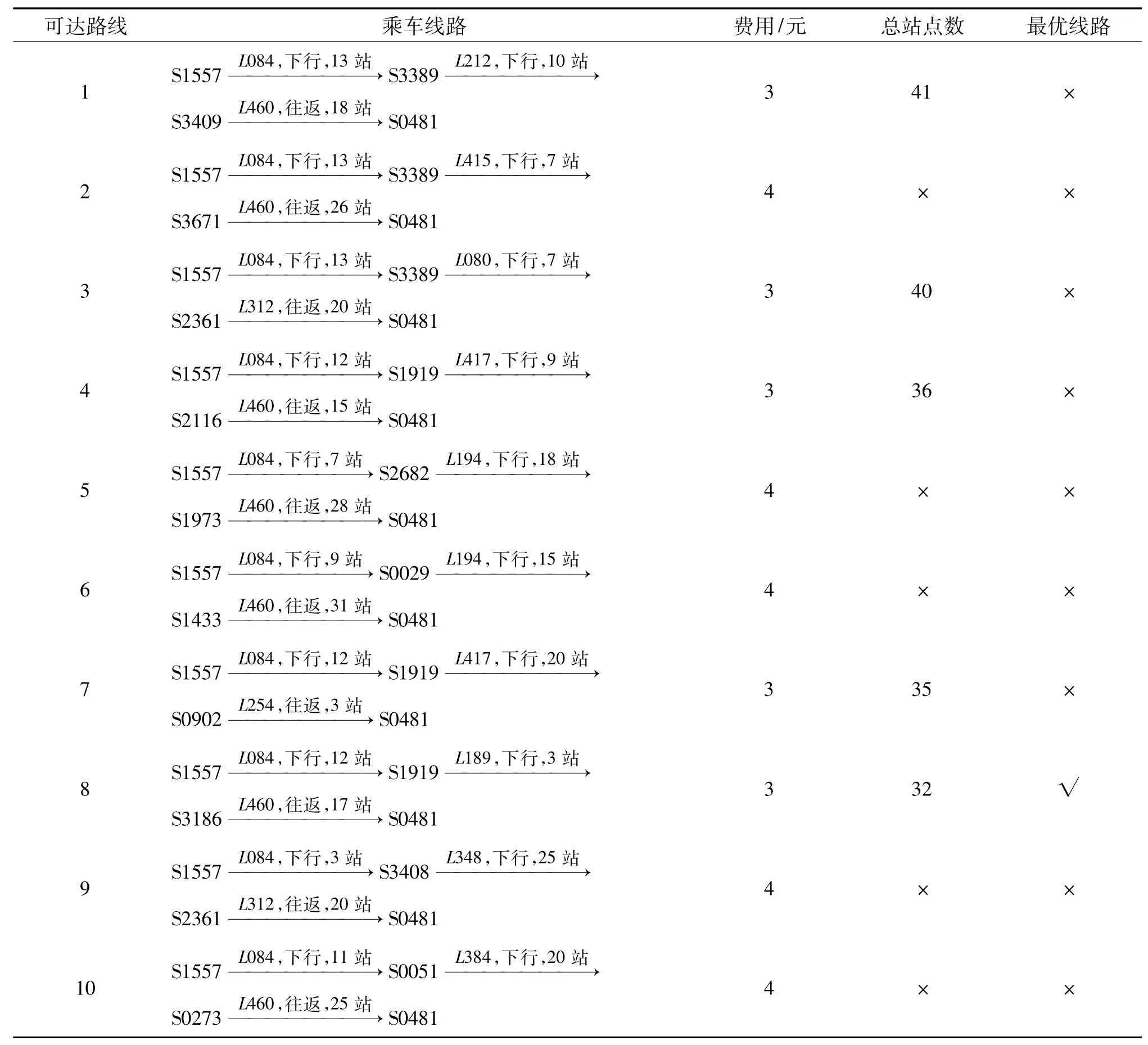
表2 S1557→S0481中转两站的乘车线路(部分路线)

5 结束语

本文主要利用Floyd算法解决一个实际问题。首先提出问题，在利用前面讲到的Floyd算法对提出的问题求解，做到了将理论应用于解决实际问题，为人们的方便出行带来参考。

［1］ 王杰.基于分层网络模型的单一讫(不同)点物流运送路径优化研究［D］.北京：北京交通大学，2002.

［2］ Angelica Lozano，Giovanni Storchi.Shortest viable path algorithm in multimodal networks［J］.Transportation Research.Part A 2001，35：225-241.

［3］ Paola Modesti，Anna Sciomachen.A utility measure for finding multimodal transportation networks［J］.European Journal of Operational Research.1998，111：495-508.

［4］ 许谷声，陈逸群，王解先，等.结合最优信息的路径搜索［J］.测绘工程，1998(4)：44-47.

［5］ 魏峰，夏小刚，张守刚，等.公交最优出行线路的一个模型及算法［J］.交通标准化，2008(6)：155-157.

［6］ 朱德通.最优化模型与实验［M］.上海：同济大学出版社，2003.

［7］ 米涅卡，李家滢，赵关旗.网络和图的最优化算法［M］.北京：中国铁道出版社，1984.

［8］ 钱项迪，运筹学［M］.北京：清华大学出版社，1990.

［9］ 赵静，但琦.数学建模与数学实验［M］.北京：高等教育出版社，2000.

Applying Floyd algorithm to optimize bus lines

WANG Fang-xiu，ZHOU Kang，TONG Xiao-jun
(Department of Mathematics and Physics，Wuhan Polytechnic University，Wuhan 430023，China)

Urban traffic optimization problem is put forward and the network traffic optimization mathematical model is studied.The paper proposes the improvement on Floyd algorithm.The algorithm can effectively solve the network traffic optimization problem.Finally，with Beijing traffic as an example，this paper sets up a multi－ weight traffic network.The optimal route is discussed from the point station A to the destination station B.At the same time，it establishs the mathematical model of the problem through Floyd algorithm.Further，it proves the feasibility and rationality of the model and the algorithm by an application example.

best routes;empowering directed graph;Floyd algorithm;multi－weight traffic network;traffic optimization

TP 301.6

A

1009-4881(2011)03-0037-06

10.3969/j.issn.1009-4881.2011.03.010

2011-01-13

王防修(1973－)，男，硕士，讲师，E －mail：wfx323@126.com.

国家自然科学基金资助项目(60574041).