竞赛图中的完美对集

高强

（山西大学 数学科学学院，山西 太原 030006）

竞赛图中的完美对集

高强

（山西大学 数学科学学院，山西 太原 030006）

Lichiardopol在离散数学-竞赛图中经过给定的0，1，2个公共顶点的圈一文中提出以下两个公开问题；对于阶为2n＋1的正则竞赛图T，（a）对任意的一个顶点w，是否存在n个有向三角形Ti生成T，且使得V（Ti）∩V（Tj）＝w（1≤i＜j≤n）是正确的.（b）是否存在一个顶点w，使得存在n个有向三角形Ti生成T，且使得V（Ti）∩V（Tj）＝w（1≤i＜j≤n）是正确的.文章扩充了满足条件的图类.

正则竞赛图；有向生成三角形集；完美对集

0 引言

设D＝（V，A）是有向图，V和A分别是有向图的顶点集和弧集，｜V（D）｜称为D的阶.对于任意的v∈V（D），用N＋（v），N-（v）分别代表v的外邻集和内邻集.定义d＋（v）＝｜N＋（v）｜，d-（v）＝｜N-（v）｜.设S⊆V（D），D 中由顶点集S 诱导生成的子图，记作D［S］.用N＋（v；D′）和 N-（v；D′），（N＋（v；W），N-（v；W））表示v在D′（D［W］）中的外邻集和内邻集.N＋（S；D′）和 N-（S；D′），（N＋（S；W），N-（S；W））表示顶点集S在D′（D［W］）中的外邻集和内邻集.

设有向图D，其中w∈V（D）.如果存在n个有向三角形Ti生成T，且V（Ti）∩V（Tj）＝w，（1≤i≤j≤n），那么我们说D有以w为公共顶点的有向生成三角形集.

设U，V是有向图D 的两个不相交的顶点集.称M是（U，V）间的对集，如果对任意的（u，v）∈M，满足u∈U，v∈V，M 记为（U，V）-对集.当｜U｜＋｜V｜＝V（D）且｜U｜＝｜V｜＝｜M｜时，称M 为（U，V）-完善对集.

完全图的定向图称为竞赛图.设T是竞赛图，对于任意的w∈V（T）如果满足d＋（w）＝d-（w），那么称T是正则的.显然可见，若T是阶为2n＋1的正则竞赛图，那么对于任意的w∈V（T）我们都有d＋（w）＝d-（w）＝n.

在本文中仅考虑几类正则竞赛图.

且文中所涉及的图论概念和记号，可参阅文献［1-2］.

1 预备工作

引理1 （Hall’s smarriagetheorem）［3］设G是具有二分类（U，V）的偶图，则G包含饱和U 每个顶点的对集，当且仅当，｜N（S）｜≥｜S｜对所有 Ø≠S⊆U，成立.

在有向图中应用引理1，可以立即得到下面推论.

推论1 设D是二部有向图，其两部顶点集分别为U，V，那么D具有（U，V）-完美对集当且仅当｜N＋（S）｜≥｜S｜对任意的Ø≠S⊆U 都成立.

引理2 设T是阶为2n＋1的竞赛图，其中w∈V（T），那么存在以w为公共顶点生成三角集的充要条件是存在（N＋（w），N-（w））-完美对集.

证明 设T是阶为2n＋1的竞赛图，其中w∈V（T），如果w是生成三角集｛Ti｝的公共顶点，那么弧集｛Ti＼w｝恰为（N＋（w），N-（w））-完美对集.反之，若 M 是（N＋（w），N-（w））-完美对集，由于T 是竞赛图，明显的顶点w和对集M 中的弧诱导出D中有一个以w为公共顶点的有向生成三角形集.

2 主要结果

定理1设T 是阶为2n＋1的正则竞赛图，w∈T 是一个顶点，U＝N＋（w）＝｛u1，u2，…，un｝，V＝N-（w）＝｛v1，v2，…，vn｝，若恰好存在一个整数m 满足

那么T中存在完美对集M.

证明设（S⊆U）是任意子集，m是任意一个正整数.

对于x∈S，有

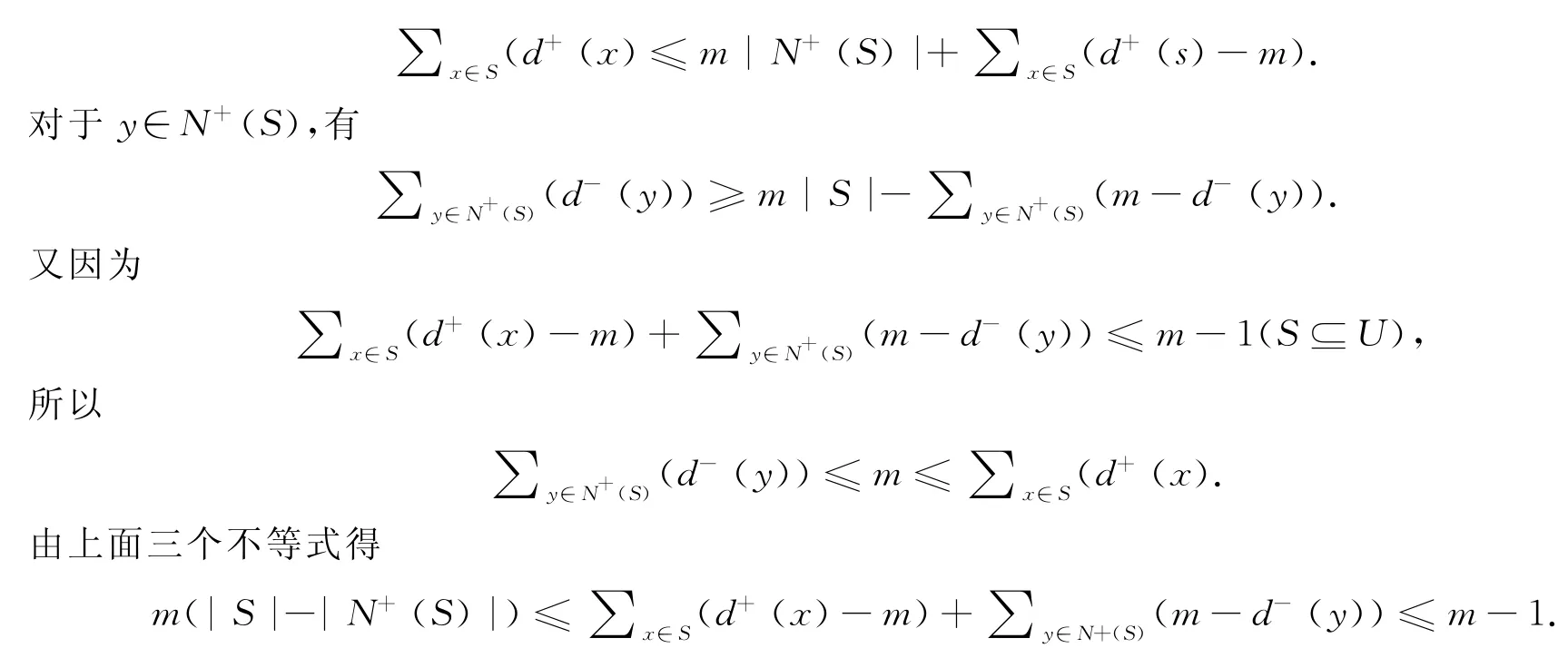
因为m 是正整数，所以｜N＋（S）｜≥｜S｜，

由于S是U任意子集，根据推论1，得T中存在完美对集M.

推论2设T 是阶为2n＋1的正则竞赛图，w∈T 是一个顶点，U＝N＋（w）＝｛u1，u2，…，un｝，V＝N-（w）＝｛v1，v2，…，vn｝，其中S是U 任意子集.若恰好存在一个整数m 满足

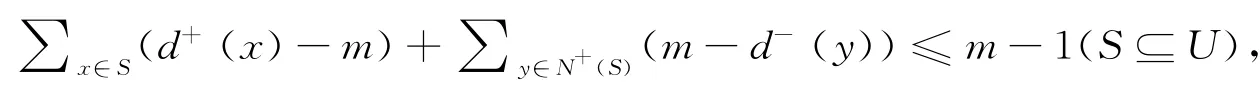
那么T中存在以w为公共顶点的有向生成三角形集.

在顶点集V（T′）∪｛u，v｝上定义正则竞赛图T如下：

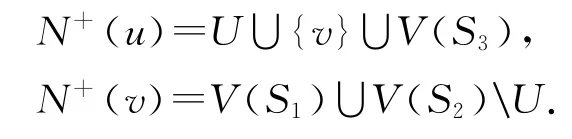
容易证明T是正则的.考虑顶点v的内邻集N＋（v）和外邻集N-（v）.顶点集｜V（S1）｜＝3但是N＋（V（S1，N-（v））＝U∪｛u｝，即｜N＋（V（S1，N-（v））｜＝2.则｜N＋（V（S1，N-（v））｜≤｜V（S1）｜.由于定理1知T中不存在（N＋（v），N-（v））-完美对集.由引理3知T中不存在以v为公共顶点的有向生成三角形集.但是利用定理1还可以验证当删除u，v时，新形成的竞赛图T′是正则竞赛图，而且对于任意的S是U的子集时，存在正整数m＝2，3，4，使得

所以T′存在完美对集M 而且存在以w为公共顶点的有向生成三角形集.

定理3设T是阶为2n＋1的正则竞赛图，w∈T 是一个顶点，U＝N＋（w）＝｛u1，u2，…，un｝，V＝N-（w）＝｛v1，v2，…，vn｝，其中S是U任意子集.若T同构于下面定义的集族Qn，则T中存在完美对集M的充要条件是T中存在以w为公共顶点的有向生成三角形集.

证明定义Qn集族是具有如下性质的正则竞赛图的图类：对于任意的Q∈Qn，存在一个顶点x∈Q，使.对于顶点ui控制顶点＝1，2，…，n），下标的获得通过mol（n）.根据定理1容易验证，对于每一对不同的整数i，j，ui，jj控制住的顶点可以不同，可以选择正整数m使得m＝n-2，满足

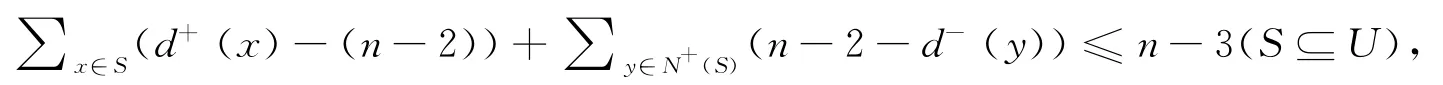
此时，Q中存在着完美对集M且Q中存在着以w为公共顶点的有向生成三角形集.

［1］ Bang-Jensen J，Gutin G.Digraphs［M］.New York：Springer，2002.

［2］ Chartrand G，Lesniak G.Graphs and Digraphs［M］.London：Chapman and Hall，1996.

［3］ Hall P.On Representatives of Subsets［J］.LondonMathSoc，1935，10：559-575.

［4］ Imrich W，Klavžar S.Product Graphs：Structure and Recognition［M］.New York：Wiley，2002.

［5］ Lichiardopol N.Cycles in a Tournament with Pairwise Zero，One or Tow Given Vertices in Common［J］.DiscreteMath，2008，308：763-771.

［6］ Lutz.Volkmann.Multipartite Tournaments：A Survey［J］.DiscreteMath，2008，307：3097-3129.

Perfect Matching in Tournaments and Dynamic Boundary

GAO Qiang
（SchoolofMathematicalSciences，ShanxiUniversity，Taiyuan030006，China）

Lichiardopol raised an open problems in his article“Cycles in a tournament with pairwise zero one or tow given vertices in common”，Discrete Math：For regular tournaments of order 2n＋1.（a）Is it true that for any vertexw，there existntrianglesTispanningTand such that：V（Ti）∩V（Tj）＝xfor 1≤i≤j≤n.（b）Is there a vertexwsuch that there existntrianglesTispanningTand such that：V（Ti）∩V（Tj）＝xfor 1≤i≤j≤n.In this paper，the results extend the conditions for the problems.

regular tournaments；spanning directed triangles；perfect matching

O157.5

A

0253-2395（2011）S2-0012-03

2011-08-11

高强（1987-），男，山东临沂人，硕士研究生，研究领域：图论及其应用.E-mail：luomu789＠126.com