基于模糊综合评判法的点权

郭 伟

（长治学院 数学系，山西 长治 046011）

基于模糊综合评判法的点权

郭 伟

（长治学院 数学系，山西 长治 046011）

文章主要研究了复杂网络中点权的计算方法。通过模糊综合评判法，给出了教学知识传播中教师的点权大小，对复杂网络中的点权计算进行了补充。

复杂网络；模糊综合评判法；点权

1 引言

近几年来，国内外掀起了研究复杂网络的热潮。对网络的研究最早起源于欧拉开创的图论。之后的近两百年中，数学家们一直致力于对简单的规则网络和随机网络进行抽象的数学研究。随着近年来计算机存储能力和数据处理能力的增强，人们获得了真实网络的特征数据，通过研究发现真实的网络既不是规则的，也不是随机的，而是呈现一定规律的复杂网络。复杂网络之所以复杂，不仅在于网络规模的巨大、网络结构的复杂，而且还在于网络在时间、空间上都具有动态复杂性，相应的网络行为也具有复杂性。实证研究发现：许多现实网络，包括信息网络、社会网络和生物网络都是复杂网络。本文主要研究的是复杂网络中的点权大小的计算。

所谓网络是由节点和连线组成的一个整体，这里的节点和连线是广义的，其中节点表示系统的组成元素，两节点的连线表示各元素之间的相互作用。虽然定义看似简单，但是网络却能够呈现高度的复杂性。网络的发展从最初的规则网络（度服从单点分布）到艾尔德和莱利的随机网络理论（度分布服从泊松分布）。然而，影响深远的进展则是近年来在统计物理中出现的小世界网络（smallworld networks）（度分布服从泊松分布）和无标度网络（scale-free networks）（度分布服从幂律分布）的研究。

泊松度分布如图1所示：图中的曲线是一条钟形曲线，该图形在网络平均度数k处有一个峰值。网络中大多数节点的连线都集中在它的附近，而连接线数远离它的结点所占比例指数衰减，说明具有泊松分布的网络节点有同质性，人们将k称为网络的特征标度（characteristic scale）。然而，另一个图中的曲线没有峰值，且随k衰减（如图2所示）。

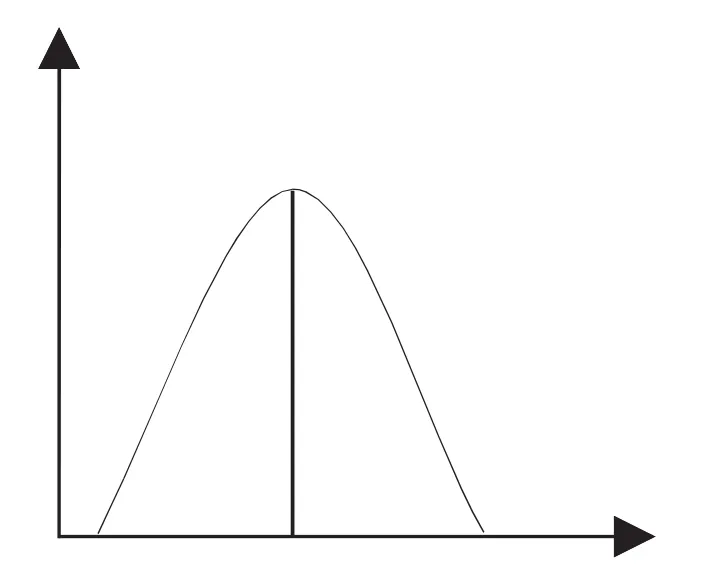
图2-1 泊松度分布

图2-2 幂律度分布

（其中横坐标表示节点数，纵坐标表示连线数）

从图形中还可以看出，现在大多数节点仅有少量连线，而少数节点拥有大量连线，这种节点称为中枢节点（hubs）。因为结点的异质性，于是特征标度消失了，为给这类网络一个名称，巴拉巴西（Barabasi）提出了无标度网络的概念。

无标度网络最重要的特性是标度不变性（scale invariance）。下面从指数函数与幂律函数对标度改变的反映来解释标度不变性或无标度特性的概念。

幂律函数y=cxa；指数函数z=ce-x。现在改变测量单位标度，即乘以因子λ，观察这两个函数如何变化。显然，

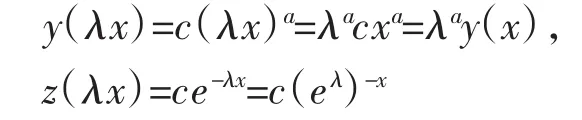
由第一个式子可知：函数图形的形状没有发生变化，同时函数的指数也没变。

由第二个式子可知：函数图形的形状已经改变，同时函数的指数也乘以因子。

以上说明幂律具有标度不变性，即不依赖于所采用的测量单位；而指数函数则不具备。

点权：在复杂网络中的加权网中，与节点度ki相对应的自然推广就是点强度或点权Si，其定义为：，其中Ni是节点i的近邻集合，ωij代表相邻两点间的边权。也就是说点权的大小由边权来决定。

2 主要方法和结果

上述复杂网络中对点权的定义，只是根据网络节点度的大小来衡量点的重要性。本文从真实的教学知识传播网络出发，以节点表示每个人，节点与节点之间的连线表示知识的传播。在这里节点与节点之间的不同即点权之间的差异主要是由每个人所拥有的知识量大小不同来决定的。当然，要精确地计算每个人的知识拥有量是不现实的，但是我们可以利用相对科学、合理的模糊方法来计算知识拥有量。因此本文利用模糊综合评判法来计算个人所拥有的知识量。

Istvan Z.Kissa等[1]在传染病模型的基础上研究了基于个体的有向加权网络模型，通过学科间的研究课题的扩散，说明了有向加权网络对知识传播的拟合性较好，并对有向加权网络中的权重进行了讨论。周涛等[2]对复杂网络上传播动力学研究做了综述，并介绍了经典传播模型，讨论了小世界网络和无标度网络的传播特性以及网络免疫技术，提出了实际传播网络的边的权重不同，如何去分析边权（或顶点权）分布对传播行为的影响的问题可研究性。以上文章都对网络中的点权的重要性进行了研究，但未给出其具体的计算方法。李鹏翔等[3]对原始的系统科学的研究方法通过度量节点删除时网络连通的破坏程度来反映网络节点（集）的重要性进行了改进，通过节点（集）被删除后形成的所有不连通节点对之间的距离（最短路）的倒数之和来反映节点删除时网络连通的破坏程度，即所删除节点（集）的重要性，从另一个角度考查了点权的重要性。以下是本文给出的具体方法。

由于确定一个人的知识拥有量并不能够精确的通过数据来计算，所以这里采用模糊综合评判法来求出教师的点权。在知识传播过程中，教师是知识传播的传播者。既然是传播者，那么发出信号是很关键的，即教师的语言表达能力是知识传播过程中的主要因素。以下通过对某班（49人）的调查研究运用模糊综合评判法求出点权，其中的指标体系参考考核教师教学工作的评价表得出。不同的是，这里采用了模糊综合评判法对教师的教学工作进行评测。

（1）确定因素集

（2）确定权重向量

评价项目的权重系数向量（如表1所示）

WF=（0.20，0.20，0.25，0.20，0.15）。

表1 某班教师测评

（3）统计、确定单因素评价隶属度向量，形成隶属度矩阵。该隶属度是表（1）中评价结果占总人数的比重。利用maple软件可得：

表1-2 某班教师点权

综合隶属度S=WFR=>

结果：可以看到，通过模糊综合评判法，可以更合理、更科学的计算出点权的确切数值，当然，在其他的网络结构中，点权的计算仍然可以通过此方法来计算获得。所以，本文是对复杂网络中的点权给出了又一角度的计算方法。

［1］Kiss，I.Z.，et al.Can epidemic models describe the diffusion of topics across disciplines？Journal of Informetrics（2009），doi：10.1016/j.joi.2009，（08）：002.

［2］周涛，傅忠谦，牛永伟.复杂网络上传播动力学研究综述［J］.自然科学进展.2005，15（5）：513-518.

［3］李鹏翔，任玉晴，席酉民.网络节点（集）重要性的一种度量指标［J］.系统工程.2004，22（4）：13-20.

Based on the Fuzzy Com prehensive Evaluation M ethod of Vertex W eight

GUOWei
（Departmentof Mathematics Changzhi University，Changzhi Shanxi 046011）

This papermainly studies a complex network vertex weight calculation method.By fuzzy comprehensive evaluation method is presented,the teachers'teaching knowledge dissemination of vertex weight of complex network size，the vertex weight computing added.

complex network；fuzzy comprehensive evaluation method；vertex weight

TP393

A

1673-2014（2011）02-0106-03

2011—01—06

郭 伟（1982— ），男，山西长治人，硕士，主要从事复杂网络研究。

（责任编辑 赵巨涛）