关于校正曲线建立和应用中一些问题的探讨

邓勃

(清华大学化学系,北京 100084)

关于校正曲线建立和应用中一些问题的探讨

邓勃

(清华大学化学系,北京 100084)

大多数仪器分析方法都是相对测量方法,需建立分析信号与分析物量值之间的相关关系,因此,正确建立和应用校正曲线是仪器分析中获得准确测定结果的基础。详细讨论了校正曲线的建立和标定方法,校正曲线的属性包括中心实验点的特性、校正曲线的精密度和置信区间、动态范围和线性范围的确定方法等。对校正曲线的应用中常遇到的一些实际问题如测定结果精密度的计算、标准偏差有效数字的确定、测定结果的表示方式等进行了讨论。

校正曲线;置信区间;线性范围;动态范围;有效数字

1 引言

分析检测是为科研和社会提供第一手原始数据和基础资料的有效手段。在科学研究中,它是做出科学推论和结论的基础;在经济活动中,它是评定产品质量、确定产品价格和发生国际贸易争端时进行仲裁的依据;在刑侦和司法活动中,它是做出公正结论的重要根据;在诊断疾病时,它是辅助医生正确判断疾病的必要资料,由此可见分析检测数据的价值和重要性。分析检测数据的重要性就在于它真实地反映了客观事物的属性,其价值取决于其可靠性,如果检测数据不可靠,就失去了它的使用价值,甚至会误导人们作出错误的结论。

在分析检测的实践活动中,最重要的是要采取一切措施保证所得到的数据和资料的可靠性。在仪器分析中,绝大多数分析方法都是相对测量方法,需要进行校正,建立分析信号与分析物量值(质量或浓度)之间的相关关系,即建立校正曲线。因此,正确建立和应用校正曲线是仪器分析获得准确定量分析结果的基本前提条件。

2 校正曲线的建立方法

建立校正曲线就相当于对平面上一组实验点取平均值,使校正曲线尽可能通过最多的实验点,且实验点均衡地分布在校正曲线的两侧,以达到实验点对校正曲线的偏差平方和最小。从数理统计的观点看,就是按照最小二乘原理建立分析信号y与分析物量值(质量或浓度)x之间的回归方程,确定校正曲线的斜率b和截距a[1-2]。

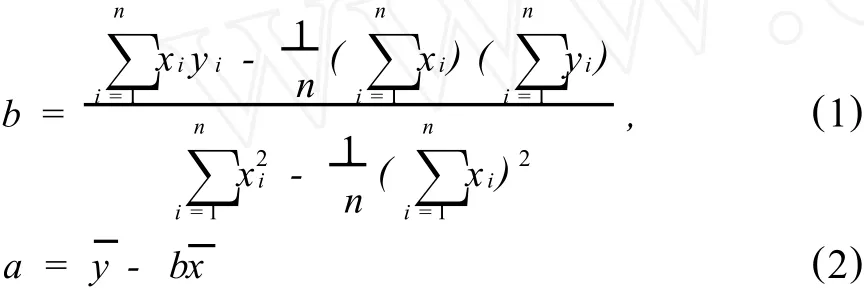
建立校正曲线应该采用多少个实验点比较合适,这是首先要考虑的问题。现在发表的文献中,通常都是用5个实验点,这是合适的选择。如果将分析物质量或浓度为零的‘空白’点参与回归,用6个实验点建立校正曲线更好。校正曲线的置信区间由±tα,fSE决定,其中SE是校正曲线的残余标准偏差,tα,f是显著性水平为α、自由度为f时的置信系数,可由统计书的t分布表中查得(见表1)。

tα,f值随f增大而减小,当f≥3后tα,f值随f增大而减小的速度减慢。tα,f值越大,tα,f SE越大,校正曲线的置信区间越宽,由校正曲线求得值的不确定程度越大。从控制校正曲线合适的置信区间考虑,f不要小于3,即实验点数目n不要少于5。试验点数目确定后,接着需要考虑实验点的分布。有人在酸性条件下,将味精中的硫化钠转化为硫化氢,用硫化钠检测试剂吸收后用紫外可见分光光度计测定,取硫化钠浓度分别是0、2.0、4.0、8.0和16.0μg的5个标准溶液系列建立校正曲线。按照校正曲线实验点精密度分布(见图1),校正曲线两端的实验点测量精密度差,特别是高端实验点变化大,对校正曲线的残余标准偏差贡献大,对校正曲线的稳定性有着显著的影响,当16.0μg实验点测定值偏高或偏低,将明显地引起校正曲线绕着中心实验点(¯x,¯y)发生转动。如果在校正曲线两端区域分别各有两个邻近试验点,按照测定值随机波动的特性,可有效地控制校正曲线的稳定性。由此可见,按上述方式依照浓度倍数布置实验点是很不可取的。实验点的合理分布应该是校正曲线中央布点可稀疏些,校正曲线两端区域实验点布置密一些,对于5个实验点,在校正曲线中央布一个实验点,在靠近低端、高端各布两个相互邻近的实验点。

表1 t分布表(α=0.05)Table 1 Values of t-distribution(α=0.05)

3 校正曲线的属性

3.1 中心实验点的特性

从式(1)可知,中心点(¯x,¯y)一定落在回归线上,位于校正曲线中间区域(在x=¯x附近)的实验点的精密度相对较好,对校正曲线稳定性的影响较小。因此,在测定样品时应尽量利用校正曲线的中央区域。

3.2 校正曲线的精密度

从标准溶液系列取样建立校正曲线,对特定的一次取样建立的校正曲线,斜率和截距是常数。由于分析信号y是随机变量,分析物的质量或浓度x是固定变量,y与x之间是相关关系,而非数学上严格的函数关系,每一实验点不一定都落在校正曲线Y=a+bx上。每一实验点分析信号yi偏离校正曲线期望值Yi的程度,可用偏差(yi-Yi)表示,所有实验点偏离校正曲线的程度,用校正曲线的残余标准偏差SE表式,

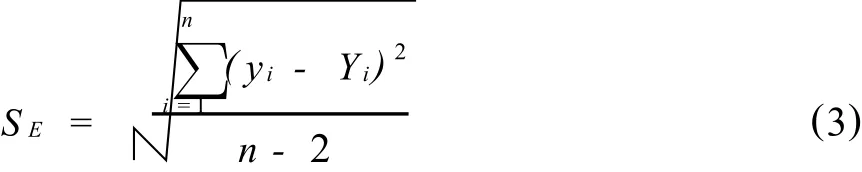
SE表征了校正曲线的变动性,直接影响到校正曲线的置信区间。

分析人员都知道,如果从同一标准溶液系列多次取样建立多条校正曲线,各条校正曲线并不都是重合的,也就是说各条校正曲线的斜率、截距未必都是相同的。斜率和截距的变动性分别用斜率、截距的标准偏差Sb、Sa表征,

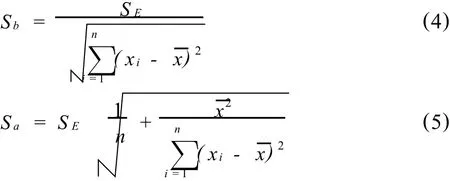
对于x=x0的分析信号y0的测定误差Sy0既受斜率b和截距a变动性的影响,又要受到测定时实验条件随机波动的影响。按照误差传递原理,测定分析信号y0的标准偏差

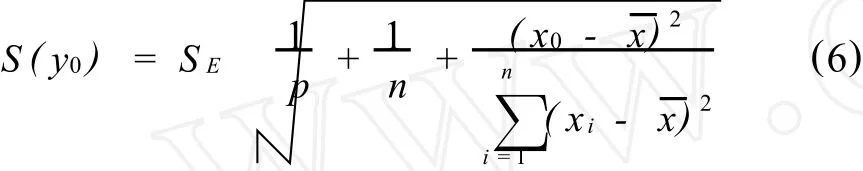
式中p是对x=x0的分析信号y0的重复测定次数,如果只进行单次测定,p=1。用图表示校正曲线各实验点精密度,如图1所示。

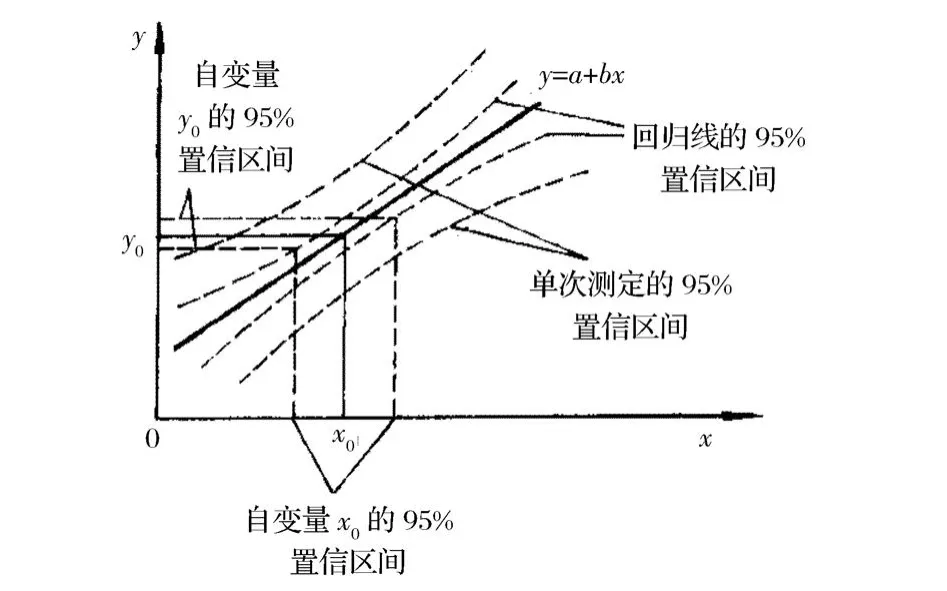
图1 校正曲线精密度分布曲线Figure 1.Distribution of precision values of a calibration curve.

式(6)和图1说明,①校正曲线中央的精密度优于校正曲线两端的精密度,测定值x0偏离中心试验点¯x越远,其分析信号值测定的精密度越差,因此,应尽量利用校正曲线的中央部分测定未知样品。②增加实验点数目n,有利于提高校正曲线的稳定性,因此,在总测定次数相同的情况下,适当增加实验点数目n减少实验点的重复测量次数是正确的选择,增加实验点的重复测量次数只能改善个别实验点的精密度,而增加实验点数目n则可提高校正曲线的整体稳定性;增加校正曲线低浓度和高浓度两端实验点的重复测量次数,提高它们的测定精密度,以改善整个校正曲线的稳定性。③将空白溶液实验点参与回归,增加实验点数目,有利于提高校正曲线的稳定性。④不用零浓度点的值扣‘空白’或调节仪器零点,用截距扣空白,因位于校正曲线两端的实验点测定精密度较差,用零浓度点的值扣‘空白’或调节仪器零点,就是用不稳定的值作为基准,会造成校正曲线的不合理平移。合理的做法是将零浓度实验点参与回归,用校正曲线的截距作为空白值,因截距值是综合了各实验点对校正曲线的影响而得到的值,稳定性较好,用它作为空白值,可提高空白扣除的准确性。

前面提到,校正曲线的变动是不可避免的。分析人员如何对校正曲线进行标定?现在有一种做法是采用单点标定,即用重新测定一个实验点的值对校正曲线进行标定。不管通过原点和新测定实验点的值来标定校正曲线(即斜率重置),或者是根据新测定实验点的值平移校正曲线,都是不甚合理的。斜率重置意味着只认可存在相对系统误差,而忽略了固定系统误差的存在;校正曲线平移意味着只认可存在固定系统误差,而忽略了相对系统误差的存在。事实上校正曲线通常既有平移又有转动,既存在固定系统误差又存在相对系统误差。可能有分析人员说单点标定不好,采用两个实验点标定可以吗?两点标定建立新校正曲线,通过原有的与新的校正曲线比较,虽然可以同时检查固定系统误差和相对系统误差,但仍是不可取的,其理由正如在第2节中指出的,用两点建立校正曲线是很不稳定的。值得推荐的办法是将原实验点和新标定实验点的值结合在一起重新建立校正曲线。

采用什么实验点进行标定,分析人员习惯用建立校正曲线的原质量或原浓度实验点重新标定校正曲线,如前述用紫外可见分光光度计测定味精中的硫化钠,用5个实验点中任意两个实验点,比方说用2.0和8.0μg标准溶液进行标定,当然是可以的,这相当于对此两个实验点又进行了一次或几次重复测定,改善了它们分析信号值的精密度。如果采用1.0和12.0μg标准溶液进行标定,效果又怎样呢?这相当于校正曲线新增加了两个实验点,能有效地改善新建校正曲线的稳定性,减小校正曲线的置信区间,提高了对两端实验点波动的控制能力。由此可见,用不同于建立校正曲线的原实验点进行标定,比用原实验点进行标定是更可取的。

3.3 动态范围和线性范围

按最小二乘原理建立的校正曲线一定是偏差平方和最小,但偏差平方和最小的校正曲线不一定是有意义的。建立的校正曲线是否有意义,用相关系数r进行相关性检验。校正曲线相关性检验如图2所示。

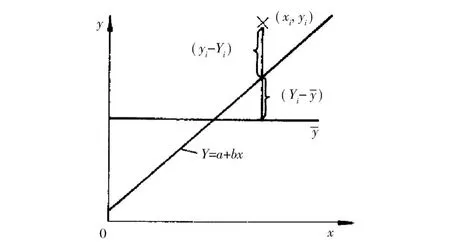
图2 校正曲线相关性检验示意图Figure 2.Illustration of the correlation test for a calibration curve.

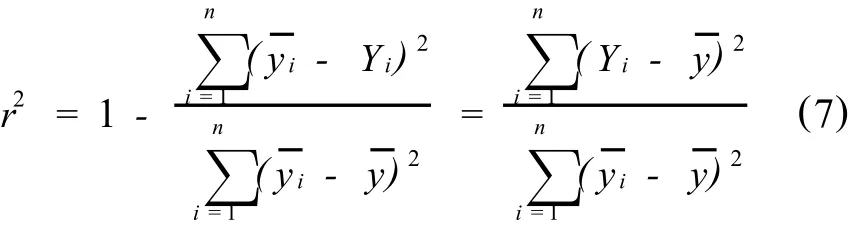
由式7可见,当y与x是严格的函数关系,所有实验点都落在校正曲线上,1;当y与x之间没有任何依赖关系时,各试验点的分析信号值不随分析物量值而变化,都为校正曲线是平行于x轴的水平线,==0。从实际分析观点考虑,斜率为零的校正曲线显然是没有任何实际意义,只有斜率足够大的校正曲线才有实用价值,从统计观点考虑,只有回归平方和够大,相关系数大于表2中一定显著性水平α和一定自由度f时的临界值rα,f时校正曲线才有统计和实用意义。通过相关性检验的校正曲线两端点之间所跨的分析物的量值范围,称为校正曲线的动态范围(dynamic range),在该范围内,分析信号y随测定量值x基本呈现线性变化,校正曲线两端区域可以有某种程度的弯曲。

表2 相关系数临界值Table 2 Critical values of the correlation coefficien ts

相关系数rα,f与显著性水平α与自由度f,亦即实验点数目n有关,当试验点数目为5(自由度为3),显著性水平α=0.05(置信度p=1-α=0.95),相关系数为0.878的校正曲线已有统计和使用意义,即使取置信度99%,相关系数为0.969也就够了。在一些文章甚至标准文件中,非要求相关系数达到0.999甚至0.9999,实在有点令人费解!应该指出,若不指明实验点的数目,只规定相关系数一定要达到几个9是不恰当的。

为什么通过相关性检验的校正曲线两端点之间所跨的分析物的量值范围,不能作为校正曲线的线性范围呢?因为实验点是否落在回归线上,除了实验误差之外,也包括了x对y的非线性影响。当对实验点进行了重复测定,将x对y的非线性影响与实验误差分辨开,用误差效应平方和Qe去检验失拟平方和Qd,可以确定实验点是否落在校正曲线上。失拟检验统计量

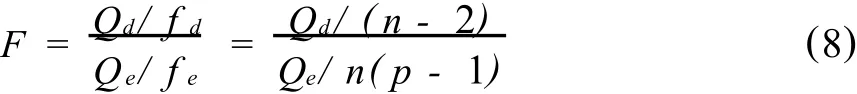
式中fd和fe分别是失拟平方和与误差效应平方和的自由度。当计算的F实验值大于F分布表中相应显著性水平α和自由度fd和fe的临界值,表明失拟情况显著,校正曲线已有明显弯曲。F分布表可由统计书中查到(见表3)。

通过拟合优度检验的校正曲线两端点之间所跨的分析物的量值范围,称为校正曲线的线性范围(linear range)。对实验点没有重复测量,不能得到Qe,就不能确定校正曲线的线性范围。

由上面的讨论知道,校正曲线的动态范围与线性范围是有区别的,不能混淆。动态范围一般大于线性范围,在有些情况下,动态范围与线性范围又是一致的。玆举一例予以进一步说明。在氯化十四烷基二甲基苄基铵存在下,于p H=6.5用铬天青S分光光度法测定钪,使用的标准溶液系列见表4[3]。

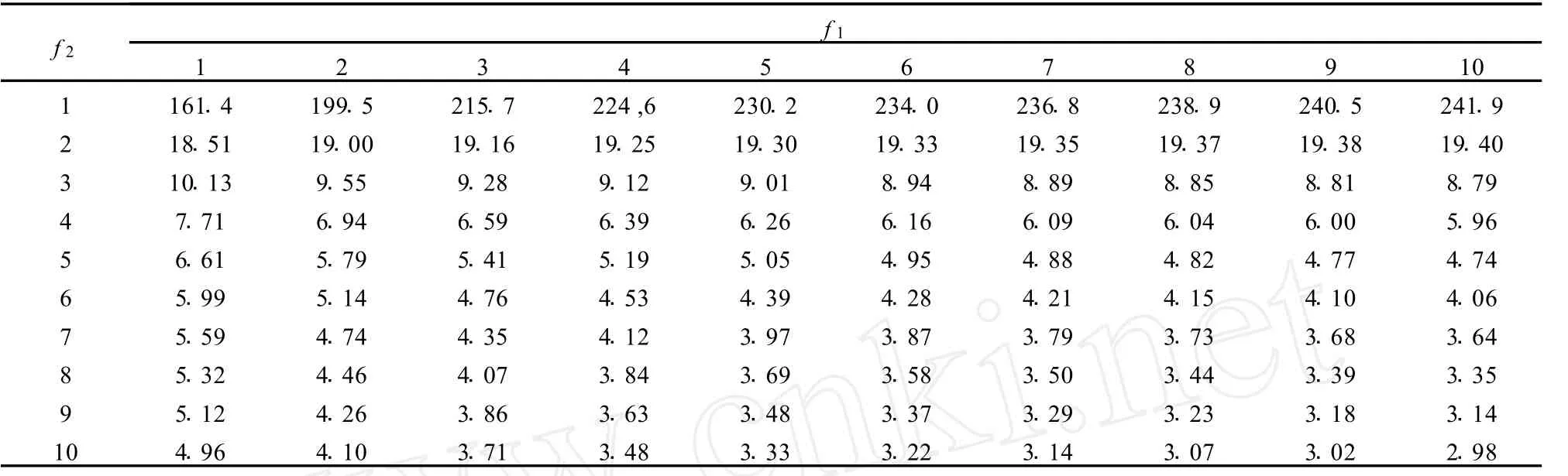
表3 F检验临界值表(单侧,α=0.05)Table 3 Critical values of the F-tests(single side,α=0.05)

表4 铬天青S分光光度法测定钪的标准溶液系列Table 4 A series of standard solutions for determ ination of scandium using chrome azurol S spectraphotometry

根据表4数据,拟合的校正曲线是y=0.145+1.103x,相关系数是r=0.9534,相关系数临界值分别是r0.05,16=0.468和r0.01,16=0.590,r大于r0.05,16和r0.01,16,表明所建立的校正曲线(图3的虚线)是有意义的,校正曲线的动态范围上限是0.48μg/mL。但从图3可以看到,当钪浓度大于0.16μg/mL后,校正曲线有明显的向浓度轴弯曲的趋势。由此说明,通过了相关系数检验的校正曲线所跨分析物量值区间内,实验点并非一定位于直线上,拟合优度检验的统计量值

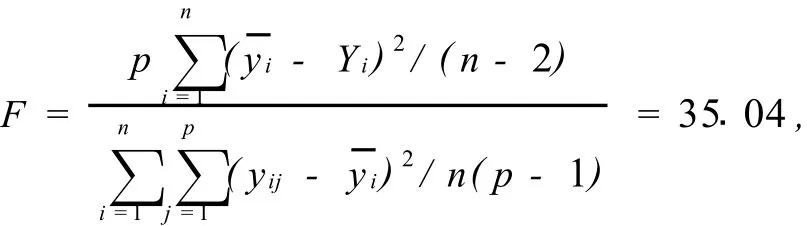
F＞F0.05(7,9)=3.29,失拟情况是高度显著的。如果舍弃0.16μg/mL后的实验点,由前面几个实验点建立校正曲线,y=0.09513+1.873x,相关系数是r=0.9977,拟合优度检验的统计量值

F＜F0.05(3,5)=5.41,校正曲线已不存在失拟情况。通过拟合优度检验的校正曲线(图3的实线)所跨分析物量值区间内,实验点都位于校正曲线直线上,校正曲线的线性范围上限是0.16μg/mL。校正曲线的动态范围远大于线性范围。

如果用表4中分析物浓度≤0.16μg/mL的几个实验点建立校正曲线,则动态范围与线性范围是一致的。

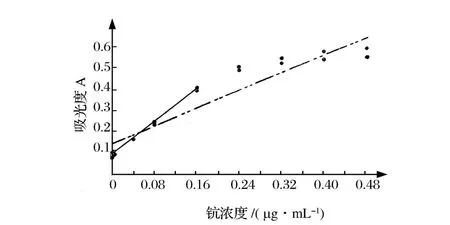
图3 校正曲线的动态范围与线性范围Figure 3.The dynam ic and linear range of the calibration curve.

3.4 线性范围不可外延性

校正曲线是对一组特定的实验点按最小二乘原理建立的,斜率和截距是常数,对不同实验点建立的校正曲线,其斜率和截距是不同的。校正曲线外延,就意味着肯定外延点也位于校正曲线上,事实上并不是这样,特别是高量值一端,校正曲线常常有向下弯的倾向,正如在图3中所看到,如果将校正曲线高端由0.16μg/mL延至0.24μg/mL,倾向开始弯曲,0.24μg/mL产生的失拟平方和将达到1.53× 10-3,而0.24μg/mL以前所有各实验点产生失拟平方和也只有2.91×10-4,可见任意外延校正曲线有可能造成校正曲线的严重失拟。校正曲线在低量值端,有时也出现向上弯曲的倾向,向下端外延也会造成校正曲线失拟。如果从专业知识或经验上确知外延点仍在线性范围内,外延也是允许的。但最好是用外延点进行实验,予以证实。

现在还有不少文献中,建立校正曲线时,最低实验点分析物的量值并不在零点,而在文章中将线性范围写成0～x,这是不严肃的做法。我们知道,测定低于分析方法检出限的量值,不能给出可靠的定量结果,因此,不能随意将校正曲线的线性下限延至0。

4 校正曲线应用

在本节讨论用校正曲线计算分析物量值之前,先看一个示例,用紫外分光光度法测定苯甲酸,校正曲线A=7.40+0.0733c,r=0.9989。分析样品,6次测定平均值是8.125μg/g,单次测定标准偏差0.0848。RSD=1.04%。按照习惯的做法,大多数分析人员都是这样报告实验结果。如果仔细加以分析,有些问题就值得斟酌了。在此例中,测定值的标准偏差完全由6次重复测定决定,与建立的校正曲线质量无关。

分析人员知道,校正曲线是计算样品测定量值的基础,建立校正曲线的质量直接影响由该校正曲线计算被测定分析物量值的质量。从统计的角度考虑,建立校正曲线y=f(x)的误差,会间接传递到分析样品的量值上。由分析信号测定值y0计算x0的标准偏差为

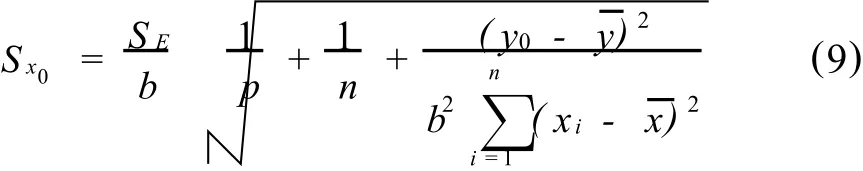
因此,在报告样品的测定结果时,只报告样品p次重复测定的标准偏差,而不考虑校正曲线的标准偏差SE的影响显然是不合理的。

在报告苯甲酸出的结果时,标准偏差0.0848,标准偏差有效数字取3位。分析人员都知道,重复测定次数越多,有效数字位数可以多取,究竟取多少位,是由标准偏差的精密度决定。标准偏差的精密度由下式计算,

式中p是重复测定次数。当p=6,Ss=0.316s,Ss/S=31.6%,就是说在十位数已是不确定了,有效数字最多只能取2位。由式(10)知道,当p≥51,Ss/S≤10%,个位数是不确定的,有效数字最多可取3位。在通常的例行分析中,只进行少数几次重复测定,标准偏差的有效数字最多只能取2位。按照GB/T 8170-2008,数值修约规则与极限数值的表示和判定[4],凡标准中对测定值有极限值规定时,均采用全数值比较法,涉及安全性能指标和计量仪器有误差传递的标准或其他重要指标,应优先采用全数值比较法,以避免通过数字修约将不合格的数据判为合格的数据。在本示例中,标准偏差取0.085。相对标准偏差取RSD=1.1%。

在苯甲酸示例中,报告结果给出的参数也不完备,没有给出必要的参数。表述测定结果应包括5个基本参数:(1)等精度测量给出算术平均值,非等精度测量给出加权平均值,平均值表征测定值的集中趋势;(2)等精度测量给出测定值的标准偏差或并合标准偏差及其相对标准偏差,非等精度测量给出加权标准偏差,或者给出不确定度,标准偏差、不确定度表征测定值的分散性;(3)置信程度(置信度或置信范围),不给出置信程度不便于对测定结果进行检验;(4)重复测定次数,它不仅与置信系数取值有关,也表征了经济效益;(5)测定数据的正确表示,遵守数字修约规则。

测定结果可用置信区间(式11)或不确定度(式12)的形式表示:

现在所发表的一些不确定度评定文章中,忽略了斜率和截距不确定度对总不确定度的贡献。从统计的观点看,校正曲线的斜率和截距随不同批取样是变动的,应该将其不确定度估计到总不确定度中。实践经验也证明,即使使用同一标准系列,不同批取样建立的校正曲线的斜率和截距是有变化的。有时斜率和截距的不确定度在总不确定度中占有显著的比例,如在火焰原子吸收光谱法测定铜精矿中银,总相对标准不确定度为0.024,校正曲线拟合标准不确定度是0.021,占总相对标准不确定度96%。而在校正曲线不确定度中,斜率和截距不确定度是0.0066,占29%。由此可见,在不确定度评定中,不能忽略斜率和截距不确定度的贡献。

5 结语

正确建立和应用校正曲线是仪器分析中获得准确测定结果的基础。建立校正曲线实验点的数目不少于5点,实验点的合理分布应该是校正曲线中央布点可稀疏些,校正曲线两端区域实验点布置密一些,对于5个实验点,在校正曲线中央布一个实验点,在靠近低端、高端各布两个相互邻近的实验点。校正曲线发生变动,用单点或两个实验点标定是不可取的,最好是将原实验点和新标定点合并重新制作校正曲线。在总测定次数相同的情况下,适当增加实验点数目减少每个实验点的重复测量次数,以利于提高校正曲线的整体稳定性。

校正曲线的动态范围与线性范围是有区别的,不能混淆。不能随意将校正曲线的线性范围延至零浓度,建议用校正曲线截距而不用零浓度点的值扣‘空白’。校正曲线中央的精密度优于校正曲线的两端的精密度,在测定样品时应尽量利用校正曲线的中央区域。由校正曲线计算样品中分析物的测定量值,不能只由分析物的重复测定次数计算测定量值的标准偏差,还应该考虑校正曲线标准偏差对测定值标准偏差的影响。在报告测定结果应给出测定值的置信区间或不确定度,在评定不确定度时应考虑校正曲线的斜率和截距变动性对总不确定度的贡献。在表述测定结果时,必须遵守有效数字的修约规则,在通常例行分析中,重复测定次数较少,标准偏差的有效数字最多只能取2位,相对标准偏差的修约,只进不舍,不允许通过数字修约将不合格的数据判为合格的数据。

[1]邓勃.分析测试数据的统计处理方法[M].北京:清华大学出版社,1995,24:105-118,308-312.

[2]Massart D L,et al.Chemometrics:a textbook[M].Oxford:Elsevier,1988:75-92.

[3]郑用熙,编著.分析化学中的统计方法[M].北京:科学出版社,1986:220-258.

[4]中国国家标准化研究院.GB/T 8170-2008数值修约规则与极限数值的表示和判定[S].北京:中国标准出版社,2008.

The Discussion on Some Problems with Construction and Application of Calibration Curve

DENG Bo
(Chem istry department,Tsinghua University,Beijing100084,China)

Most of the instrumental analysismethods are relative measurements and they require to establish some relationships between signals and quantity of analytes in order to obtain exact resultsof determination.Thus,constructing a right calibration curve is the basis to obtain accurate results from an instrumental analysis.In this paper,the construction,standardization and p ropertiesof calibration curves including the characteristic of central experimental point,p recision,confidence interval,dynamic and linear range of a calibration curve,etc.were introduced in detail.Some p ractical p roblem s concerning with the app licationsof calibration curves,such as calculation of p recision,determination of the significant figure of standard deviation as well as exp ression of determination results,etc.were discussed.

calibration curve;confidence interval;linear range;dynam ic range;significant figure

O657

A

2095-1035(2011)03-0001-07

10.3969/j.issn.2095-1035.2011.03.0001

2011-02-11

2011-03-12

邓勃,男,教授,主要从事光谱分析。E-mail:dengbo@mail.tsinghua.edu.cn