基于分形理论的三维模拟地形仿真
俞 静,石晶晶
(1.西南交通大学信息科学与技术学院,四川成都 610031; 2.西南交通大学电气工程学院,四川成都 610031)
0 引 言
山脉、平原和沙滩等类地形可以说是自然界中最为复杂的景物.而在虚拟现实技术中,将虚拟场景架设在连绵起伏的山脉、平原和沙滩等自然环境中,可以使虚拟场景的逼真度大幅提高.由于具有三维真实感的地形能够逼真地反映真实世界,所以三维真实感地形的绘制方法一直是国内外计算机图形学领域研究的热点.
目前,三维真实感地形的生成分为两类:真实地形和模拟地形.真实地形是现实世界中真实地形的再现,具有非常高的真实度,对于真实地形的构造,通常采用经纬度线构成的规格化网格体逼近的方法,其关键技术在于获取网格点的有关参数,包括它的经纬度、高程和颜色等数据.而在一般的虚拟现实场景中,三维地形只需满足感官上的要求即可,在这种情况下,可以采用模拟地形.模拟地形通常采用随机生成的方法或采用分形法生成,图形生成的速度较快.本文以OPENG L和VC++为基础,并基于分形理论,利用改进的Diamond-Square算法完成模拟地形的三维地形仿真.
1 细节层次技术及分形理论
细节层次技术的思想,是指对同一个场景中的物体使用具有不同细节的描述方法,从而得到一组模型供绘制时选择使用.层次细节简化技术在不影响画面视觉效果的条件下通过逐次简化景物的表面细节来减少场景的几何复杂性,从而提高绘制算法的效率[1].细节层次技术通常对每一个原始多面体模型建立几个不同逼近精度的几何模型,与原模型相比,每个模型均保留了一定层次细节.在绘制时,根据不同的标准选择适当的层次模型来表示物体.通常的做法是把一些不重要的图元(顶点、边和三角形)从多边形网格中移去.不过,在对同一物体简化后,物体在旋转、平移等运动过程中因模型的转换而产生形状差异.
1973年,Mandelbrot首次提出了分数维与分形几何的设想,其研究对象是自然界和非线性系统中出现的不光滑和不规则几何形体.由于分形关注的是物体的随机性、奇异性和复杂性,因而具有细节无限以及统计自相似性的典型特征.它采用分形曲线,利用自然景物的轮廓具有“自相似”的特征,能够得到逼真的效果,从而解决了使用光滑曲线这类不能进行微分计算的曲线对海岸线、山的轮廓描述时带来的失真问题.分形理论的出现为地形仿真的发展注入了强大的动力,由分形曲线发展而来的分形曲面可以较好的描述地形地貌.另外,用分形方法产生的三维模型能完好地保持模型的拓扑结构,因而具有良好的反走样效果,只是在精细结构上有一定差别.
2 Diamond-Square算法及改进
2.1 Diamond-Square算法
Diamond-Square算法由Fourniew等[2]提出,其又称为“钻石—四边形”算法.Diamond-Square算法的具体步骤如图1所示.

图1 Diamond-Square算法原理图
图1中,(1)为原始的正方形,正方形的4个顶点依次为A、B、C、D,假设其高度分别为 hA、hB、hC和hD.经过第一个Diamond步后,生成正方形的中点O如图1(2)所示,其中黑色圆点表示新生点,灰色圆点表示已知点.此时,正方形中点的高度值为 h0,

式中,RO为随机变量,通常采用均值为0,方差为1的正态随机分布函数来产生.
然后,进行第一个Square步,这一步分别生成正方形各边中点,如图1(3)中的点 p和点q,其高度值hp、hq为,
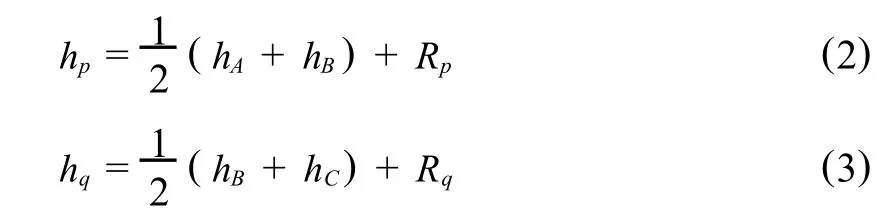
同样的,式中的 Rp和Rq为随机变量,取值与RO相同.
依次类推可以计算出每条边的中点的高度值.这样,完成一个完整的Diamond-Square步骤之后,由4个已知点变为了9个已知点.图1(4)、(5)是第二个Diamond-Square步骤,第二步与第一步有两点不同.首先,现在有4个正方形而不是一个,因此必须计算4个正方形面的中心;其次,生成随机数的范围已经被减小了,图1(4)在这一步得到的4个正方形中心值显示为黑色.完成了上述步骤之后,由9个已知点变成了25个已知点.
由此可见,采用Diamond-Square算法将一个正方形经过单独一次细分过程,可得到4个正方形.第二次细分过程可得到16个正方形,第三次细分过程可得到64个正方形……正方形数目等于2n+2,其中,n为细分过程的迭代次数.如果分配更大的数组,可以将迭代过程进行更多遍,每一遍将加入更多的细节.所以,采用Diamond-Square算法对地形的生成速度很快,而且实现非常容易,且可以生成任意分辨率的三维地形.
2.2 改进的Diamond-Square算法
采用Diamond-Square算法实时绘制三维地形虽然有诸多优点,但该算法也存在一定的局限性.采用该方法生成的地形表面容易产生明显的“褶皱”和“尖峰”[3,4].基于此,本文提出一种改进的Diamond-Square算法,其可以在一定程度上改善生成的地形表面出现“褶皱”和“尖峰”的现象.
算法的改进思想就是在每一次根据构成网格的4个角的高程计算网格中心点和正方形四边中点的基础上,增加由地形高程的自相似参数 H和方差δ构成的补偿项.
地形高程的自相似参数 H反映了地形表面的复杂程度和粗糙度.参数 H值越小,表明地形越复杂、越粗糙,反之越平滑.地形高程的方差δ则反映区域地形整体形状的起伏特征,δ的值越大,地形起伏就越大,反之就越小.地形的自相似参数 H和方差δ采用分形布朗运动的原理来提取,

令,


则,式(6)两边取对数可得,

由此可知,lgE(|f(x+△x)-f(x)|)与 lg‖△x‖与成线性关系,采用最小二乘法得其直线回归的函数为,
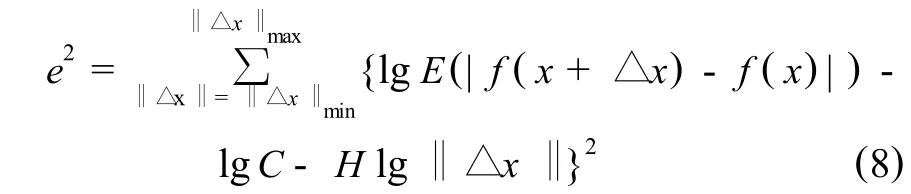
式(8)最小化即可求出参数 H和δ.
同时,由分形布朗运动的性质和递归中点细分的原理可得,

现在加入补偿项sk可得,
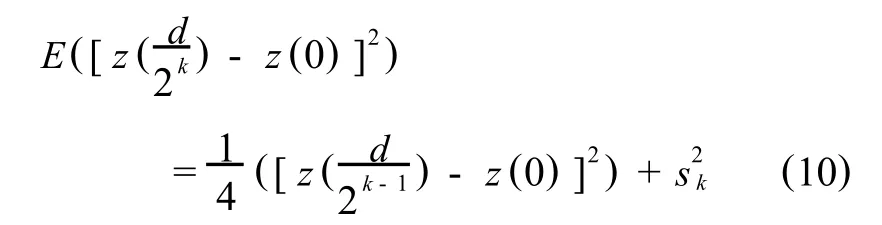

其中,gauss()函数服从标准正态分布,d为网格间距.
式(10)化简可得,
3 仿真实验
在仿真实验中,仿真实现的硬件环境为,英特尔酷睿2 T6600双核处理器,2 G B内存,512 MB独立显卡;软件环境为,Windows XP专业版下Visual C++ 6.0及三维图形标准OpenG L 2.1.
三维模拟地形的仿真结果如图2所示.

图2 三维模拟地形仿真结果
图2中,在假设只有4个初始点的情况下生成三维分形地形.图2(a)为经过第一步Diamond-Square算法步骤后的结果,图2(b)、图2(c)、图2(d)的迭代次数依次为2,5,7.从图2中可以明显的看出,随着迭代次数的增加,生成的模拟地形中点的个数是成指数增长的,并呈现出真实地形的粗糙感.
在图2中,地形自相似参数 H值均为0.7.下面改变 H值,仿真结果如图3所示.

图3 采用不同 H值的模拟地形仿真结果
图3(a)为采用改进的Diamond-Square算法迭代5次,地形自相似参数 H为0.9的三维地形生成图,图3(b)同样为迭代5次,地形自相似参数 H为0.6的三维地形生成图.由图3可知,当 H值越大时,采用改进的Diamond-Square算法生成的三维模拟地形越平滑,当H值越小时,生成的三维模拟地形已经出现了明显的凸起和沟壑.因此,在实际的应用中可以根据需要调整 H值来生成满足实际需要的三维模拟地形.
图4为使用改进的Diamond-Square算法生成三维模拟地形并赋予纹理贴图后的渲染图.在图4中,三维模拟地形在高度值低的地方呈现出黑色,高度值高的地方呈现出灰色.此外,在具体的工程实际应用中,三维模拟地形的地形纹理图片可根据实际需要选取,也可以通过在程序中进行设置而使地形的高程呈现出不同的颜色.

图4 三维模拟地形渲染效果图
4 结 论
利用分形理论生成的三维模型地形,首先需要静态拼嵌高程数组来产生逼真程度很高的静态地形,然后根据需要赋予不同的迭代次数和相关参数,从而生成具有动态特性的三维真实感地形图.仿真实验表明,采用改进的Diamond-Square算法,提取三维模拟地形的自相似参数 H和方差δ构成补偿项加入有序的迭代步骤,可有效地改善直接采用Diamond-Square算法生成三维模拟地形时产生的“褶皱”和“尖峰”现象.
[1]祝清鲁.大规模场景中LOD技术的研究与应用[D].北京:北京邮电大学,2009.
[2]和平鸽工作室.OpenG L高级编程与可视化系统开发[M].北京:中国水利出版社,2005.
[3]曹为刚.基于OpenG L的三维地形可视化技术与实现[J].四川建筑,2006,4(2):91-95.
[4]李捷,唐泽圣.三维复杂模型的事实连续多分辨率绘制[J].计算机学报,1998,6(6):481-491.
[5]姚慧敏,崔铁军.基于四叉树的LOD地形模拟及其数据组织方法研究[J].地理信息世界,2007,12(6):56-59.
[6]聂永丹.实时虚拟环境几何、运动和行为LOD技术研究[D].大庆:大庆石油学院,2009.
[7]刘 扬.分布环境下的海量三维地形可视化关键技术研究[D].北京:北京师范大学,2008.

