基于重要性联系度粗糙集模型的规则提取

李 立

(安庆广播电视大学,安徽安庆 246003)

0 引 言

近年来,将粗糙集理论和粗糙集对分析中的联系度相结合的研究成为了一个热点[1-3],有学者在限制容差关系模型的基础上,通过引入联系度的概念[4],建立了一种基于联系度的粗糙集扩展模型[5].本文对该模型做了改进,加入了条件属性存在重要性差异的因素,以决策属性对条件属性的依赖程度作为条件属性的重要性,定义了不完备决策表中对象间的重要性联系度,进而定义了相应的重要性联系度容差关系,提出了基于重要性联系度的粗糙集扩展模型.同时,在此模型中给出了对不完备决策表进行属性约简和规则提取的算法,并进行了实验验证.

1 基本概念

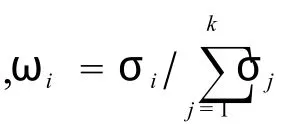
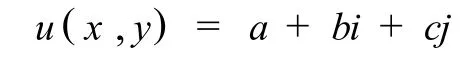
其中,a+b+c=1.

定义2 不完备决策表,S=(U,C∪D,V,f), A⊆C,给定一个阈值θ,则定义重要性联系度容差关系LWR(A,θ)为,(x,y)∈LWR(A,θ)⇔(a≥θ,且c=0)或(x=y).

定义3 对象 x的重要性联系度容差关系类,

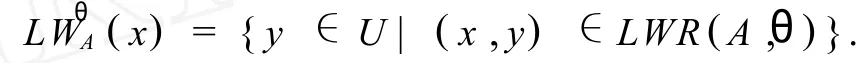
2 属性约简

定义4 不完备决策表,S=(U,C∪D,V,f), C为条件属性集合,D为决策属性,设 C′⊆C,若POSC′(D)=POSC(D),且C′中的任意属性都是必要的,那么C′称为基于重要性联系度的粗糙集模型在不完备决策表中的属性约简.

算法1 基于重要性联系度容差关系的属性约简算法如下:

输入:不完备决策表,S=(U,C∪D,V,f),C为条件属性集合,D为决策属性集合.

输出:S的属性约简,

yj= φ;

计算每个条件属性的重要性以及对应的权值,分别存放在数组sita和qz中;计算每个对象的重要性联系度容差关系类,存放在数组 LW中;计算POSC(D);

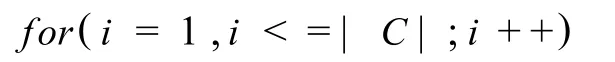
{令 C′=C-{ci}};

计算C′中各条件属性重要性对应的权值;计算在集合 C′上,每个对象的重要性联系度容差关系类;

计算 POSC′(D);

若 POSC(D)≠POSC′(D),则:

yj= yj+{ci};}

while(true)

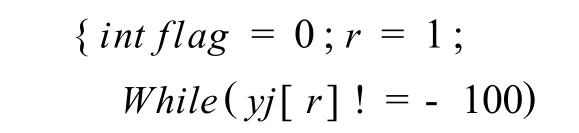
{判断yj中的每一个属性cj是否是必要的,若cj不必要,则,

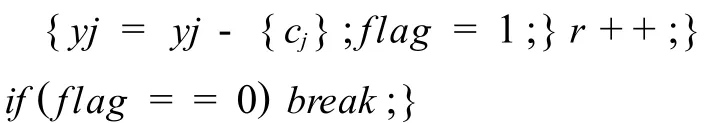
例1 对于表1所示的不完备决策表S,求其属性约简.

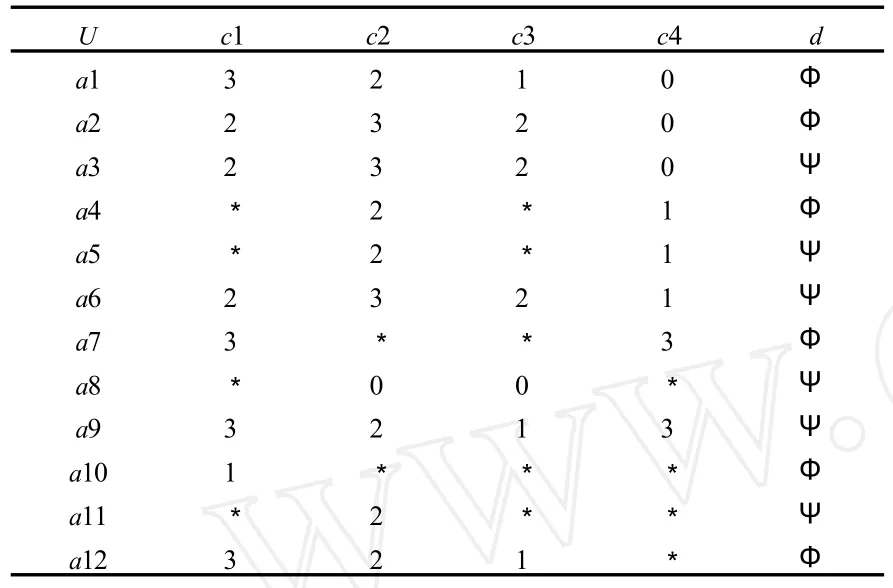
表1 不完备决策表S

由表 1可计算出:C—θΦ ={a1,a10},C—θΨ = {a6,a8,a11},由此得,POSC(D)={a1,a6,a8,a10, a11}.去掉条件属性c1,记 C′=C-{c1}={c2,c3, c4},重新计算各条件属性重要性对应的权值,得, ω2=1/2,ω3=0,ω4=1/2,若取θ=0.6,则各对象的重要性联系度容差关系类为:

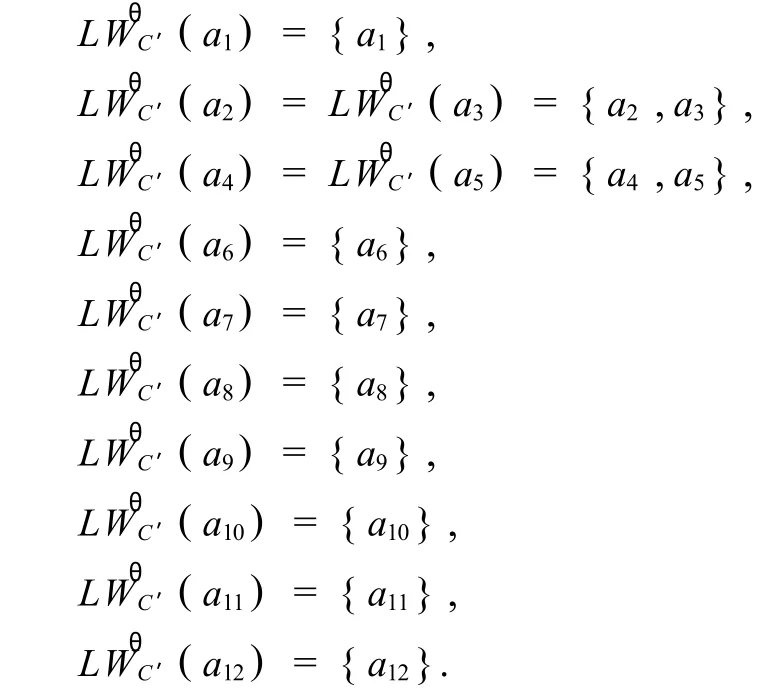
由此得,

所以,条件属性c1是必要的.

同理可计算得,属性c1、c2和c4是必要的;属性c3是不必要的.

由此可得,表1表示的不完备决策表S的属性约简为{c1,c2,c4}.

3 规则提取

定义5 不完备决策表,S=(U,C∪D,V,f),其中,A⊆C,则其每个对象 x的广义决策函数为,

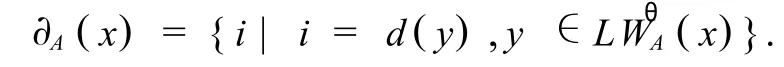
定义6 对于对象x,决策规则关于条件属性集的一致程度为,

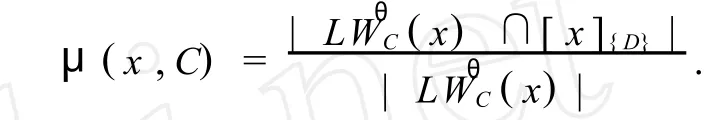
算法2 基于重要性联系度容差关系的规则提取算法如下:

输入:不完备决策表,S=(U,C∪D,V,f),C为条件属性集合,D为决策属性集合.

输出:S的决策规则.

根据算法1对不完备决策表进行属性约简,得约简,P={c1,c2,…,cn}.

{计算出μ(x,P)和 ∂P(x);Q= P;

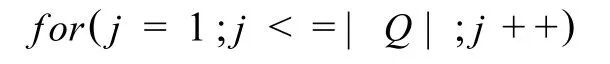
{k=Q[j];如果对象i的属性cj为空值,则:

{在 Q中删去属性cj;|Q|--;j--;}

如果对象 i的属性cj不是空值,则:

{计算μ(x,Q-{cj})和 ∂Q-{cj}(i);

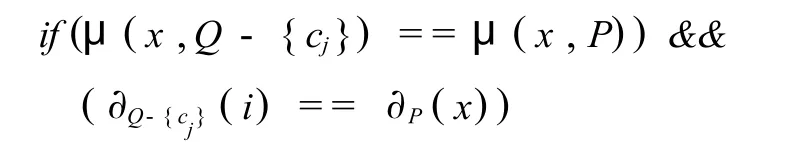
{删去属性 cj;|Q|--;j--;}

else{保留属性 cj;}}}

{输出对象i对应的决策规则:∧(c,v)→

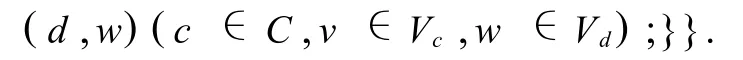
例2 确定对于表1所示的不完备决策表S,提取其属性约简后的决策规则.

由例1可知,表1中不完备决策表的属性约简为,{c1,c2,c4},则,Q={c1,c2,c4}.

对于对象 a1,μ(a1,Q)=1,∂Q(a1)={Φ}, μ(a1,Q-{c1})=1=μ(a1,Q),∂Q-{c1}(a1)= {Φ} = ∂Q(a1).所以,Q = {c2,c4},μ(a1,Q -{c2})=2/3,μ(a1,Q-{c4})=1/2.因此,约简后提取出的决策规则为,

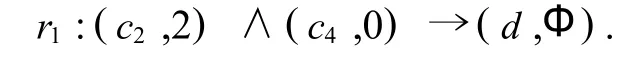
同理,考察其他的对象可以提取表1所示的不完备决策表中的决策规则:

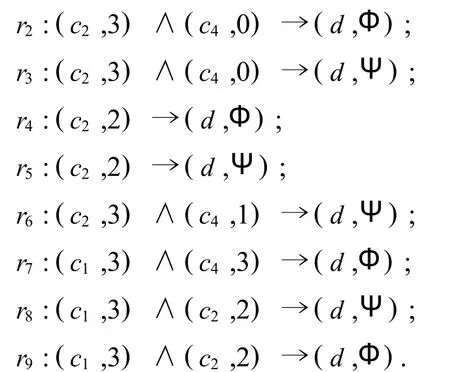
4 实验结果与分析

4.1 实验结果

为了验证算法1和算法2的正确性和有效性,我们利用Visual C++6.0编写了程序,并在计算机上实现了这2个算法,同时,采用UCI机器学习数据库中的数据集进行了测试.

程序运行的界面如图1所示,输入对象的个数、条件属性的个数以及设定的阈值,单击属性约简或者规则提取的按钮,则显示相应的结果.

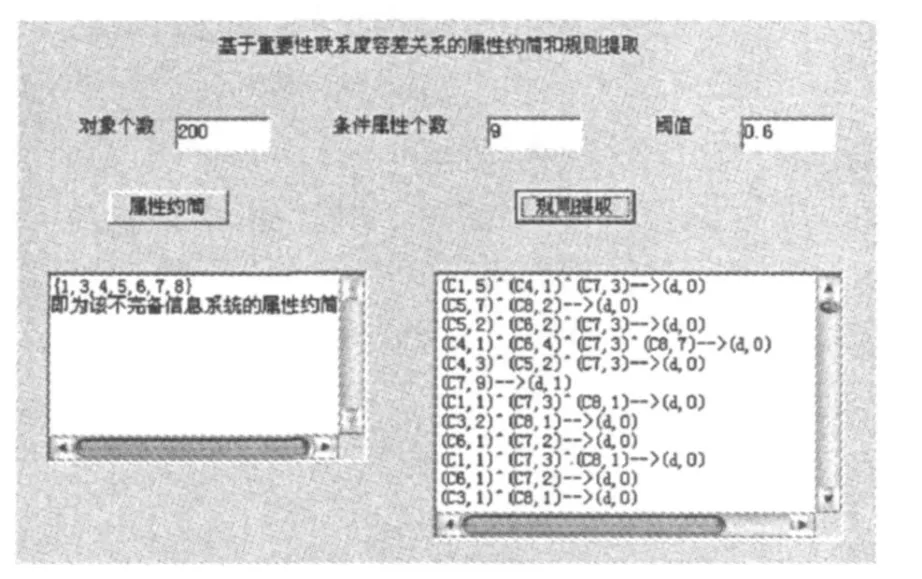
图1 属性约简和规则提取程序运行界面

若设定阈值为0.6,从UCI机器学习数据库中选取了4个数据集[5],实验结果如表2所示.

表2 实验结果

4.2 分 析

从表2的实验结果来看,基于重要性联系度的粗糙集模型在进行规则提取时,由于考虑了条件属性重要性的差异,并尽量保留重要性高的属性,所提取出来的规则更有实际利用价值.同时,在计算各对象的重要性联系度容差关系类时,可以直接输入希望的阈值,更符合设计者的主观要求.而如何更合理地选取阐值以及如何更合理地评估属性的重要性则是需要进一步研究的问题.

[1]刘富春.变集对联系度的扩充粗糙集模型及其属性约简[J].计算机科学,2006,33(3):185-187.

[2]陈蓉素.不完备信息系统中的集对粗糙集模型分析[J].计算机工程与应用,2009,45(16):63-65.

[3]陶志,戴慧君,张艳.不完备信息系统中集对粗糙集模型分析[J].计算机应用,2008,28(7):1684-1685.

[4]黄兵,周献中.不完备信息系统中基于联系度的粗集模型拓展[J].系统工程理论与实践,2004,24(1):88-92.

[5]黄兵,李华雄,周献中.不完备联系度粗糙集模型的知识约简[J].计算机工程,2008,34(11):19-20.