Winkler地基上脱空和无脱空简支矩形薄板振动特性分析

康怀,董 杨

(重庆交通大学土木建筑学院,重庆 400074)

0 引 言

在实际工程中,许多板的振动问题与弹性地基有关,比如土建工程中的的基础地板、公路桥面板、工业地坪等建筑基础工程.弹性地基上板的振动问题实质是板件与三维无限弹性介质的动力相互作用问题,该问题即便在线弹性范围内也一直被业界认为是相当困难的研究课题,对此,Saha[1]研究了基于Winkler地基的薄板自由振动问题,G orman[2,3]利用叠加法分析了弹性矩形薄板的固有频率,并得到了具有混合边界条件矩形板的自由振动问题的解析解,Matsunaga[4]和Vallabhan[5]等研究了弹性地基板的自由振动问题,Rajalingham[6]利用梁函数法分析了弹性矩形薄板的振动问题,钟阳[7]利用几何法分析了弹性矩形薄板的振动问题,黄炎[8]应用一般解析解对具有中间支承的矩形板自由振动进行了分析求解,张英世[9]分析了Winkler地基上矩形薄板的自由振动和强迫振动问题.同时,大量工程实践证明,弹性地基板的振动问题采用Winkler模型在实际工程中具有广泛的适用性.在工程中,因施工或其他原因造成地基板脱空难以避免,因而,对脱空板的研究同样具有重要的工程意义.然而,对Winkler地基上脱空薄板的振动问题的研究远少于无脱空薄板.基于此,本文对Winkler地基上底面部分脱空四边简支矩形薄板(下文简称脱空板)和Winkler地基上无脱空四边简支矩形薄板(下文简称无脱空板)的振动问题进行了研究.在研究中,根据力的平衡原理,将脱空板的自由振动问题转化为无脱空板的受迫振动问题,并获得了相应的解.

1 Winkler地基上薄板的固有频率

Winkler地基上矩形薄板自由振动的微分方程可表示为,

式中:▽4为重调和算子,ω为振动的任一瞬时位置量起的挠度,m—为单位面积板的质量;对无脱空板, k为Winkler地基系数ks,D=Eh3/[12/(1-μ2)]为板的抗弯刚度,h为板厚,μ为泊松系数,E为材料的弹性模量.

针对四边简支矩形无脱空板(见图1),方程(1)

图1 无脱空板示意图

的通解可表示为,

式中,Wj(x,y)为板的振型函数.

综合式(1)、(2)可得,

式中:Tj(0),T·j(0)为函数 Tj(t)的初参数,由振动初始条件和边界条件确定;Yj(0)=0,Y″j(0)=0; Ψ0～ Ψ3为影响系数,其定义与常数α,β及2(jπ/a)2,(jπ/a)4+(k-m—ω2j)/D有关.以下仅讨论m—ω2j-k＞0的情况[9],此时,α=

将式(3)、(4)代入式(2),并根据边界条件, Yj(0)=0,Y″j(0)=0,可得弹性地基四边简支板的挠度函数,其频率方程由文献[10]给出,

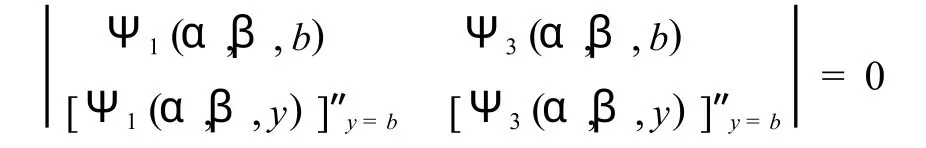
将Ψ1,Ψ3展开为泰勒级数,代入上式,可得板的固有频率,

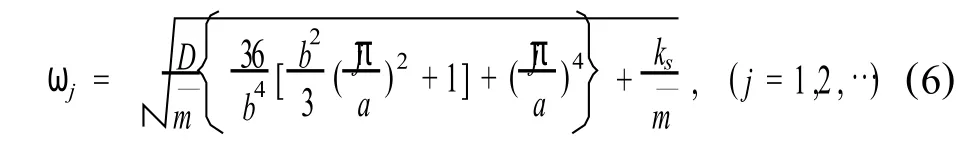
由于脱空区地基系数ks=0,由式(6)可以分析得出,脱空板固有频率低于无脱空板固有频率,脱空板的脱空区和非脱空区具有不同的固有频率.因此,脱空板具有局部振动特性.

2 Winkler地基上脱空矩形薄板振动控制方程求解

脱空板在振动过程中地基反力仅作用于板与地基粘合区,脱空区无地基反作用力,其自由振动微分方程如式(1)所示,其中,

式(1)经适当数学变换可转化为,

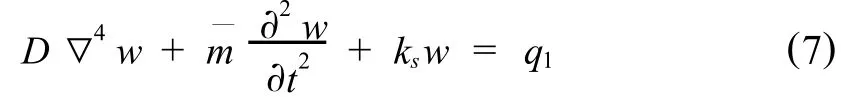
根据力的平衡原理,在脱空板的脱空面域内施加一对大小等于地基反力的反作用均布力,力的方向规定为,在板的脱空区底部均布力方向与地基反力相同,表面均布力与之相反(见图2).于是,脱空板的自由振动问题可转化为无脱空板受局部均布动力荷载的受迫振动问题.

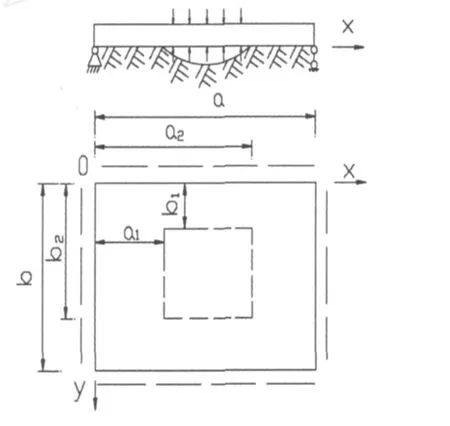
图2 脱空板地基反力作用示意图

首先,将动力荷载展为振型函数的级数,简支矩形板振型函数采用Naiver双三角级数,并将方程的解取为振型函数与时间函数乘积的级数和,式(7)化简得,

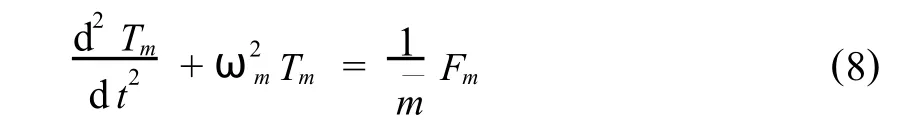
将振型函数与动力荷载进一步转化为如下形式的级数,

其中,τm(t)是任一特解.

由式(8)、(9)、(10)可解得,

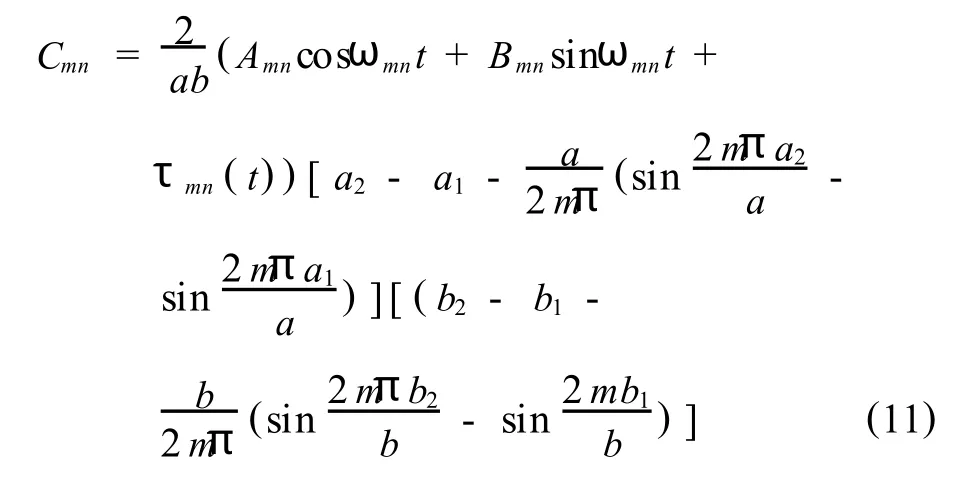
联立式(8)、(10)、(11)可得微分方程(10)的特解为,

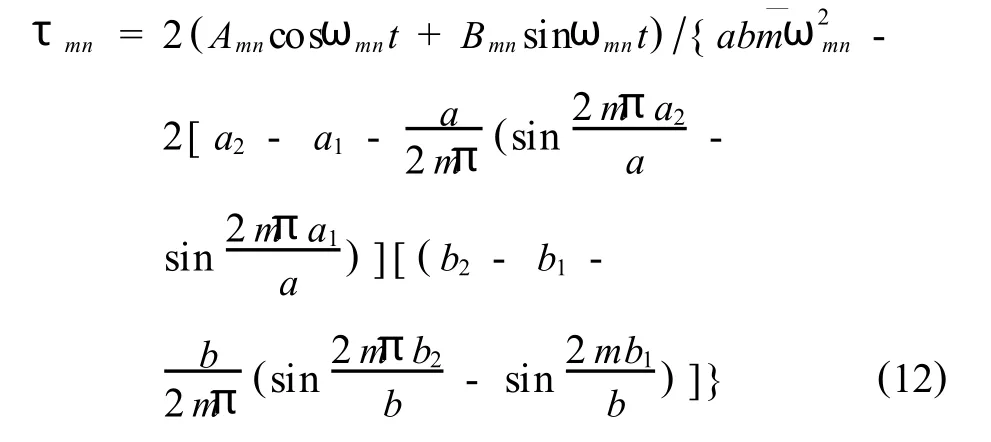
将(12)式代入(9)式并由板在脉冲激励下振动的初始条件可求系数Amn和Bmn,即得挠度的解,

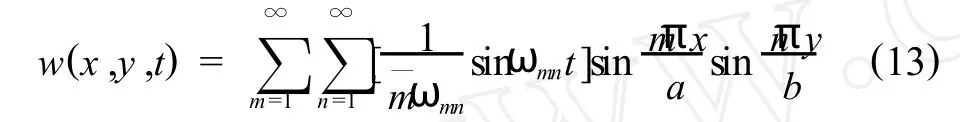
因此,板上测点(x,y)在模态(m,n)下的频响函数为,

3 仿真分析

3.1 模型描述

在仿真实验中,我们首先预制两块相同薄板,尺寸为 a=60 cm,b=60 cm,h=1 cm;材料参数为,弹性模量 E=50 G pa,泊松比μ=0.2,单位面积质量 m—=21 Kg/m2,Winkler地基系数 ks=2.3×107N/m3;支承设置为,无脱空板底面全部与地基密实粘结,脱空板底面中部预设40 cm×40 cm的脱空区,底面其余部分与地基密实粘结,板为四边简支约束.

3.2 脱空板、无脱空板仿真分析

在ANSYS分析软件中分别建立脱空板(见图3)和无脱空板(见图4)的有限元模型,地基单元采用弹簧单元 COMBIN40.图5、图6分别为脱空板的第1、4阶模态振型.在分析中,对脱空板的分析所得到的固有频率为脱空板全局固有频率.

表1为采用ANSYS软件分析得到无脱空板和脱空板的前6阶频率值.将板的参数代入式(6),可计算得到板的各阶固有频率.无脱空板的第1阶固有频率ω1w=1 783.2 Hz;脱空板的振动含有板脱空区在四边固支的支承条件下的局部振动和整板在简支边界条件下的全局振动,是全局与局部的耦合振动,采用式(6)近似计算其脱空区第一阶固有频率ω1t=267.6 Hz,低于整板全局第1阶固有频率.从计算结果来看,仿真分析与理论计算在低阶模态下吻合的得较好,而高阶模态下,偏差较大.从表1也可以看出,脱空板各阶固有频率远小于无脱空板,这是由于脱空板因中部脱空设置而导致板刚度低于无脱空板,使得振动固有频率降低.

图3 脱空板有限元模型

图4 无脱空板有限元模型

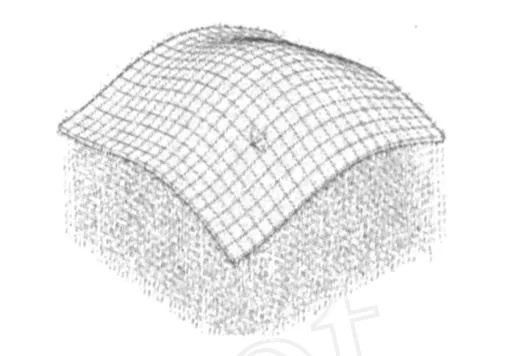
图5 脱空板第1阶振型

图6 脱空板第4阶振型

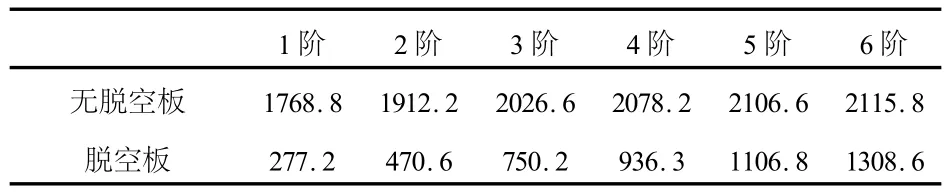
表1 无脱空板和脱空板非脱空区的前6阶频率值(Hz)

4 实验分析

在实验中,我们在无脱空板和脱空板板面分别均匀布置9×9=81个测点,采用本点激励本点采集方法,用力锤对板施加脉冲激励,由加速度传感器采集各测点加速度响应信号.同时,采用DH2538动态信号采集与分析系统对响应信号进行分析,得到板振动幅频特性曲线,再从中提取相应的幅值与频率.

4.1 无脱空板振动频谱特性

图7、图8是无脱空板板面上测点的幅频图,从各测点采集得到的幅频图可以看出,无脱空板的第1阶共振峰对应的频率范围为1 560～1 700 Hz,实验结果接近于与理论计算和有限元分析结果.

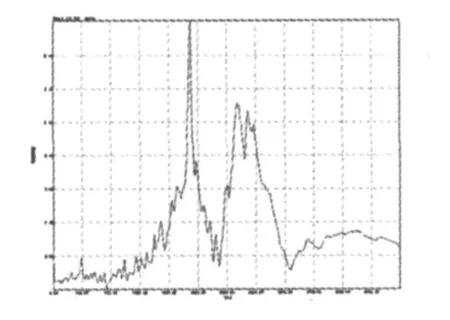
图7 无脱空板6号测点幅频图

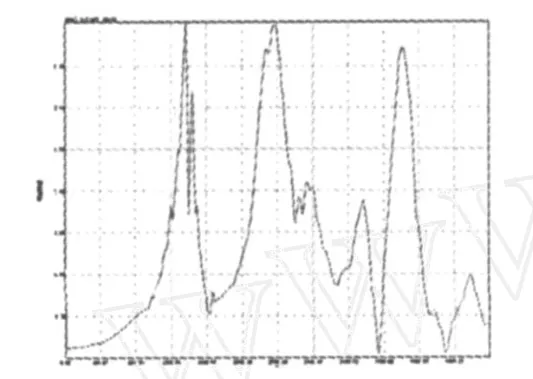
图8 无脱空板9号测点幅频图

4.2 脱空板振动频谱特性

图9、图10分别是脱空板上脱空区和非脱空区测点的幅频图.

图9 脱空板脱空区测点(41号)幅频图

图10 脱空板非脱空区测点幅频图

从图9、图10可以看出,在板的脱空区第1阶共振峰发生在240～250 Hz频带区间内,而非脱空区在0～550 Hz的分析频带内没有板基频共振峰出现.脱空区和非脱空区振动为非谐频振动,表明脱空板的振动含有局部振动成分.此外,由41号测点的幅频图可以分析出该测点第1阶无量纲共振峰值为0.4,该测点位置为板的中心,其频响函数根据相应模态由(14)式计算,结果显示,低阶模态下分析计算与实验检测幅频特性相符.

5 结 论

由上述公式推导、仿真分析和实验测试可以得到以下结论:

(1)针对Winkler地基上的脱空板,根据力的平衡原理,可将脱空板的自由振动问题转化为无脱空板受局部均布动力荷载的受迫振动问题,实验验证了该问题解的正确性.

(2)Winkler地基上脱空板的振动,在脱空区和非脱空区模态参数存在着明显的差异性.因此,脱空地基板的振动具有局部振动特性,板的全局与局部振动机理有待进一步研究.

(3)Winkler地基上无脱空板和脱空板的模态分析显示,无脱空板各阶固有频率远高于脱空板同阶固有频率.

(4)本文提出的方法可应用在对刚性路面板、土建工程中的地基板等基于振动法的脱空检测中.

[1]Saha KN.Dynamic Stability of a Rectangular Plate on Nonhomogeneous Winkler Foundation[J].Comput Struct,1997,63(6): 1213-1222.

[2]G orman D J.An Exact Analytical Approach to the Free Vibration Analysis of Rectangular Plates with Mixed Boundary Conditions [J].Journal of Sound and Vibration,1984,93(1):235-247.

[3]G orman D J.Free Vibration of Rectangular Plates[M].New Y ork:Elevier Inc,1982.

[4]Matsunage H.Vibration and Stability of Thick Plates on Elastic Foundations[J].J Eng Mech,2000,126(1):27-34.

[5]Vallabhan C V G,Straughan W T,Das Y C.Refined Model for Analysis of Plates on Elastic Foundations[J].J Eng Mech,1991, 117(12):2830-2844.

[6]Bhat R C.Vibration of Rectangular Plates Using Plate Chareceristics Functions as Shape Function in the Raleigh-Ritz Method [J].Journal of Sound and Vibration,1996,197(3):263-281.

[7]钟阳,张永山.四边固支弹性矩形薄板的自由振动[J].动力学与控制学报,2005,3(2):66-70.

[8]黄炎,李道奎蔺文峰.具有中间支承的矩形板自由振动分析[J].振动与冲击,2007,26(5):23-26.

[9]张英世,王燮山.文克尔地基上矩形薄板的振动[J].水利学报,1997,42(5):71-77.

[10]曹志远.板壳振动理论[M].北京:中国铁道出版社, 1989.

[11]徐芝纶.弹性力学(下册)[M].北京:高等教育出版社, 2006.

[12]黄义,何芳社.弹性地基上的板、壳、梁[M].北京:科学出版社,2005.