补偿视角下的工程进度协调及其收益Shapley值法分配

钟波涛，丁烈云，，余明辉，周 迎

(华中科技大学 a.系统工程研究所;b.土木工程与力学学院，湖北 武汉 430074)

补偿视角下的工程进度协调及其收益Shapley值法分配

钟波涛a，丁烈云a，b，余明辉a，周 迎b

(华中科技大学 a.系统工程研究所;b.土木工程与力学学院，湖北 武汉 430074)

利用TCTP优化原理对工程施工进度协调进行分析，指出进度协调的本质，将进度协调区分为同一分包商主体任务间进度协调和不同分包商主体任务间进度协调。针对不同分包商主体任务间进度协调，将其视为自私理性主体的协作问题，提出工程进度协调的利益补偿机制，并在补偿机制的基础上建立合作博弈模型，利用Shapley值法对协调收益进行合理分配，促进协调各分包商自主加入进度协调。本研究对于促进分包商最大限度进度协调，降低施工成本，以及进度协调收益的合理分配提供了理论依据和操作规则。

进度协调;时间—费用优化;补偿机制;合作博弈;Shapley值法

一、引言

在现实工程中，承包商首先通过投标，与业主签订工程承包合同。然后将整个工程分化成许多工程任务，将它们分别委托给拥有专业技能的分包商。这些工程任务存在着各种逻辑关系(资源、时间等)和优先顺序，形成整个项目的实施过程。在工程的施工过程中，各种意外事件导致任务进度冲突，如材料设备供应脱节、现场土建和设备安装冲突、资金不到位等，都会影响到后续工程任务的施工。工程任务的分包商作为独立的实体，在经济利益的驱使下往往会根据自己的意愿(最小损失)来进行施工，造成了整个工程进度的不协调［1］。如何协调这种进度冲突，是项目管理的重要问题［2］。

当发生进度冲突时，现行的做法是由监理、业主、总承包商出面协调［3－4］，无论是监理、业主、总承包商，他们本身也是利益参与者，从经济学中“理性人”的角度考虑，在没有外来约束的情况下，他们在协调的过程中或多或少地为自己的利益着想，很难保证其公平公正的角色要求［5］。并且，大型工程项目涉及众多专业领域知识，总承包商等协调者的能力很难满足协调本身对各专业知识的需求［6］，加之信息不对称性等原因(分包商出于利益的考虑，会隐瞒真实进度信息)，协调者无法全面了解分包商的实际资源状况和成本信息，协调出来的方案损害了某些分包商的利益，分包商并非乐意接受这些协调方案，也因此延长工期、增加施工费用。

分包商是自治的实体，在进度协调中具有主观能动性，事实上施工过程中的很大部分协调工作是分包商自己承担，通过彼此协商得出的［6－7］。本研究的基本思路是:突破由监理/总承包商进行进度协调的传统模式，通过利益补偿与合理的收益分配机制，促进各分包商积极地加入自主协调，最大限度地降低施工成本，克服监理/总承包商协调存在的弊端。文章首先利用TCTP优化原理对问题进行分析，指出施工阶段进度协调的本质，将进度协调区分为同一分包商主体任务间进度协调和不同分包商主体任务间进度协调。将不同分包商主体任务间进度协调视为自私理性主体的协作问题，提出工程进度协调的利益补偿机制，并在补偿机制的基础上建立合作博弈模型，利用Shapley值法对协调收益进行合理分配，促进协调各分包商自主加入进度协调。

二、工程进度协调问题分析

(一)工程进度协调的成本分析

对于一项施工任务，当与之有关的其他条件确定后，都存在一个最优的任务进度工期，在进度协调过程中，对一项任务的任何不同的时间分配，偏离这一最优工期都会造成成本的增加［8－9］:压缩工期就意味着需要添加额外的资源或者提高资源的使用强度，导致费用的增加;延长任务工期也会引起管理费用等间接成本的增加，甚至导致资源闲置的损失。文献［10］将施工成本分为正常的直接费用、间接费用、压缩费用三类。本研究在此基础上还考虑任务在不同时间执行的费用差异，即同样的任务工期，在不同的开工时间执行，会引起额外的成本费用，我们称之为移动成本。按照任务的成本与任务时间的分配的关系，将任务成本分为四类:

ij直接费用，包括直接用于该任务的原材料、人工和设备等费用，仅与任务的工程量有关，记为

则执行一项任务的成本除去外，其他三类成本都与任务的执行时间有关，可见，任务在时间上的不同分配就会导致不同的施工成本。笔者的模型建立在四类成本构成基础之上。

(二)工程进度协调的本质

施工阶段工程进度的矛盾和冲突主要体现为施工任务在时间和空间分配上的平衡。在施工阶段工程设计方案已经确定，空间的分配不可能有大的改变，因此进度协调的主要途径在于改变施工任务在时间上的分配，即工程进度协调的本质是:通过调整施工任务在时间上的分配实现工程进度的协调［5］。显然，施工阶段意外事件引起的进度冲突协调也体现为相冲突的任务彼此在时间分配上的平衡。

按照任务所属分包商主体不同，可以分为同一主体任务间进度协调、不同主体任务间进度协调。由TCTP优化原理可知，不同的任务由于其成本构成不同，压缩相同的工期产生的费用不同，这给任务间进度的协调提供了潜在的空间和收益。同一主体任务间进度协调，可以通过时间—费用优化原理(TCTP)进行:依据一定的优先规则选择可以优先压缩的任务进行工期压缩，直到满足工期要求［10］。可以优先压缩的关键任务，通常是对质量、安全影响不大的关键工作;有足够资源储备的关键工作;因压缩而增加费用最少的关键工作等。由于在同一分包商主体内进行，这种协调不必考虑任务间利益转移，常采用动态规划、启发式智能算法等进行优化［8］。

不同主体任务间进度协调本质上也可以看作是这些属于不同主体的任务依据TCTP优化原理预示的潜在优化空间进行的一种优化过程。当施工过程中出现进度冲突时，各分包商就联合起来，进行这种彼此任务间的进度协调。不同的是，这种协调过程必须考虑主体的自利性、独立性、分散性等特点。任务在时间上的不同分配就会导致不同的施工成本，不同主体任务间进度协调常常伴随着利益在不同主体间的转移，协调是以利益为中心的，是自私理性主体的协作问题。

(三)工程进度协调的补偿策略和收益分析

当意外事件引起任务进度冲突时，分包商总是试图寻找一种成本最小的冲突解决方案，体现在任务的时间分配上，就存在两种选择方案:(1)加速赶工以按时完成;(2)延长工期。第一种方法会造成分包商自身的额外成本(压缩费用)，而第二种方法会造成承担后续活动的分包商的额外成本(或者是压缩费用、或者是移动费用等)。分包商在做出决定前，会评估这两种额外成本，选择造成较小成本的方案来完成任务，但是，这样对其后续的分包商们是不公平的，通过支付补偿金的方法能够较好地解决这一问题。下面以TCTP优化原理分析(在不影响理解下，这里仅仅考虑上述三种与时间分配有关的任务成本中的压缩成本后文同此解释)。

假设与是某一任务网络关键路径上紧前紧后关系的两个任务，分属分包商Subj与Subk。在施工过程中，由于分包商Subj执行任务的资源不能向预期那样满足需求，导致任务按照现有资源正常施工会产生△t的进度延误，与后续任务的进度计划冲突。分包商Subj存在两种选择:(1)加速赶工，保证按计划完成任务;(2)选择延期△t。前者会产生额外赶工成本，即压缩费用△t;后者会引起任务执行时间的缩短，假设分包商Subk不延迟其任务，分包商Subk也需要赶工△t时间，导致分包商Subk产生额外赶工成本，即压缩费用△t。理性的分包商Subk需要来自分包商Subj的补偿，理性分包商Subj会在支付补偿和加速赶工中权衡选择成本较小的方案。假设补偿费用仅仅包含其实际的额外成本△Costk△t，如果，表明任务的单位压缩成本高于任务Akl的单位时间压缩成本，分包商Subj选择将任务延迟△t时间，并支付给分包商Subk压缩成本补偿费用△Costk=×△t，从 而 节 约 额 外 成 本 △Utilityj=(×△t)－(△t)。在这一例子中，称为被协调任务，称为协调任务。对协调任务而言，在得到来自被协调任务的补偿后，其成本保持不变;对被协调任务而言，除去支付给协调任务的压缩成本补偿费用，还可以节约部分成本，节约的这部分成本就可以看作是进度协调的收益。

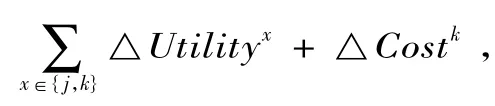
三、工程进度协调的合作博弈与收益分配

(一)工程进度协调合作博弈模型

前文已经指出，不同主体任务间进度协调常常伴随着利益在不同主体间的转移，协调是以利益为中心的，是自私理性主体的协作问题。合作博弈是一种解决多个独立利益主体协调行动产生收益分配问题的有效数学模型方法。当问题结局由多个利益主体行为共同确定时，若多利益主体协调行为产生的结局能带来更大的收益，这种协调行为就是合作［11］。不同主体任务间进度协调正是这种合作行为。假设某工程由N家施工分包商共同承包，用集合N={1，2，...，n}表示。各分包商是完全独立的利益主体，按合作博弈理论，每家分包商被看作一个局中人，参与进度协调的所有分包商就构成一个进度协调联盟S⊆N。构造一个描述进度协调联盟所产生收益的特征函数V，即要对进度协调联盟S⊆N确定其进度收益V(S)。一般局中人联盟，表现为收益的增加，研究如何分配联盟后的收益。对于工程施工过程中的分包商来说，分别与业主或者总承包商签订总价合同，总的收入一定。工程进度协调的收益主要表现为任务节约的施工成本，进而获得更多的利润。其进度协调的补偿策略和收益分析在前文已经给出，因此，我们将进度协调收益定义为节约的施工成本。

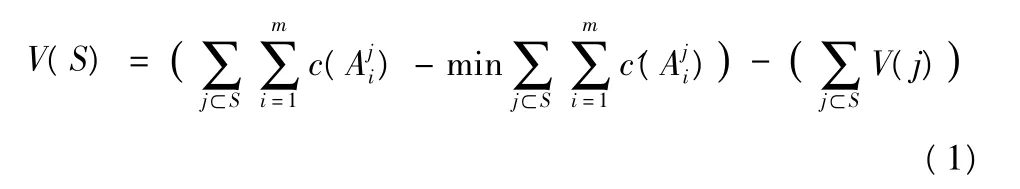
表示任务Ai属于分包商Subj。

c()为任务间不进行协调，任务Aji的施工成本。其含义是出现意外事件时总是加速赶工保证按时完工，其成本构成主要包括正常的直接成本、间接成本、自身的压缩成本。

c＇()为任务间进行协调，任务Aji的施工成本。对被协调任务而言，其含义是出现意外事件时，可以选择延长自身任务工期并支付补偿的策略进行任务间的协调，其成本构成主要包括正常的直接成本、间接成本、补偿给协调任务的压缩费用。对协调任务而言，由于得到来自被协调任务的压缩成本补偿，其成本保持不变，主要包括正常的直接成本、间接成本。

V(j)的解释:前面分析指出，任务间的协调分为两种:同一分包商主体的任务间协调;不同分包商主体的任务间协调。即使分包商彼此间不参与进度协调，同一分包商的任务间也存在这种协调关系，其收益V(j)为对在其自身的任务之间采取TCTP优化所节约的成本。由于这些任务属于同一利益主体，不存在对协作任务的补偿问题，也不需要对协调收益进行分配，故合作博弈的收益特征函数中将这一部分减去。

显然，如果各分包商之间彼此不进行进度协调，则进度协调只能在单一主体任务内进行。加入进度协调的分包商越多，任务间彼此进度协调的空间也越大，节约成本的潜力也越大，当所有的分包商的所有任务在不违反任务的合同工期下都参与进度的协调，能够达到整体收益的最大化。

模型的计算:任务的施工成本的计算以上述四类成本为基础，类似TCTP优化问题中的成本计算，这里不再叙述。由于模型建立在TCTP分析基础之上，人们对TCTP问题已有很好的研究成果，费用和协调收益的计算比较方便、明确。通过观察收集并估算对方关于任务的成本，便可大致算出各任务协调的收益。

(二)工程进度协调收益的Shapley值分配

在合作博弈理论中，有多种利益分配规则，每种分配方法都称为合作博弈的一种解概念，其中的Shapley值分配方法被广泛应用于实际，其合作博弈的解是对任何一个合作博弈都给出一个n维向量φ(V)=(φ1(V)， φ2(V)，...，φn(V)) 的一种规则，这个n维向量的分量表示相应局中人的利益分配量。并按照如下计算规则确定这个n维向量的每个分量:

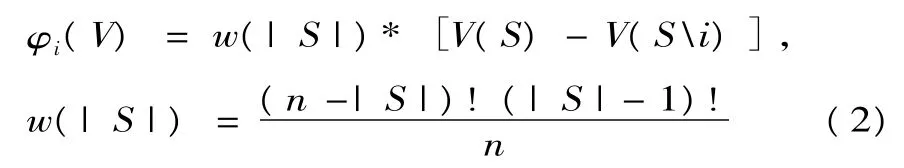
其中:|S|表示联盟S中的分包商个数;φi(V)表示局中人i在合作博弈中的分配值;Si表示成员i不参加联盟S。

在进度协调的合作博弈中，按公式(1)计算出对任何进度协调联盟S的特征函数值V(S)后，再按公式(2)计算出每个参与进度协调的分包商分配的利益。这种按照Shapley值法的收益分配方法具有这样的特征:其一，体现个体理性，即每个分包商加入进度后分得的收益不少于它不参加进度协调而独立施工时的收益;同时，任何分包商在任何子联盟中不会比在全联盟得到更大利益。其二，各个分包商在进度协调合作中的地位是平等的，依据其对进度协调的贡献大小分配收益，任何分包商分得的收益，是它在所有可能的进度协调子联盟中边际贡献的均值，当它在各子联盟中的贡献越大时，分得的收益也越大。上述这些特点体现了分配机制的公平公正，避免了“搭便车”、“平均主义”，促进了分包商在项目施工过程中进度协调的积极性，保证了分包商积极进行进度协调。

(三)计算示例

某轨道工程施工由三家分包商承担，他们分别与轨道管理公司签订施工合同，分包商是完全独立的利益主体。在施工过程中，遇见各种意外事件导致进度冲突时，彼此自主协商协调。各项任务的施工费用由上述四类成本要素计算得到，因各种情况下的计算比较烦琐，且受篇幅的限制，文中省略了分包商各种进度协调组合情况下施工费用的计算过程而直接给出这些数据。表1列出了分包商1、2、3在各种进度协调组合情况下的施工费用和进度协调收益。

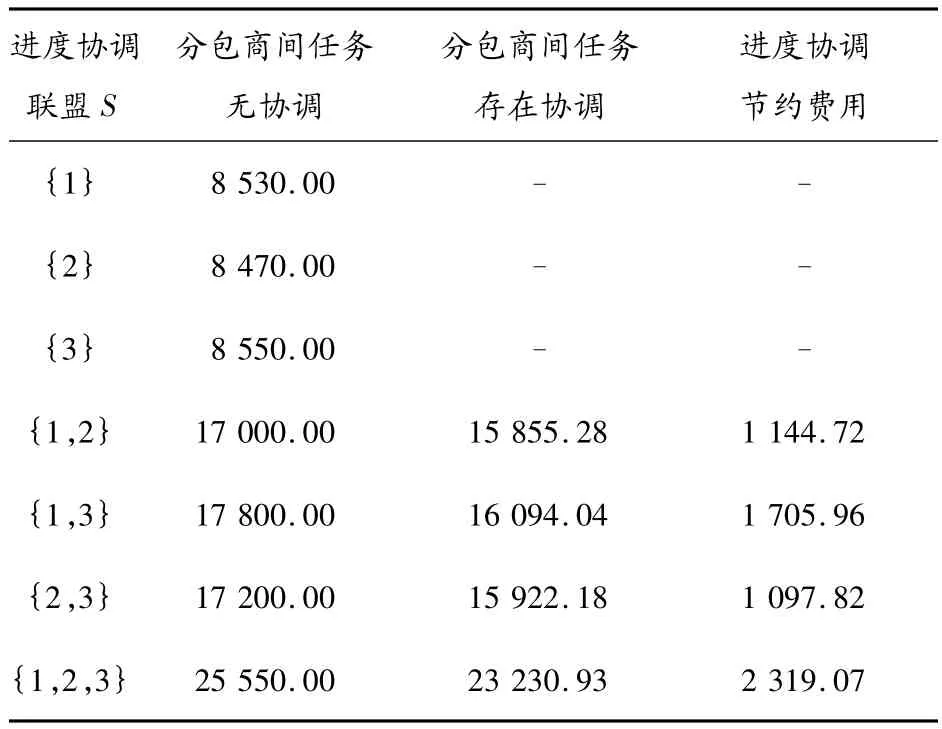
表1 各分包商进度协调组合及协调收益(万元)

用V(S)等表示进度协调联盟S进度协调(进行类似TCTP的优化)时比S内各分包商独立施工(仅仅在分包商自身任务间进行TCTP优化)所节省的费用，如用V({j，l})表示j与l进度协调共同节约的费用。根据表1数据可以得出:

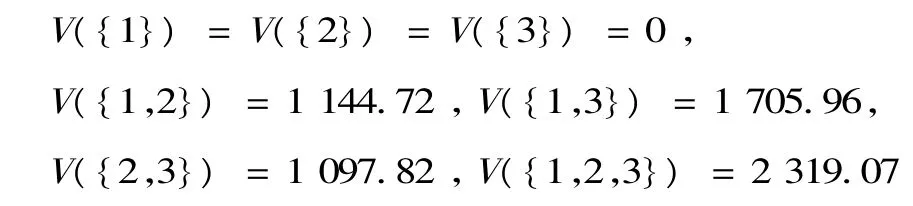
利用Shapley值法计算三家分包商分配得到的进度协调收益:

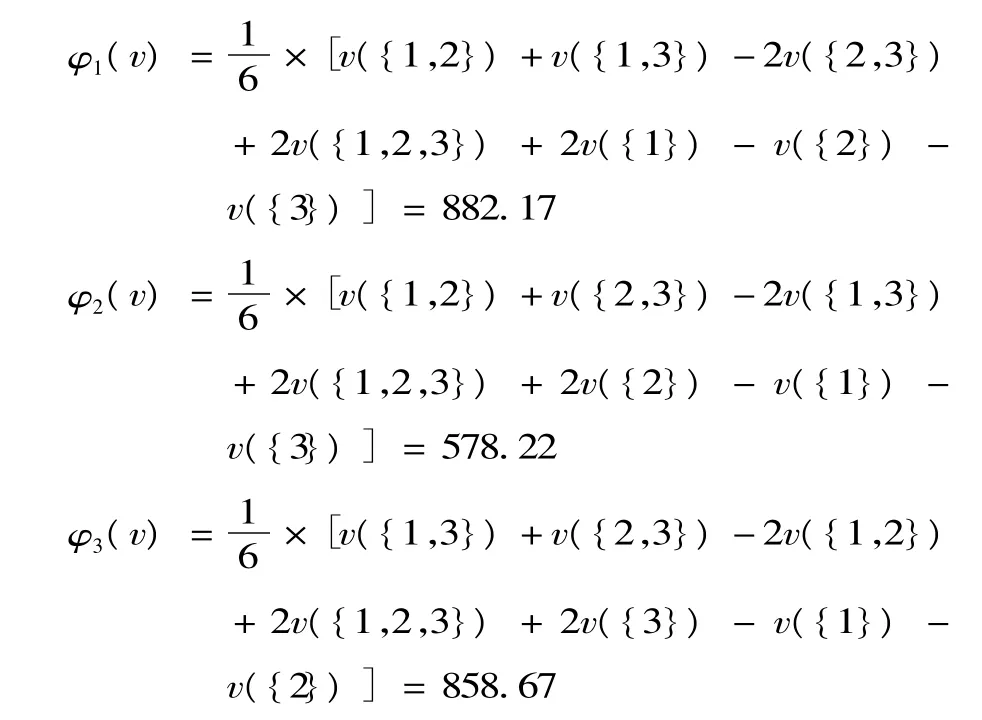
该示例的计算结果表明，通过三家施工分包商之间的工程进度协调，可提高全体施工分包商的收益，即V({1，2，3}) ≥V({1})+V({2})+V({3})，各施工分包商都有积极性加入工程进度协调，保证了进度协调联盟的稳定性，有利于分包商之间合作氛围的建立。

四、结语

基本思路:突破由监理/总承包商进行进度协调的传统模式，通过利益补偿与合理的收益分配机制，促进各分包商积极地加入自主协调，最大限度地降低施工成本，克服监理/总承包商协调存在的弊端。

笔者的研究对于有效促进工程施工中各分包商的充分合作，构建合作伙伴关系，特别是联合施工，最大限度提高经济效益具有积极意义。同时，笔者提出的利益补偿策略以及合作博弈模型也可以构成分包商进度协调的分布式决策框架，对于构建分布式调度决策支持系统具有实际借鉴意义。

［1］AL－HAMMAD A－M.Common interface problems among various construction parties［J］.Journal Perform Construction Facility，2000，14(2):71 －74.

［2］王瑞良.建设项目进度控制［M］.北京:中国水利水电出版社，1999.

［3］周辉，张玉清.谈工程建设监理的组织协调作用［J］.基建优化，2001，22(5):12 －14.

［4］常燕，卢汝生，王孟钧.我国工程总承包模式的博弈分析［J］.建筑经济，2006(9):40 －43.

［5］王先甲，曹生荣.基于合作对策的工程进度协调研究［J］.武汉大学学报(工学版)，2005，38(5):1－5.

［6］TSERNG H P，LIN W Y.Developing an electronic acquisition model for project scheduling using XML－based information standard［J］.Automation In Construction，2003，12(1):67－95.

［7］O’BRIEN W，FISCHER M A，JUCKER J V.An economic view of project coordination［J］.Construction Management and Economics，1995，13(5):393 －400.

［8］张静文，徐渝，何正文，柴国荣.项目调度中的时间—费用权衡问题研究综述［J］.管理工程学报，2007，21(1):92－97.

［9］曹小琳，汪金根.工程项目工期—资源优化方法研究［J］.土木建筑与环境工程，2000，22(2):49－54.

［10］汪嘉昱，孙永广，吴宗鑫.收益激励的优化与最优工期的选择［J］.系统工程，2000，18(3):5－11.

［11］张维迎.博弈论与信息经济学［M］.上海:上海人民出版社，1997.

Coordination of Construction Process Based on Compensation Mechanism and Shapley Value Benefit Sharing

ZHONG Bo-taoa，DING Lie-yuna，b，YU Ming-huia，ZHOU Yingb
(a.Inst.of Systems Engineering;b.School of Civil Engineering and Mechanics，HUST，Wuhan 430074，P.R.China)

The paper points out the shortcomings of centralized coordination of project construction process and provides another viewpoint:self-organize negotiation coordination.Dividing the construction process coordination into two kinds basing on TCTP:coordination between activities of the same subcontractor，coordination between activities of different subcontractors， considering the self-interesting and independency of subcontractors，the authors introduce the compensation mechanism and give a mathematical model for coordination of project construction process based on cooperative game theory.The Shapley value method is applied to the cooperative benefit sharing among the cooperation subcontractors.

process coordination;TCTP;compensation mechanism;cooperative game;Shapley value method

F283

A

1008-5831(2011)06-0074-05

2010－09－13

“数字轨道交通工程”集成建设关键技术研究(EK050348)

钟波涛(1978－)，男，华中科技大学系统工程研究所博士，主要从事工程项目协调、决策支持研究。

(责任编辑 傅旭东)