半线性抛物问题基于应力佳点的一类二次有限体积元方法
王 星,王同科
(天津师范大学 数学科学学院,天津 300387)
半线性抛物问题基于应力佳点的一类二次有限体积元方法
王 星,王同科
(天津师范大学 数学科学学院,天津 300387)
针对半线性抛物混合初边值问题,给出了一种基于应力佳点的二次有限体积元格式,并证明了格式的收敛性.具体算例表明该格式计算效果良好.
半线性抛物方程;应力佳点;二次有限体积元格式;误差估计
有限体积元方法通过离散微分方程的积分守恒形式导出计算格式,该方法既保持了差分法的简单性,又具有有限元法的精确性,已被广泛应用于科学工程计算中.在国内,该方法称为广义差分方法,早期的研究结果包含在李荣华教授的专著中[1].
有限体积元方法是基于函数插值的数值方法,对于r次Lagrange插值而言,其导函数通常具有r阶收敛精度,但不排除在插值区间的个别点上导数具有更高的收敛精度,这些点在力学中称为应力佳点.最近,王同科等[2-4]提出了基于应力佳点的高次有限体积元方法,与此同时,于长华等[5]也注意到了这一现象,并针对两点边值问题得到了一类在应力佳点处具有导数超收敛性的有限体积元方法,高广花等[3]针对一维线性抛物方程给出了基于三次插值的有限体积元方法.本研究基于文献[2-3]中的有限体积元格式的构造思想,考虑半线性抛物方程基于二次插值应力佳点的有限体积元格式,并给出了格式的收敛性分析.
1 二次有限体积元格式
考虑一维半线性抛物方程的初边值问题


2 误差分析


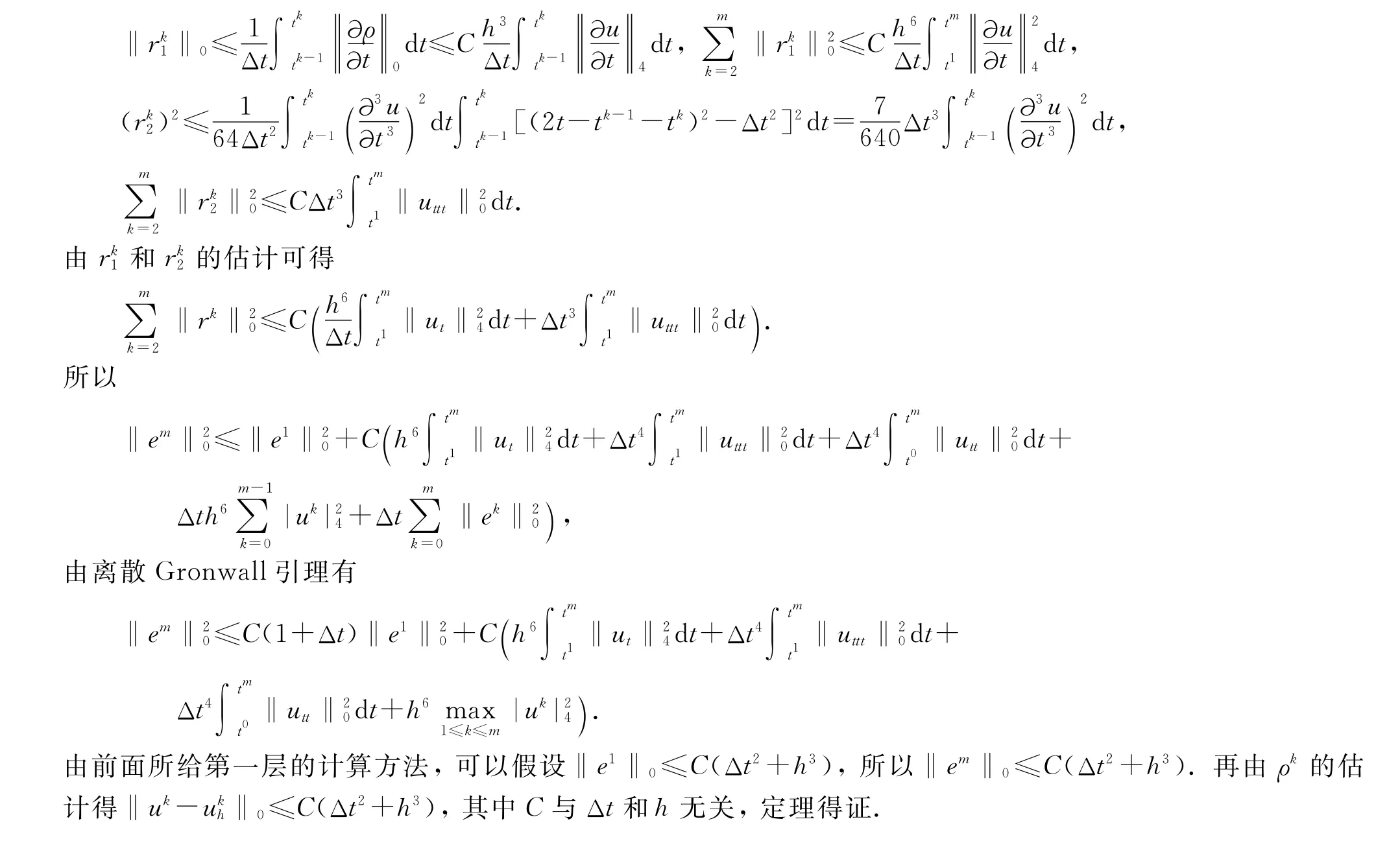
3 数值实验


表1 算例中不同步长下所得数值计算结果Table 1 Numerical calculation results of the example with different step lengths
由表1可知,节点处计算解达到了四阶精度,应力佳点处导数可达三阶精度,表明该格式计算效果良好.
[1] Li R H,Chen Z Y,Wu W.Generalized Difference Methods for Differential Equations:Numerical Analysis of Finite Volume Methods[M].New York:Marcel Dekker,2000.
[2] 郭伟利,王同科.两点边值问题基于应力佳点的一类二次有限体积元方法[J].应用数学,2008,21(4):748-756.
[3] Gao G H,Wang T K.Cubic superconvergent finite volume element method for one-dimensional elliptic and parabolic equations[J].Journal of Computational and Applied Mathematics,2010,233:2285-2301.
[4] 高广花,王同科.两点边值问题基于三次样条插值的高精度有限体积元方法[J].山东大学学报:理学版,2009,44(2):45-51.
[5] 于长华,李永海.解两点边值问题的基于应力佳点的二次有限体积元法[J].吉林大学学报:理学版,2009,47(4):639-648.
Quadratic finite volume element method based on optimal stress points for semilinear parabolic equations
WANGXing,WANGTongke
(College of Mathematical Science,Tianjin Normal University,Tianjin 300387,China)
A kind of quadratic finite volume element method based on optimal stress points is presented for semilinear parabolic equations with mixed initial boundary conditions.It is proved that the method is convergent.A numerical example illustrates the effectiveness of the scheme.
semilinear parabolic equations;optimal stress points;quadratic finite volume element method;error estimate
O241.82
A
1671-1114(2011)01-0001-05
2010-03-16
王 星(1986—),女,硕士研究生.
王同科(1965—),男,教授,博士,主要从事偏微分方程数值解方面的研究.
(责任编校 马新光)

