一种多传感器数据信息的融合算法

陈湘萍，刘南平，蔡 举

（1.贵州大学 电气工程学院，贵州 贵阳 550003；2.天津师范大学 物理与电子信息学院，天津 300387；

3.河北工业大学 信息工程学院，天津 300401）

一种多传感器数据信息的融合算法

陈湘萍1，刘南平2，蔡 举3

（1.贵州大学 电气工程学院，贵州 贵阳 550003；2.天津师范大学 物理与电子信息学院，天津 300387；

3.河北工业大学 信息工程学院，天津 300401）

为解决在多传感器信息融合技术中出现的测量维数和置信度较低、系统的探测能力和生存能力较差以及空间和时间的范围较窄等问题，提出了一种改进的PSO算法.该算法主要包括对传感器自身特点的分析，以及建立一个综合传感器信息增量和处理时间的目标函数的过程.从实验仿真结果可以看出，该算法可以有效地剔除性能不符合系统标准的传感器，从而更加有效、准确地进行数据融合.

多传感器；数据融合；PSO算法

传感器是一种检测装置，能感受到被测量的信息，并能将检测感受到的信息按一定规律变换成为电信号或其他所需形式的信息输出，以满足信息的传输、处理、存储、显示、记录和控制等要求.多传感器 信 息 融 合 （Multi－Sensor Imformation Fusion，MSIF）［1－3］是指对传感器的数据进行多级别、多方面、多层次的处理，从而产生新的有意义的信息，而这种新信息是任何单一传感器所无法获得的.多传感器信息融合由美国国防部在20世纪70年代提出，近30多年来，随着信息融合技术得到了巨大的发展，包括我国在内的许多国家都将它列为重点发展的关键技术.

实现多传感器信息融合的关键技术是选择最优的传感器或传感器组，从而减少目标环境的不确定性，这种不确定性可以用基于信息论的方法度量.目前，主要方法包括：Hintz和Mc Intyre等将信息论中的熵用于调度单传感器对多目标的跟踪［4］；Manyika和Durrant－Whyte对数据融合和传感器管理建立了概率信息模型［5］，给出了不同情况下的数据融合方式；Pierre Dodin等以 Kull－back－Leibler熵作为目标函数，对目标和传感器进行有效配对，通过不同仿真证明了方法的有效性.

虽然传统寻优方法在理论上能够得到最优解，但受到问题维数的制约很难满足实际要求，PSO（Particle Swarm Optimization）算法是近期提出的一种全新的全局优化算法，在求解多维数、非线性和不可微的复杂问题上具有良好表现，因其程序实现简洁，需调整参数少，而发展迅速.本研究运用全局搜索能力更强的改进PSO算法——QD－PSO［5－7］处理由时间组成的目标函数，并进行寻优，以实现传感器组的管理.实验证明：该算法潜在的并行性和分布性为处理海量数据提供了技术保证，在传感器管理中具有良好的应用前景.

1 算法原理

1.1 多传感器信息融合算法

现代融合算法是根据人工智能理论和现代信息论等发展起来的一类融合算法，常用的算法主要有聚类分析（Cluster Analysis）、模糊逻辑（Fuzzy Logic）、神经网络（Neural Networks）、小波理论（Wavelet Theory）、粗糙集理论（Rough Set Theo－ry）、支持向量机（Support Vector Machines）和PSO算法等方法，表1是部分信息融合算法的相关信息.

表1 信息融合算法Table1 Data fusion algorithm

融合结构若从信息输入和输出的角度进行划分，可以统称为数据特征决策模型，通常分为5类.属性级数据融合结构和DFD（Data Feature Decision）结构的关系如图1所示.

图1 属性级数据融合结构和DFD结构关系Figure 1 Relation between class attribute data fusion and DFD structure

1.2 标准PSO算法

粒子群优化算法是近10年提出的一种全局优化算法，其数学公式可表示为：

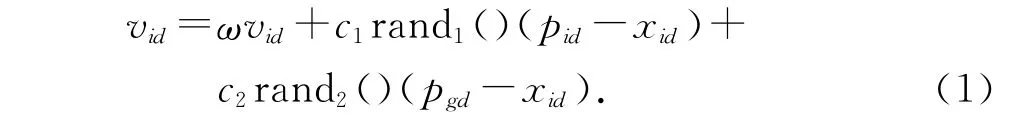
其中，x id是粒子当前的位置向量，vid是粒子的运动速度向量，p id为粒子个体位置最优值，p gd为群体最优值，即群体中所有粒子在所有搜索过的解空间中适应度最高的向量，i＝1，2，…，m表示群落由m个粒子组成，g表示群体中个体位置最优值的个数，d＝1，2，…，D表示d维空间，ω是惯性权重，c1和c2是非负的学习常数，rand1（）和rand2（）是介于［0，1］之间的随机数.

1.3 QD－PSO算法

由于标准PSO存在缺陷，因此，可以根据粒子群的基本性质，运用具有全局收敛的QD－PSO算法来降低这一问题发生的概率，具体数学过程如下.首先，进行粒子状态更新操作：

1.4 基于QD－PSO算法的总体流程

步骤1：初始化.确定QD－PSO算法的各项参数，在搜索范围内随机初始化x id v id，其中粒子的维数d即为待选择传感器的数目N.

步骤2：计算各传感器被使用的概率，按目标函数式计算每个粒子的适应值.

步骤3：将每个粒子的适应值与其经历过的最好值进行比较，如果更好，则将其作为当前粒子的个体最优值.

步骤4：将每个粒子的个体最优值与群体最优值进行比较，如果更好，则将其作为群体最优值.

步骤5：更新每个粒子的速度和位置.

步骤6：若未达到终止条件，则转步骤2.

2 仿真实例

应用8个传感器来区分目标的类型，设目标有2种可能的情况：A1＝敌方航母，A2＝我方航母.

对传感器A1和A2进行事件监测，并根据式（1）计算得到传感器模糊信息属性，即参数性能，如表2所示.

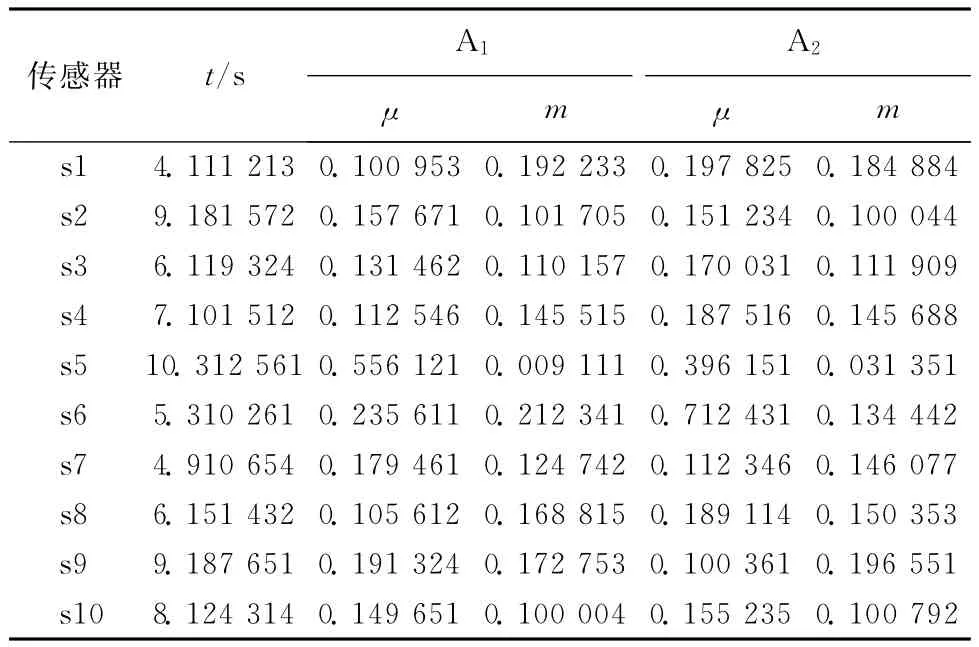
表2 传感器参数性能表Table 2 Sensor parameters

表2中，t代表时间，μ代表10个传感器检测A1和A2的隶属度，m代表传感器模糊信息增量.

选择种群大小为150，令c1＝c2＝12，Vmax＝2 000，根据QD－PSO算法的流程更新微粒的航行速度和位置，并按照系统的不同要求选择不同的传感器组.当传感器处理时间是重要的参数时，设其权重为ω1∶ω2＝1∶10，则所选传感器组实验结果如表3所示.

表3 ω1∶ω2＝1∶10时，所选传感器组实验结果Table 3 Experimental result whenω1∶ω2＝1∶10

当传感器信息增量比较重要时，设其权重为ω1∶ω2＝10∶1，所选传感器组试验结果如表4所示.

表4 ω1∶ω2＝10∶1时，所选传感器组实验结果Table 4 Experimental result whenω1∶ω2＝10∶1

当传感器信息增量和处理时间同等重要时，设其权重为ω1∶ω2＝1∶1，所选传感器组如表5所示.

表5 ω1∶ω2＝1∶1，所选传感器组实验结果3Table 5 Experimental result whenω1∶ω2＝1∶1

通过以上实验对比可以看出，根据设置权重的不同，所选择的传感器组也不尽相同，从而使系统的性能达到要求.由此可见，通过QD－PSO算法可以有效地剔出信息增量小且处理时间长的传感器.

3 结论

多传感器信息融合算法技术在信息融合中的地位越来越重要，基于QD－PSO的传感器优化方法可以使信息融合更准确地执行，使融合在信息源的可靠性、信息的冗余度和互补性以及进行融合的分级结构不确定的情况下，以近似最优的方式对传感器数据进行融合.

［1］ 应宁，陆大金.多传感器数据融合模型评述［J］.清华大学学报：自然科学版，1996，36（9）：14－20.

［2］ 王欣.多传感器数据融合算法研究［D］.西安：西安电子科技大学，2008：19－32.

［3］ 何友，王国宏，陆大绘，等.多传感器信息融合及应用［M］.北京：电子工业出版社，2000：19－25.

［4］ Hintz K J，McIntyre G A.Goal lattices for sensor management［C］／／Russian Communication Engineers.Communication System.System on Applications of Sensor Data Fusion，University of Southern California，Los Angeles，California.New York：SPIE Proceedings，1999：249－255.

［5］ Manyika J M，Durrant－Whyte H F.Data Fusion and Sensor Management：a Decentralized Information－theoretic Approach［M］.New York：Ellis Horwood，1994：25－30.

［6］ Bergh V D，Engelbrecht A P.Cooperative learning in neural networks using particle swarm optimizers［J］.South Africa Computer Journal，2000，26（5）：84－90.

［7］ David L H，Llinas J.An introduction to multisensor date fusion［C］／／Proceedings on multisensor date fusion.Analysis of the multi－sensor－multi－target tracking resource allocation problem，MIT，Boston，Massachusetts.Toronto：Proceedings of the IEEE，1997：6－23.

［8］ Leung H，Hu Z，Blanchette M.Evaluation of multiple target track initiation techniques in real radar tracking environment［J］.Radar，Sonar and Navigation，1996，143（4）：246－254.

Data fusion algorithm based on multiply sensors

CHENXiangping1，LIUNanping2，CAIJu3

（1.The Electrical Engineering College，Guizhou University，Guiyang 550003，Guizhou Province，China；
2.College of Physics and Electronic Information，Tianjin Normal University，Tianjin 300387，China；
3.School of Information Engineering，Hebei University of Technology，Tianjin 300401，China）

In order to solve the problems of low measurement dimensions and confidence，bad behavior of detection capability and survivability of the system，narrower range of space and time which appear in multi－sensor information fusion，an improved PSO algorithm has been proposed.The analysis of own characteristics of the sensor，and the establishment of an integrated sensor information gain and processing time of the objective function are included.The simulation results show that the sensors which do not meet the standard of system can be effectively eliminated so that more effective and accurate data fusion can be carried out.

multiply sensors；data fusion；PSO algorithm

TP18

A

1671－1114（2011）01－0042－03

2010－05－23

陈湘萍（1965—），女，高级工程师，主要从事计算机测控技术方面的研究.

刘南平（1971—），男，副教授，主要从事智能信息处理方面的研究.

（责任编校 纪翠荣）