太湖遥感反射率变化特征及其影响因素分析
钱昊钟,赵巧华,何金海,孙德勇,姜雨薇,陶蓉茵
太湖遥感反射率变化特征及其影响因素分析
钱昊钟1,赵巧华2,何金海1,孙德勇2,姜雨薇2,陶蓉茵2
(1.南京信息工程大学大气科学学院,南京 210044;2.南京信息工程大学遥感学院,南京 210044)
基于2010年10月4—8日在太湖全湖范围32个样点的水体光学参数和理论数值模拟结果,研究了太阳天顶角θ、散射系数和吸收系数的比值b/a及表征光场分布的参数Q对太湖遥感反射率变化的影响。结果表明,遥感反射率随θ的增大而增大,且当θ较小(0°~20°)或较大(80°~89°)时,其变化对遥感反射率增幅的影响较小;当b/a增大时,遥感反射率也随之增大,二者变化趋势呈显著正相关;Q较大时(如6~7),其变化对遥感反射率增幅的影响较小;Q较小时(如2~3),其变化对遥感反射率增幅的影响明显;遥感反射率随Q的增大呈递减的趋势。
遥感反射率;散射系数;吸收系数;光场分布;太阳天顶角
0 引言
在对太湖的治理、监测和预警过程中,水环境的定量遥感监测越来越受到关注。水体的遥感反射率是水色遥感的基础物理量,也是表征水体表观光学特性的重要物理参数,可直接用于水环境的遥感监测模型。为此,对水体遥感反射率的变化及其影响因素的研究对遥感监测太湖水质参数、掌握水生态环境变化具有重要的意义。
关于遥感反射率的变化及其影响因素,国内外学者已经开展了大量的研究。黄昌春等[1]发现,遥感反射率Rrs与水面下反射率R(0-)密切相关,二者之间的关系主要由水—气界面状况和表征光场分布的参数 Q决定,在水体各向均匀的条件下,R(0-)可以由后向散射系数、吸收系数和表征光场几何结构的函数(f)来表示[2],其中f受太阳入射天顶角的影响较为明显[1];Morel等[3]则对 Q 以及 f和Q进行了理论性的探索,指出了 Q的范围在0.3 ~6.5之间;黄昌春等[4]研究了在高散射特性水体中,太阳天顶角、单次散射反照率Wo与双向性函数的关系。上述研究对与遥感反射率相关的因素进行了较好的探讨,但对遥感反射率变化影响的量化分析却较少涉及。
本文在假定太湖水质均匀的前提下,根据遥感反射率公式进行数值实验,分别研究太阳天顶角、散射系数和吸收系数的比值(b/a)以及表征光场分布的参数Q对水体遥感反射率的影响,并基于2010年10月4日—10月8日覆盖全太湖的32个点位的水体实测光谱数据和水质分析数据对数值实验结果进行了验证。
1 研究区与数据获取
1.1 研究区及采样点分布
太湖位于长江下游地区,是我国第三大淡水湖,面积约2 338 km2。太湖对周边地区的经济发展具有重要的作用[5]。近年来,随着太湖周边城市经济的高速发展,工农业和生活污水被大量排入太湖,太湖水体生态环境不断恶化,蓝藻水华频发,不仅破坏了水体景观,还严重制约了周围城市的可持续发展[6-7]。
2010年10月4—8日期间,对太湖全湖32个采样点进行了数据采集(采样点分布见图1),数据采集时间为每天7:30~16:00。光谱数据测量时天气晴朗,天空少云,平均风速为2 m·s-1左右,水面基本平静。
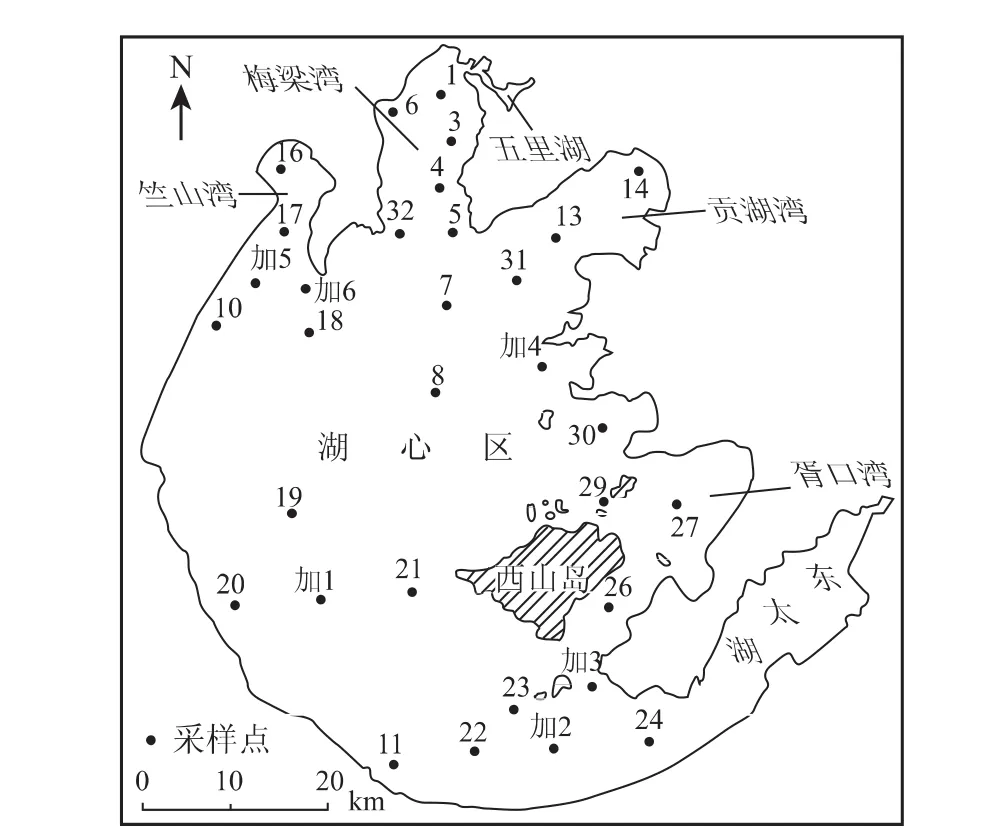
图1 采样点分布图Fig.1 Location of sampling stations
1.2 总悬浮物光谱吸收系数测定
总悬浮颗粒物的吸收系数利用定量滤膜技术(QFT)测定[8]。先用滤膜过滤一定量的水样,然后用UV-240 IPC型紫外分光光度计测量过滤后的滤膜的吸光度,最后用吸光度计算吸收系数。
吸光度的计算公式[9]为
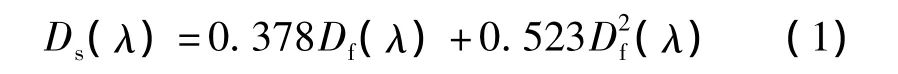
式中,Ds(λ)为校正后滤膜上悬浮颗粒物的吸光度;Df(λ)为直接在仪器上测定的滤膜上颗粒物的吸光度减去700 nm波长处的吸光度的差。
光谱吸收系数的计算公式为

式中,ap(λ)为光谱吸收系数;A为沉积在滤膜上的颗粒物的有效面积;V为被过滤水样的体积。
1.3 有色可溶性有机物光谱吸收系数测定
先用0.22 μm的滤膜过滤水样,提取出黄质;然后将黄质水样放入1 cm×4 cm的比色皿中,再利用分光光度计(实测范围240~800 nm)测量有色可溶性有机物(CDOM)的吸光度。光谱吸收系数的计算方法为:先利用公式[10]
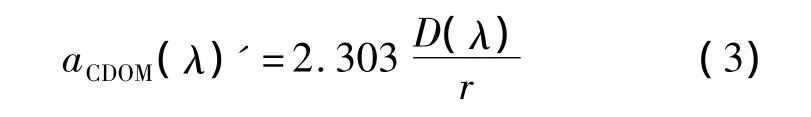
计算各波长的吸收系数,再利用公式
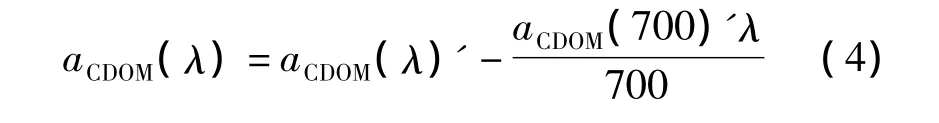
进行散射校正。
式中,D(λ)为吸光度;r为光程路径(m);aCDOM(λ)'为波长λ的未校正的吸收系数(m-1);aCDOM(λ)为波长λ的吸收系数(m-1);aCDOM(700)'为参考波段700 nm处的吸收系数。
1.4 上行辐亮度和上行辐照度测量与计算
表观光学参数的测定与水样采集同步进行。使用德国Trios公司生产的SAM-8099光谱辐射仪(采样波长范围为320~950 nm)采集上行辐照度和上行辐亮度数据。观测时,从水表0 m处起,垂直往下每隔10 cm采集一次数据,共13个深度。为了消除水体表面波对水下光场的影响,本文采用赵巧华等[11]的方法,根据实测数据拟合水体中各层的平均上行辐照度与上行辐亮度。
2 遥感反射率反演
2.1 遥感反射率测量与计算
水面以上反射率光谱数据的采集和处理方法参见文献[12]。使用美国ASD公司生产的FieldSpec3系列野外便携式地物波谱仪(该仪器可用于实时观察并测量反射率、透射率和辐照度,波谱测量范围为350~2 500 nm)进行水面光谱测定。采集数据时,用撑杆将仪器伸出船沿1 m左右,以尽量减少船体阴影的影响。仪器观测平面与太阳入射平面的夹角φ要求满足90°<φ<145°,仪器与湖面法线方向夹角θ要求满足30°<θ<45°,以避免大部分直射和反射的太阳光[13]。在仪器面向水体进行测量后,将仪器在观测平面内向上旋转一个角度,使天空光辐亮度Lsky观测方向的天顶角等于测量时的观测角。由光谱仪实测数据提取离水辐亮度和遥感反射率(Rrs),其算法[13-14]为
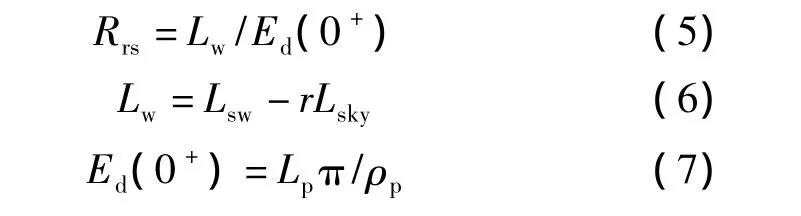
式中,Lw为水体辐亮度(W·m-2·nm-1·sr-1);Lsw为总的水体辐亮度(W·m-2·nm-1·sr-1);Lsky为天空漫反射光(W·m-2·nm-1·sr-1);Lp为标准灰板测量值(W·m-2·nm-1·sr-1);Ed(0+)为水体表面入射总辐照度;r为气—水界面反射比,平静水面取r=2.2%;ρp为标准灰板的反射比(%),实际测量时采用30%的标准板。
在每个采样点,对于每个参量,仪器自动采集10~20条光谱曲线数据。先对测得的光谱数据进行异常数据剔除,去除明显异常的光谱曲线,再对剩下的光谱数据取平均值,最后将平均处理后的数据代入式中计算得到实测的遥感反射率。
2.2 遥感反射率推演
利用蒙特-卡罗模型推导出用后向散射系数和吸收系数来表示水面下反射率R(0-)的公式[15],
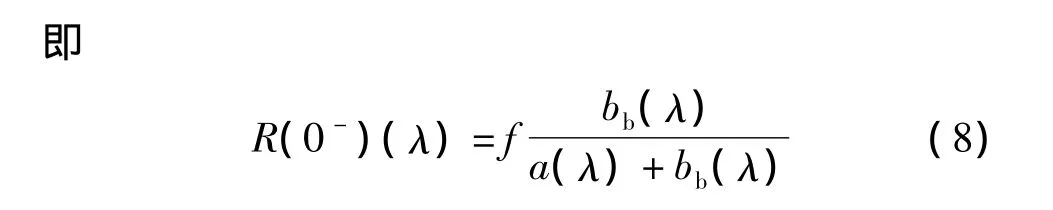
式中,bb(λ)为总的后向散射系数;a(λ)为吸收系数;f=0.975 - 0.629μ0[16](μ0为水面下入射直射太阳光的折射角余弦值,根据采样点的具体时间和纬度以及当地赤纬即可计算出各个采样点的太阳高度角,从而进一步计算出μ0)。
遥感反射率Rrs与水面下反射率R(0-)关系密切,它们之间的关系可由如下公式得到,即
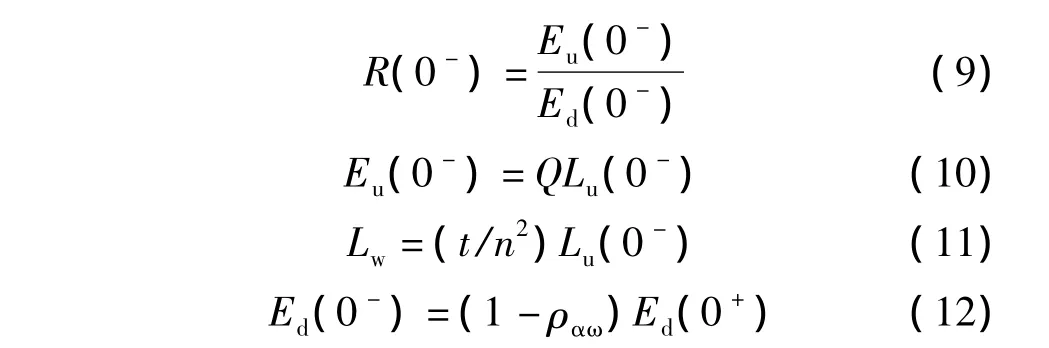
由式(9)~(12)推算得到
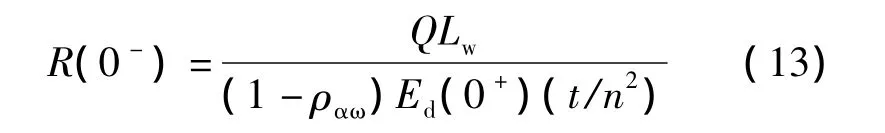
将式(13)代入式(5),得

式(9)~(14)中,Eu(0-)为表层水面下方的上行辐照度;Ed(0-)为表层水面下方的下行辐照度;Lu(0-)为表层水面下方的上行辐亮度;ραω为气—水表面辐照度反射率,ραω在 0.04 ~0.06 之间,在此取 ραω=0.05[17];n 为水体的折射指数,通常取值为1.34;t为气—水界面的菲涅耳透射系数,通常取值为 0.98,一般情况下 t/n2取值为 0.54[18];a 为吸收系数;b为散射系数;bb为总的后向散射系数,本文采用 Petzold[19]的测量结果,即 bb=0.019 b;Q 为光场分布参数,受不同的水体、太阳角度的影响而不同。上述参数代入式(14)可得

3 结果与分析
3.1 太湖水体实测固有光学参数的变化特征
各个测点的吸收系数、散射系数随波长的变化与介质的选择性吸收及其散射的特征有关。如图2(a)、(b)所示,吸收系数和散射系数在波长较短时的值比较大,波长较长时的值较小。相比较而言,散射系数呈现出的单调递减趋势较为明显,但递减速度并不突出,而吸收系数的变化则较为剧烈。从图2(c)来看,散射系数(b)和吸收系数(a)的比值(b/a)表现出如下几个特征:①在400~500 nm范围内,散射和吸收系数的比值相对较小,主要原因是在该谱段悬浮颗粒物和黄质在短波段有强烈的吸收作用;②非藻类颗粒物和黄质吸收系数随波长递减,而散射系数衰减相对较慢,以致在550~580 nm范围内出现明显的波峰;③在624 nm和670 nm附近均存在波谷,主要是由于藻蓝素在624nm处和叶绿素a在676 nm处有相对较强的吸收所致;④在700 nm附近,水体和叶绿素a的吸收系数最小,因此出现了明显的波峰[20-21]。
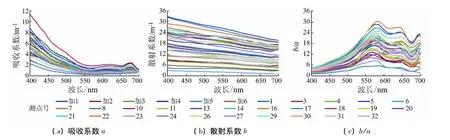
图2 太湖32个测点吸收系数、散射系数及其比值Fig.2 Spectral characteristics of absorption coefficient,scattering coefficient and ratio of them of the 32 measure points in Taihu Lake
表1是对太湖32个样点的吸收系数(a)和散射系数(b)及其比值(b/a)做出的统计。各谱段的吸收系数平均值中最大的出现在400 nm处,该处吸收系数的变化范围为2.31~11.28/m,平均值为5.61/m;随着波长的增加吸收系数平均值逐渐降低,到580nm处,吸收系数的变化范围为0.24~1.88/m,平均值为0.78/m;在580~700 nm 谱段,随着波长的增加,吸收系数平均值先是增加,随后又降低,在680 nm处吸收系数平均值出现一个峰值,为1.14/m。散射系数平均值则呈现出随波长增加而递减的趋势。此外,各谱段的吸收系数和散射系数的标准差从短波到长波依次递减,说明各样点的吸收系数和散射系数从短波到长波逐渐趋于稳定。

表1 特殊谱段吸收系数、散射系数及其比值统计数据Tab.1 Statistical values of absorption,scattering coefficients and ratio of them
3.2 太阳天顶角变化对遥感反射率的影响
首先在Q取定值的情况下,研究太阳天顶角(θ)对遥感反射率的影响。当Q取固定值(Q=4.5[4])时,遥感反射率仅与 b/a 和 θ有关。当 θ在0°~89°间变化、b/a在0~20间变化时,遥感反射率的变化如图3(a)所示。在b/a较小时,θ的变化对遥感反射率的影响较小,特别是在b/a<2时,遥感反射率随θ增大的趋势很小,几乎可以忽略不计;随着b/a的增大,θ的影响逐渐明显,且θ越大,遥感反射率越大。
当b/a取固定值(b/a=15)时,遥感反射率仅与Q和θ有关。当θ在0°~89°间变化、Q在2~7间变化时,遥感反射率的变化如图3(b)所示,曲线走势与图3(a)相类似:当θ在0°~10°和80°~89°间变化时,遥感反射率的变化比较小;而θ在10°~80°间变化时,遥感反射率的变化比较大。Q较大(Q取5~7)时,曲线走势较为平缓。随着Q的减小,遥感反射率随θ增大而增大的趋势越来越明显。

图3 遥感反射率与太阳天顶角关系Fig.3 The relationship between remote sensing reflectance and solar zenith
总体而言,无论Q或b/a如何变化,θ越大遥感反射率越大,出现这种现象的原因在于当θ增大时,光的传输行程增长,光子散射的几率加大,发生散射的可能性也增大,使得因前向散射造成的向上传输的辐射增强,遥感反射率增大,从式(15)也可以得到证明;同理,当θ减小时,光的传输行程减短,散射系数减小,遥感反射率随着θ的减小而减小。
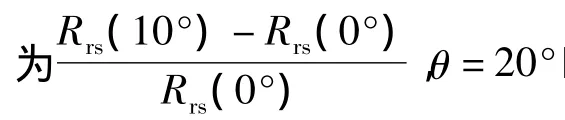

表2 太阳天顶角的变化对遥感反射率变化的影响(Q=4.5,b/a=15)Tab.2 The effect on the change of remote sensing reflectance from the change of solar zenith(Q=4.5,b/a=15)
3.3 散射系数和吸收系数比值变化对遥感反射率的影响
为简单起见,分别固定 Q(Q=4.5)和 θ(θ=60°),遥感反射率随散射系数和吸收系数比值b/a变化的趋势如图4所示。
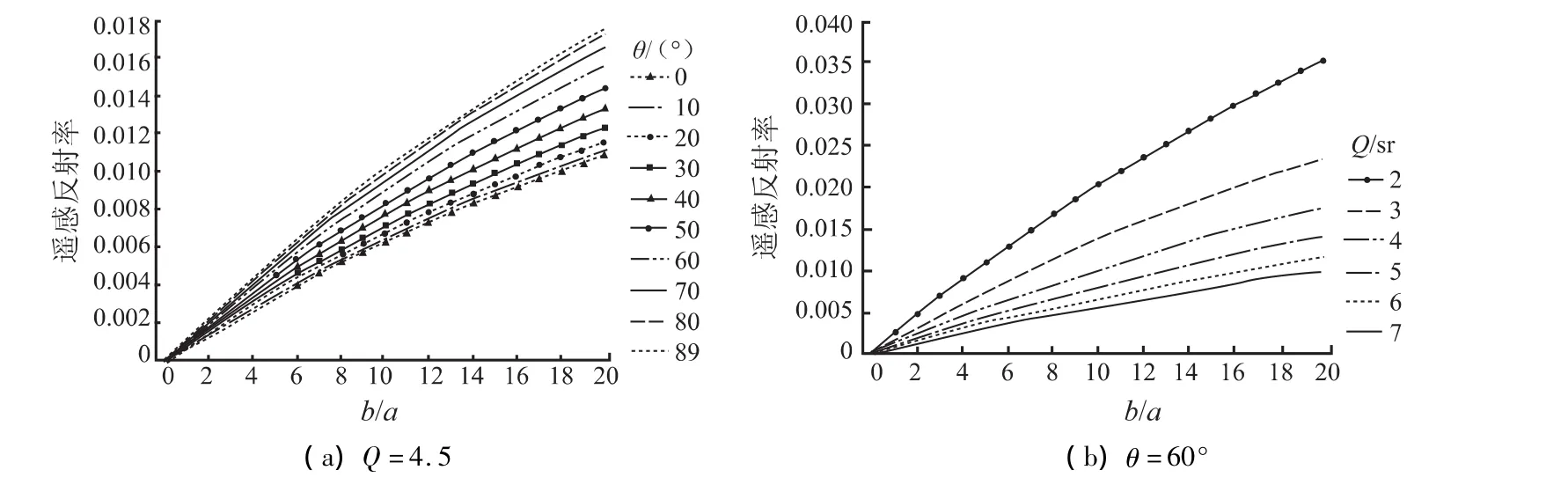
图4 散射系数和吸收系数比值对遥感反射率的影响Fig.4 The effect on the remote sensing reflectance from the change of the ratio of scattering and absorption coefficient
当 Q=4.5,θ较大(80°~89°)或较小(0°~20°)时,遥感反射率随b/a变化的曲线斜率变化较小;而θ在20°~80°间变化时,曲线斜率的变化明显;当θ取定值60°时,Q越小,遥感反射率随b/a变化的近似线性曲线的斜率变化越大。
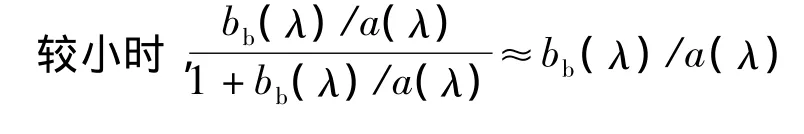
3.4 Q值变化对遥感反射率的影响
b/a取定值15、θ在0°~89°间变化时的遥感反射率随Q变化的曲线如图5(a)所示;θ取定值60°、b/a在0~20变化时,遥感反射率随Q变化的曲线如图5(b)所示。
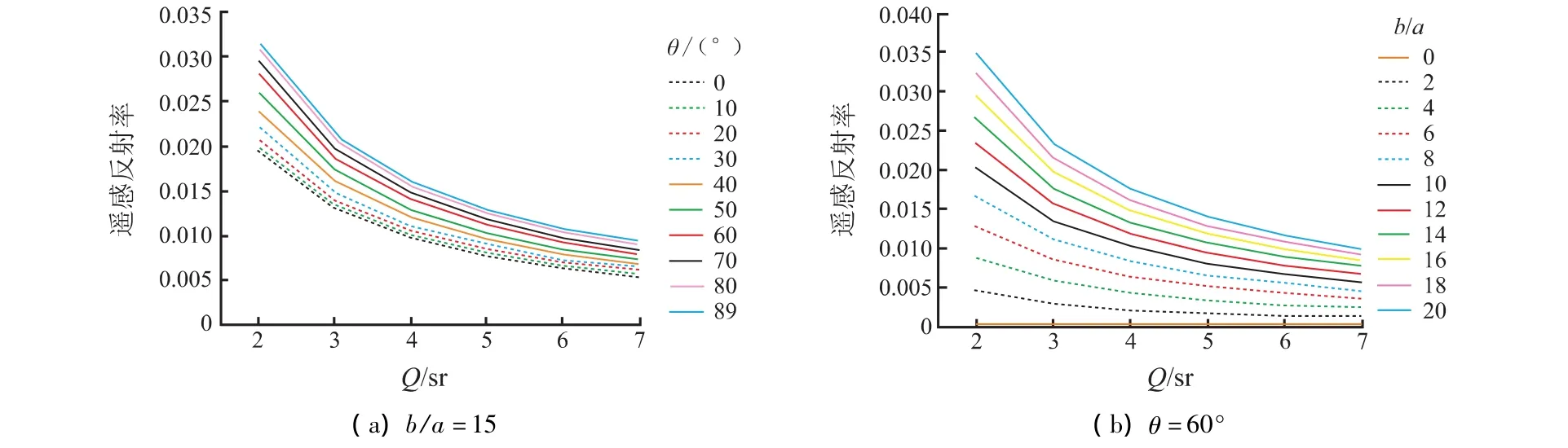
图5 Q与遥感反射率关系Fig.5 The relationship between Q and remote sensing reflectance
θ或b/a越大,遥感反射率随Q的增大而递减的趋势越明显;θ或b/a越小,遥感反射率随Q的增大而递减的趋势越不明显。特别是当b/a较小(如b/a=0,即散射为零)时,即没有在光子传输方向发生改变,也就没有向上传输的辐射,遥感反射率也就不随Q变化而变化。
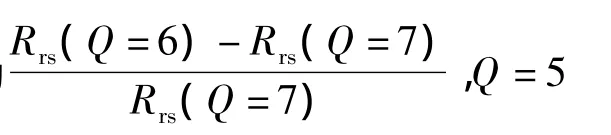

表3 Q变化对遥感反射率的影响(θ=60°,b/a=15)Tab.3 The effect on the remote sensing reflectance from the change of Q(θ =60°,b/a=15)
4 验证与讨论
4.1 验证
为了验证本文理论基础的可信度,选取具有代表性的18个采样点,对模拟的遥感反射率和用ASD实测的遥感反射率进行了比较(其中模拟的遥感反射率是通过将实测的Q、b/a与θ代入式(15)求得的)。从整体上看,模拟的和实测的遥感反射率曲线的趋势基本一致,在560 nm、650 nm和700 nm附近都有明显的波峰,在680 nm附近都出现了明显的波谷,而在620 nm附近的波谷则都较为平缓(图6)。要谱段的r值均大于rα,说明遥感反射率的模拟结果较好,基本满足本次数值研究的要求。
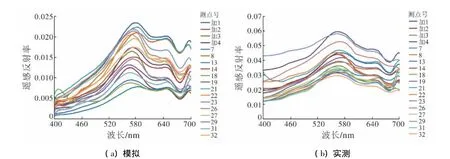
图6 模拟和实测遥感反射率Fig.6 Remote sensing reflectance simulated and measured by ASD

表4 模拟与实测遥感反射率相关关系Tab.4 The correlation between simulated and measured remote sensing reflectance
4.2 问题与讨论
实测光谱与通过遥感反射率理论模拟的光谱之间虽然相似度较高,但在数值上还是存在着一定的差异。其原因是多方面的:①本文中通过太阳高度角来获得参数f的公式是经验公式,实际上,单次反照率和风速也是影响f的重要因子[1];②后向散射概率bb/b=0.019是个经验值,一般认为,在大洋开阔水体中,后向散射概率bb/b基本稳定,可默认为0.015;但Kirk[23]认为对许多沿岸和中度混浊水体而言,0.019 比较合适;Whitlock等[24]的研究则发现浊水的后向散射概率大概为0.059;③对于Q的取值,国内外众多学者作了很多研究。唐军武等[12]认为遥感反射率的最大误差来源于Q的不确定;Morel等[3]认为 Q 的范围在 0.3 ~6.5 之间;Gons[25]则认为 Q 通常在 1.7 ~7.0 之间变化,而且水越是浑浊,Q就越接近π;黄昌春等[4]研究表明,在内陆湖泊水体中,单次散射反照率W0和太阳高度角是影响Q的主要因素;本文中实测的Q是通过公式Q=Eu(0-)/Lu(0-)获得的,其中,上行辐照度和上行辐亮度是通过实测数据拟合获得的[11],拟合本身就存在一定的误差;④在使用ASD测量光谱数据的过程中,尽管严格执行了操作规范,但仍可能有少量因波浪所致的镜面反射信号进入传感器。
5 结论
(1)当太阳天顶角增大时,光的传输行程增长,光子散射的几率加大,发生散射的可能性也增大,因此遥感反射率也增大;当天顶角减小时,光的传输行程减短,散射系数减小,因此遥感反射率随着天顶角的减小而减小。而太阳天顶角较小(0°~20°)或较大(80°~89°)时,其变化对遥感反射率变化幅度的影响比较小;天顶角在20°~80°变化时,其变化对遥感反射率变化幅度的影响比较大。
(2)散射系数和吸收系数的比值b/a越大,后向散射现象就越明显,遥感反射率也就越大;而且,遥感反射率随b/a变化而变化的趋势呈线性递增的关系。
(3)表征光场分布的参数Q较大时,其变化对遥感反射率增幅的影响较小;而Q较小时,其变化对遥感反射率增幅的影响明显;总体而言,遥感反射率随Q的增大呈递减的趋势。
[1] 黄昌春,李云梅,王 桥,等.水—气界面参数和二向性影响因素交互作用研究[J].光学学报,2010,30(3):625 -632.
[2] Gordon H R,Brown O B,Jacobs M M.Computed Relationships Between the Inherent and Apparent Optical Properties of a Flat Homogeneous Ocean[J].Applied Optics,1975,14(2):417 -427.
[3] Morel A,Gentili B.Diffuse Reflectance of Oceanic Waters II,Bi- directional Aspects[J].Applied Optics,1993,32(32):6864 -6879.
[4] 黄昌春,李云梅,孙德勇,等.Q值的影响因素分析及其参数化[J].光学学报,2009,29(8):2060 -2066.
[5] 李 军,刘丛强,王仕禄,等.太湖水体溶解营养盐(N、P、Si)的冬、夏二季变化特征及其与富营养化的关系[J].地球与环境,2005,33(1):63 -67.
[6] 高锡云,陈宇炜,蔡后建.梅梁湾及大太湖水环境现状与富营养化趋势分析[M]//蔡启铭.太湖环境生态研究(一).北京:气象出版社,1998.
[7] 朱广伟.太湖富营养化现状及原因分析[J].湖泊科学,2008,20(1):21-26.
[8] Mitchell B G.Algorithms for Determining the Absorption Coefficient for Aquatic Particulates Using the Quantitative Filter Technique(QFT)[J].Proceedings of SPIE,1990,1302:137 -148.
[9] Cleveland J S,Weidemann A D.Quantifying Absorption by Aquatic Particles:A Multiple Scattering Correction for Glass-fiber Filters[J].Limnology and Oceanography,1993,38(6):1321 -1327.
[10] Bricaud A,Morel A,Prieur L.Absorption by Dissolved Organic Matter of the Sea(Yellow Substance)in the UV and Visible Domains[J].Limnology and Oceanography,1981,26(1):43 -53.
[11]赵巧华,秦伯强,张运林.太湖梅梁湾水下光场扰动的特征分析[J].光学学报,2007,27(5):760 -765.
[12]唐军武,田国良,汪小勇,等.水体光谱测量与分析I:水面以上测量法[J].遥感学报,2004,8(1):37 -44.
[13]李铜基,唐军武,陈清莲,等.光谱仪测量离水辐射亮度的方法[J].热带海洋学报,2001,20(4):56 -60.
[14]冯 伟,冯学智,马荣华.太湖水体叶绿素浓度与反射光谱特征关系的研究[J].遥感信息,2007(1):18-21.
[15] Kirk J T O.Dependence of Relationship Between Inherent and Apparent Optical Properties of Water on Solar Altitude[J].Limnology and Oceanography,1984,29(2):350 -356.
[16] Kirk J T O.Light and Photosynthesis in Aquatic Ecosystems[M].Cambridge:Cambridge University Press,1994:45 -58.
[17] Hoogenboom H J,Dekker A G,Althuis A.Simulation of AVIRIS Sensitivity for Detecting Chlorophyll Over Coastal and Inland Waters[J].Remote Sensing of Environment,1998,65(3):333 -340.
[18]孙德勇,李云梅,乐成峰,等.应用水表面下辐照度比估测太湖夏季水体叶绿素 a浓度[J].湖泊科学,2007,19(6):744-752.
[19] Petzold T J.Volume Scattering Functions for Selected Ocean Waters[M].San Diego:Scripps Institution of Oceanography Ref,1972:72-78.
[20]李素菊,吴 倩,王学军,等.巢湖浮游植物叶绿素含量与反射光谱特征的关系[J].湖泊科学,2002,14(3):228 -234.
[21]李素菊,王学军.巢湖水体悬浮物含量与光谱反射率的关系[J].城市环境与城市生态,2003,16(6):66 -68.
[22]黄嘉佑.气象统计分析与预报方法[M].北京:气象出版社,2004:36-47.
[23] Kirk J T.Estimation of the Scattering Coefficient of Natural Waters Using Underwater Irradiance Measurements[J].Australian Journal of Marine and Freshwater Reasearch,1981,32(4):533 -539.
[24] Whitlock C H,Pool L R,Usry J W,et al.Comparison of Reflectance with Backscatter and Absorption Parameters for Turbid Waters[J].Applied Optics,1981,20(3):517 -522.
[25] Gons H J.Optical Teledetection of Chlorophyll a in Turbid Inland Waters[J].Environmental Science and Technology,1999,33(7):1127-1132.
An Analysis of the Variation Features and Influential Factors of the Remote Sensing Reflectance of the Taihu Lake
QIAN Hao-zhong1,ZHAO Qiao-hua2,HE Jin-hai1,SUN De-yong2,JIANG Yu-wei2,TAO Rong-yin2
(1.College of Atmosphere Science,Nanjing University of Information Science and Technology,Nanjing 210044,China;2.College of Remote Sensing,Nanjing University of Information Science and Technology,Nanjing 210044,China)
The spectral data and numerical analyses of the Taihu Lake during the period of October 4-8,2010 were used to analyze the influence of solar zenith θ,the ratio of scattering and absorption coefficient b/a and parameter Q upon the variation of remote sensing reflectance.According to the results,remote sensing reflectance increases with solar zenith θ,while θ changes in the range of 0°~20°or 80°~89°,which has little influence on the growth of remote sensing reflectance.Remote sensing reflectance increases with the increase of b/a,and there obviously exists a positive relation between them.When Q is large(6~7),its alteration has little effect on the variation of remote sensing reflectance.On the contrary,when Q is small(2~3),its variation has enormous impact on the growth of remote sensing reflectance.Remote sensing reflectance tends to decrease with the growth of Q.
Remote sensing reflectance;Scattering coefficient;Absorption coefficient;Optical field distribution;Solar zenith
TP 751.1
A
1001-070X(2011)04-0100-08
2011-03-14;
2011-04-23
国家自然科学基金委“太湖混合层与真光层深度谱配置的时空变化规律、形成机制及其环境效应研究”(编号:41071070)和中国科技部“国家水体污染控制与治理科技重大专项”(编号:2008ZX07528-005)共同资助。
钱昊钟(1985-),男,硕士研究生,研究方向为气象及其环境效应。
赵巧华(1972 -),男,副教授,E -mail:qhzhao@nuist.edu.cn。
(责任编辑:刘心季)

