Davey-Stewartson方程组新的精确解*

刘绍庆,高存臣

(1.中国海洋大学信息科学与工程学院,山东青岛266100;2.山东科技大学公共课部,山东济南250031;3.中国海洋大学数学科学学院,山东青岛266100)

Davey-Stewartson方程组新的精确解*

刘绍庆1,2,高存臣3

(1.中国海洋大学信息科学与工程学院,山东青岛266100;2.山东科技大学公共课部,山东济南250031;3.中国海洋大学数学科学学院,山东青岛266100)

本文通过拓展的映射方法研究Davey-Stewartson方程组新的周期波解,并在极限情况下,得到了方程组新的孤波解以及其他形式解。

周期波解;Davey-Stewartson方程组;拓展的映射方法

0 引言

非线性微分方程的精确解的求法一直是数学物理工作者研究的热点。近年来,人们提出了许多强有力的求解方法,如Hirota双线性变换法[1]、反散射方法[2]、齐次平衡法[3]、Jacobi椭圆函数法[4]、F-展开法[5]等。新近提出的拓展的映射方法[6-8]被认为是Jacobi椭圆函数展开法全面的总结和概括。

本文考虑Davey-Stewartson方程组

其中u为复函数,v为实函数,r为实常数。该方程组最初是作为描述浅水波拟单色波包的模型由Davey和Stewartson[9]建立的。后来在考虑到表面张力影响时也导出了类似的方程组。在研究长短波相互作用中,若短波的群速与长波的相位匹配时也可导出方程(1),且此系统在等离子物理领域已有了应用。在文献[10-12]中,利用F-展开法和Weierstrass椭圆函数法导出了该系统的由Jacobi椭圆函数表示的周期波解,并且在极限情况下,得到了方程的孤波解和其他形式解。本文利用拓展的映射方法求出了Davey-Stewartson方程(1)新的周期波解,并且在极限的情况下,得到了方程(1)新的孤波解和其它类型的精确解,进一步揭示,Davey-Stewartson方程行波的运动性质,对流体力学的发展具有一定的参考价值。

1 拓展的映射方法

考虑如下形式的非线性发展方程

为求方程的行波解,令方程(2)具有如下形式解

其中k,λ是待定非零常数。

将(3)式代入方程(2)中,得到关于u(ξ)的微分方程

设u(ξ)具有下列形式

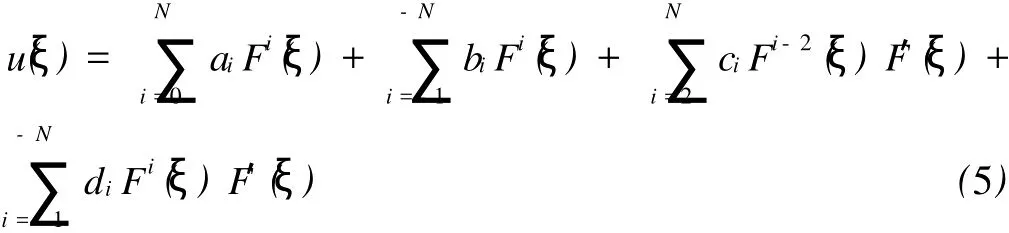
其中ai,bi,ci,di为待定常数,F(ξ),F′(ξ)满足

这里,P,Q,R为实常数,正整数N可由方程(4)中的u(ξ)最高阶导数项和非线性项之间的平衡来确定。

将(5)式代入方程(4)中,并利用辅助方程(6),将方程(4)化成F′i(ξ)Fj(ξ)的多项式,令F′i(ξ)Fj(ξ)的各次幂数的系数为0,得到关于ai,bi,ci,di,ξ的代数方程组。借助于Mathematica或Maple,求解上述代数方程组,并将这些结果代入(5)式便可得到方程(2)一般形式的行波解。

适当选取P,Q,R的值使辅助方程(6)的解F(ξ)是椭圆函数周期解,当椭圆函数的模m分别趋于1或0时,利用这些椭圆函数周期解,将得到方程的各种孤波解和其他类型的精确解。

2 Davey-Stewartson方程的周期波解

引进下列变换:

其中k,l,λ,α,β,γ为待定常数。

在λ=2α+2βl的条件下,将上述变换代入(1)得<(ξ),ψ(ξ)的微分方程:

将式(10)积分1次,并设积分常数为0,在此基础上再积分1次,得到

其中C为积分常数,将(11)式代入(9)式,得:

考虑(12)中<″和<3之间平衡得N=1,因此<(ξ)可以表示为:

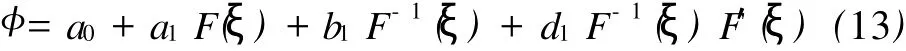
其中a0,a1,b1,d1待定且F(ξ)满足(6)。

将(13)代入(12)并利用(6)式,则(12)式就变成F′i(ξ)Fj(ξ)的多项式,令F′i(ξ)Fj(ξ)的各次幂项的系数为0,得到了关于待定常数的代数方程组:

解上述代数方程组得到下列2组解:

第一组:

第二组:

从而有如下形式的行波解

其中ξ=k[x+ly-(2α+2βl)t],η=αx+βy。由上述推导,有如下定理:

定理1 在非线性变换(7)～(8)下,系统(1)具有(14)～(15)的行波解或者(16)～(17)的行波解。

例如,如果利用表1,选择F(ξ)=ns(ξ),可以得到

当m→1时,可以得到新的孤波解:

表1 P,Q,R与方程F′2=PF4+QF2+R的解F(ξ)之间的关系表Table 1 Relations between values ofP,Q,Rand correspondingF(ξ)inF′2=PF4+QF2+R

当m→1时,可以得到新的孤波解:

当m→0时,可以得到新的孤波解:

注1:利用拓展映射方法可以得到新的周期波解,而(16)～(17)就是一类新型的解。

3 结论

拓展的映射方法是借助于1种新的Ansatz方程结合计算机的计算来建立非线性发展方程周期波解的方法。利用这种方法,本文求出了Davey-Stewartson方程新的周期波解,且在极限的情况下,得到了方程新的孤波解及其他形式解。

[1] Hirota R,Satsuma J.Soliton solutions of a coupled Korteweg-de Vries equation[J].Phys Lett A,1981,85(8-9):407-408.

[2] Wadati M,Konno K.Simple derivation of Bucklund transformation from Riccati form of inverse method[J].Prog Theor Phys,1975,53(6):1652-1656.

[3] Wang M L.Application of a homogeneous balance method to exact solutions of nonlinear equation in mathematical physics[J].Phys Lett A,1996,216(1-2):67-75.

[4] Fu Z T,Liu S K,Liu S D,et al.New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations[J].Phys Lett A,2001,290(1-2):72-76.

[5] Abdou M A.The extended F-expansion method and its applications for a class of nonlinear evolution equations[J].Chaos Soliton Fract,2007,31(1):95-104.

[6] Abdou M A,Zhang S.New periodic wave solutions via extended mapping method[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(1):2-11.

[7] Yomba E.Abundant families of Jacobi elliptic function-like solutions for a generalized variable coefficients KdV equation via the extended mapping method[J].Phys Lett A,2006,349(3-4):212-219.

[8] Abdou M A.New exact travelling wave solutions for the generalized nonlinear Schroedinger equation with a source[J].Chaos Soliton Fract,2008,38(4):949-955.

[9] Davey A,Stewartson K.On three-dimensional packets of surface waves[J].Proceedings of the Royal Socoety of London.Serries A,Mathematical and Physical Sciences,1974,338(1613):101-110.

[10] 张金良,任东锋,王明亮,等.Davey-Stewartson I的周期波解[J].数学物理学报,2005,25A(2):213-219.

[11] 许镇辉,李训牛,王树泽.Davey-Stewartson I型方程组的周期波解[J].聊城大学学报,2006,19(3):10-12.

[12] 刘常福,戴正德.Davey-Stewartson I型方程新的精确周期解[J].工程数学学报,2008,25(3):510-514.

New Exact Solutions of the Davey-Stewartson Equations

LIU Shao-Qing1,2,GAO Cun-Chen3
(1.College of Information Science and Engineering,Ocean University of China,Qingdao 266100,China;2.Department of Basic Courses,Shandong University of Science and Technology,Jinan 250031,China;3.School of Mathematical Sciences,Ocean University of China,Qingdao 266100,China)

This paper deals with periodic wave solutions for the Davey-Stewartson equations via the extended mapping method.In the limit cases,the solitary wave solutions and some type of traveling wave solutions for the system are obtained.

periodic wave solutions;Davey-Stewartson equations;the extended mapping method

O175.2

A

1672-5174(2011)03-111-04

山东科技大学科学研究‘春蕾计划’项目(2009AZZ051)资助

2009-07-06;

2010-04-13

刘绍庆(1977-),女,讲师。E-mail:carrielsq@gmail.com

AMS Subject Classification: 35Q20

责任编辑 朱宝象