基于自适应有限元法的基坑水平截面水头分布

胡 伟

(南华大学 数理学院,湖南 衡阳 421001)

基于自适应有限元法的基坑水平截面水头分布

胡 伟

(南华大学 数理学院,湖南 衡阳 421001)

利用自适应有限元方法理论并通过编程对基坑降水时水平截面的水头分布作了大量的数值模拟,得到了相应的结果,通过对结果的分析得到了与实际情况相符合的结果·

自适应有限元;数值模拟;渗流;水头分布

渗流是水工和岩土工程结构变形与稳定分析的一项重要的影响因素·非定常渗流研究是渗流的重要研究内容之一·随着计算机技术的发展,用数值模拟方法来研究渗流日益重要·有限元方法是渗流计算中最常用的一种数值方法·自适应方法已经在渗流计算中得到一定程度上的应用推广[1-3],主要应用的是自适应方法中的h-方法·h-方法在定常渗流计算中所取得的效果是明显的,但是对于非定常渗流,h-方法在应用上就有些困难了·对于非定常渗流,水力梯度随着时间变化,固定的网格剖分很难满足上述要求·本文应用自适应网格方法中的移动网格方法[4-5]计算非定常渗流.应用这种方法使得网格加密与稀疏化是随着水力梯度的变化自动实现的,这样就很好地解决了这个问题·

1 数学模型

含汇源项的二维的定常渗流与非定常渗流基本微分方程如下:

2 定解条件

(1)初始条件

如图1所示,工程要在一个矩形的江中小岛BCUV中央建设一栋高层建筑,为此需要在小岛中央开挖一个深达28 m的基坑GFMN·其中,BC=UV=210 m,BV=CU=240 m,GF=MN=50 m,GN=FM=80 m·

图1 基坑渗流水平截面示意图

基坑的边与小岛对应的边的距离都是80 m,初始水头为25.5 m,与江水持平,假设以v=1.6-0.05t(m/h)的速度对基坑实施降水,基坑降水过程中下着雨,每小时的降雨量为2 mm·于是,补水量Q=0.002 m3·已知渗流系数kx=ky=2.3 m/h,给水度μ=0.052,这里,Sx与μ在数值上是相等的·要研究的渗流区域是过基坑底面的水平截面的一半区域ABCDEFGW,另一半与它对称,其中,A W、ED为流量边界,q=0,其他边界为水头边界·

3 利用自适应网格法编程所得的部分结果

将上述数据对应地代入模型(2)及定解条件式(3)～(5)即可求解·其中的一些结果见图2～图9,这里时间t的单位为h·

图2 t=0时网格及水头分布(渗流场平面)

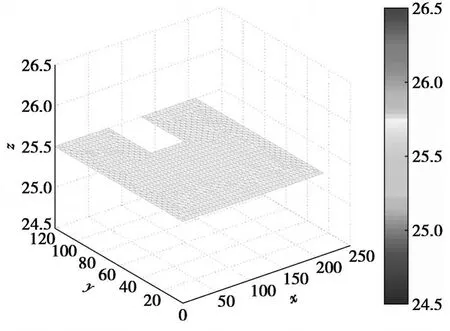
图3 t=0时网格及水头分布(解曲面)

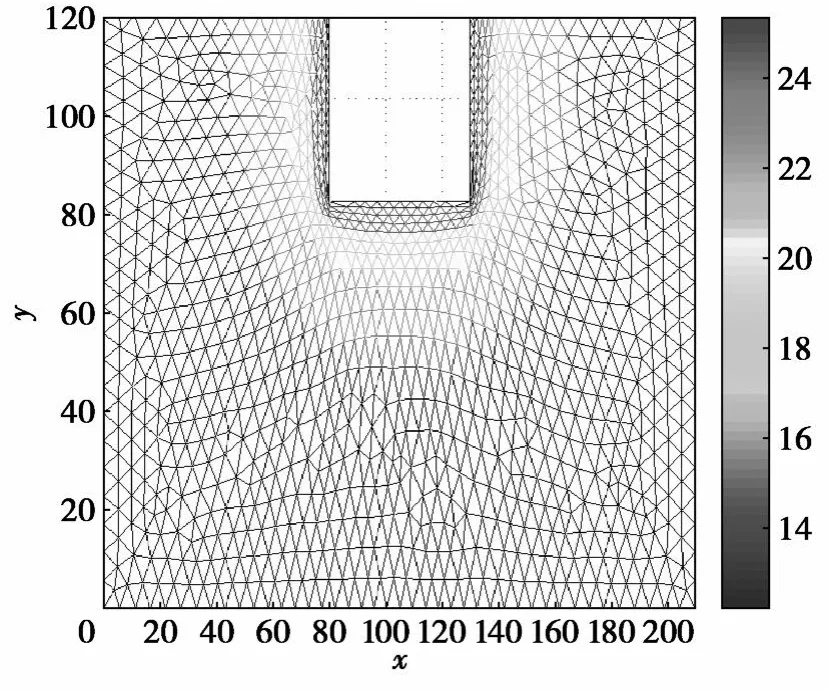
图4 t=10时网格及水头分布(渗流场平面)

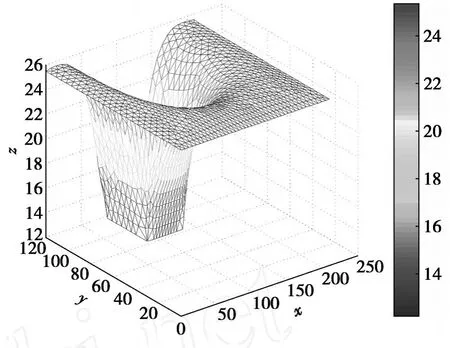
图5 t=10时网格及水头分布(解曲面)

图6 t=20时网格及水头分布(渗流场平面)

图7 t=20时网格及水头分布(解曲面)

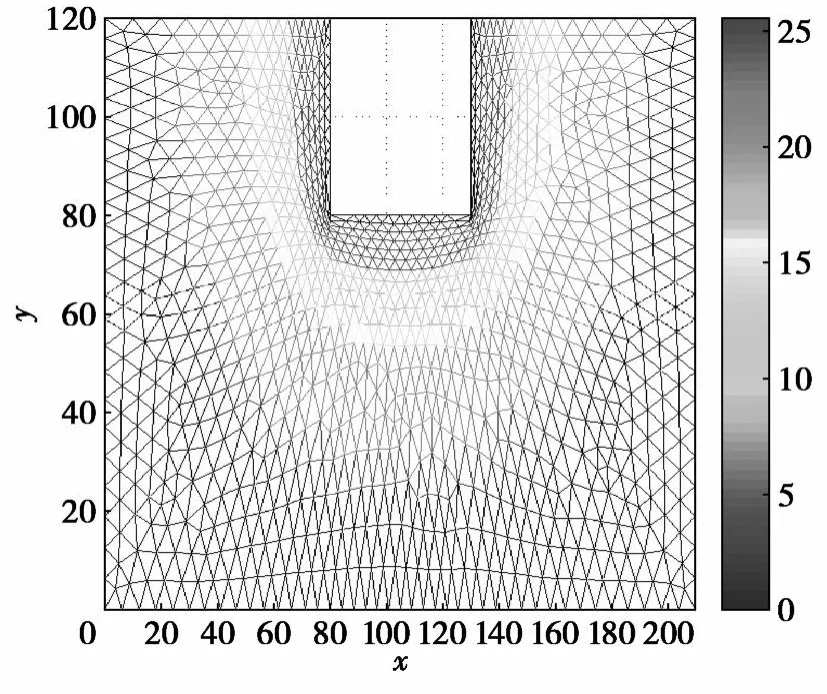
图8 t=30时网格及水头分布(渗流场平面)

图9 t=30时网格及水头分布(解曲面)

从图2、图4、图6、图8四个渗流场平面中可以看到,网格在水力梯度大的地方加密,在水力梯度小的地方稀疏·在这个例子中可以看到,由于渗流滞后于基坑内水位的下降,所以水头首先在基坑边界附近一个很小的区域内发生急剧变化·比较图2和图8,由于时间差别大,很容易看出以上变化,并且网格在这个区域加密,随着渗流的进行,这种现象向周围扩散·在这个基坑非定常渗流过程中,网格在基坑周围稠密,这样就可以更清楚地了解基坑附近的水头分布,这样的结果有利于准确评估基坑的安全性·同时,从图3、图5、图7、图9中,特别是在比较图3与图9时可以看出,网格在移动的过程中结点数不变,也就是说,在这个问题中,移动网格方法在保持计算量不变的情况下提高了整体解的精度,也给出了我们关注的渗流区域更详细的信息·

4 结 论

本文给出了一个数值求解偏微分方程的算例,从上述渗流计算结果可以看出,地基在基坑内水位降落过程中的动态渗流场有如下特征:一是受降雨的影响,在开始阶段,渗流场内部的水头略高于边界的水头;二是由于渗流滞后于基坑内水位的下降,所以水头首先在基坑边界附近一个很小的区域内发生急剧变化,网格在这个区域加密,随着渗流的进行,这种现象向周围扩散·在这个基坑非定常渗流过程中,网格在基坑周围稠密,这样就可以更清楚地了解基坑附近的水头分布·通过引进新的自适应方法,并实际应用在基坑实例中,很好地解决了以前一些方法的弊端,得到了不错的数值模拟结果,且结果图可视化·

[1] Rank E,Werner H.An adaptive finite element approach for the free surfaceseepage problem[J].Int.J.Num.Meth.Eng.,1986,23(7):1217-1228.

[2] Chung K Y,Kikuchi N.Adaptive methods to solve free boundary problems of flow through porous media[J].Int.J.for Num.And Ana1.Meth.in Geomech,1987,11(1):17-31.

[3] Burklcy V J,Bruch Jr J C.Adaptive error analysis in seepage problems[J].Int.J.Num.Meth.Eng.,1991,31(7):1333-1356.

[4] Li R,Tang T,Zhang P W.Moving mesh methods in multiple dimensionsbased on harmonic maps[J]. Journalof Computational Physics,2001,170:562-588.

[5] Li R,Tang T,Zhang P W.A Moving Mesh Finite Element Algorithm for Singular Problems in Two and Three Space Dimensions[J].Journal of Computational Physics,2002,177:365-393.

Water Head Distribution ofHorizontal Section of Foundation Pit Based on Adaptive Finite Element Method

HU Wei
(School of Mathematics and Physics,University of South China,Hengyang 421001,China)

Using the theory of adaptive finite element method,a lot of numerical simulations for the water head distribution of horizontal section in dewatering are made by programming.The results obtained are consistent with the actual situation.

adaptive finite element;numerical simulation;seepage;water head distribution

TV 223.4

A

1008-9225(2011)02-0014-03

2010-12-01

胡 伟(1986-),男,江西南昌人,南华大学硕士研究生·

【责任编辑:刘乃义】