中国象棋多自动机复合模型及其估值方法研究

张恩海,李彦平,朱俊威

(沈阳大学 辽宁省装备制造综合自动化重点实验室,辽宁 沈阳 110044)

中国象棋多自动机复合模型及其估值方法研究

张恩海,李彦平,朱俊威

(沈阳大学 辽宁省装备制造综合自动化重点实验室,辽宁 沈阳 110044)

应用离散事件动态系统有限自动机理论,建立了中国象棋多自动机复合模型·针对中国象棋机器博弈中传统静态估值方法对局面估值的不准确性,提出了动态估值方法·通过对原有的静态估值方法引入变量参数,提高了估值的准确性·

机器博弈;多自动机;静态估值;动态估值

机器博弈,又称计算机博弈,就是让计算机像人一样思维,进行棋类的博弈·1997年5月,计算机“深蓝”战胜了国际象棋大师卡斯帕罗夫,标志计算机在棋类博弈上已经超越了人类·事实上,“深蓝”的这种思维并不同于人类的智慧,虽然它战胜了国际象棋大师,但并不意味着计算机就比人脑聪明·

计算机缺乏的是人类的意识,在人机博弈中计算机获胜的原因在于其强大的计算能力·称其为“智能”还为时过早,只不过是从穷举出数万亿的可能情况中选择最好的棋步而已·然而,用人工智能来代替人脑或者协助人脑工作是我们不懈的追求·

近年来,作为人工智能学科的“果蝇”,计算机博弈日益成为人工智能工作者的主要研究对象之一[1]·

1 多自动机复合模型

在传统的系统与控制理论领域中,主要研究对象限于一类本质上属于物理世界范畴的连续变量动态系统,简称为CVDS·而离散事件动态系统是区别于 CVDS的另一类系统,简称DEDS[2]·DEDS由离散事件驱动,是本质离散的状态与事件按照一定的运行规则相互作用,进而导致系统状态不断演化的一类动态系统[3]·

中国象棋是广受欢迎的棋类游戏·通过对中国象棋的属性分析,不难发现,中国象棋博弈系统主要由两部分构成,即局面和招法·招法是驱动中国象棋博弈系统局面状态演变的基本因素·局面的状态都发生在离散时间点,即在招法给出时局面才能发生跃变,其他时刻保持不变,并且在空间中具有一种不连续的固有属性·招法的变化域和局面的状态空间也都具有离散性·基于以上因素,有理由认为中国象棋博弈系统属于离散事件动态系统,招法即是触发DEDS状态变化的事件[4]·

中国象棋博弈过程中,局面间的转换是由棋子的移动引起的,所以对其每个棋子建立模型是非常必要的·

在棋子a行走时,行棋规则和其他棋子会对棋子a的招法选择产生一些制约·表1为复合制约表,32个棋子组成一个二维表,该表能够清晰表现出每个棋子的可能招法,这样,32个有限自动机各自的行动和相互的制约都可以十分清楚地表达了出来·按照复合制约表和复合模型,32个棋子就可以自由行动起来·

在复合制约表中,KMM为棋子马/马的行棋规则,当KMM为真时,棋子马/马可行棋到目标位置 qij,即

表1 复合制约表

2 动态估值方法

估值方法和搜索算法,是中国象棋计算机博弈中的两大核心问题·估值方法的好坏直接影响棋力的高低·估值通常与博弈树搜索结合使用·由于在较少的步数内,一般难以将死对方·在难以判断输赢的情况下判断某一局面的好坏,可行的办法就是对局面进行量化,通过数值来衡量局面的优劣·估值需要考虑不同类型的象棋知识[5]·

在对局面估值时,预先设定好棋子的子力、位置、攻击、灵活度等类型知识的分值·当局面确定后,根据局面的信息直接调取对应类型的知识的分值进行加减运算,计算过程中不存在变量,这种估值方法称做静态估值方法·在中国象棋计算机博弈中,静态估值方法是普遍使用的估值方法·但该方法中预先设定好象棋类型知识的分值,是根据专家经验得出的,由于专业棋手的经验是随着对局的增加而增加的,因此提出动态估值方法,该方法在计算过程中,对静态估值方法中部分类型知识引入权值变量,权值变量随对局的增加而变化,能更有效地提高估值的准确性·动态估值方法下类型知识如下·

(1)子力·是棋子在某一局面下的价值·棋盘上的棋子的子力由棋子本身的价值、在棋盘上的位置和灵活度三部分组成·所以,某一局面的子力值为棋盘上所有己方棋子的子力之和,表达式为

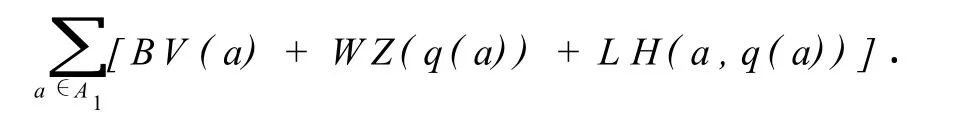
式中,BV(a)为棋子a的本身价值;W Z(q(a))为棋子a所在位置的分值;L H(a,q(a))为棋子a灵活度的分值·

(2)攻击·对弈的某一局面,从吃对方棋子的角度来表示对对方的威胁·如果己方棋子可以吃对方的某个棋子,就把对方棋子的子力据为己有·当己方棋子可以同时吃对方多个棋子时,因为一步只能吃一个棋子,所以将子力最大的对方棋子据为己有,其他的按一定比例占据·此比例系数可根据局面情况而定·最后把己方所有棋子的攻击分值求和,表达式为

(3)被攻击·同攻击值的定义相反,在某一局面下,己方棋子受到对方棋子的威胁,分值设定与攻击相似,但值为负数·显然,己方的攻击值等于对方的被攻击值的相反数,对方的攻击值等于己方的被攻击值的相反数·对方攻击值表达式为

(4)将帅安全·计算将帅是否受到威胁·设定一个安全区域,从己方将帅所在行算起,五行内如果有对方棋子,则说明己方将帅已经受到威胁,将帅安全的值也为负,其表达式为

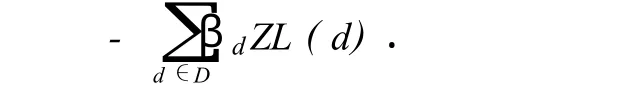
式中,ZL(d)为棋子d的子力;βd为比例系数,0＜βd,表示对方棋子对己方将帅的威胁程度;D是己方安全区域内的对方棋子的集合,d∈D·

(5)棋子配合·棋子配合是指棋子与棋子间的保护关系·重点是车/车、马/马、炮/的配合·当一个棋子被保护时,在棋子子力的基础上加上其他棋子的子力·因为该分值主要包含对局面起作用的配合,如将帅旁边的仕等,对局面的作用不是很大,所以要在子力前加一个比例系数,表达式为

己方对局面的估值是求取各项分值之和,不仅要计算本方的,还要计算对方的.本方为正值,对方为负值,其代数和即为当前局面的估值·己方局面评估值表达式为

显然,与静态估值相比,动态估值在原估值方法的基础上增加了参数αc,ηe,βd,γp,θj,ωk·参数确定方法如下(以红方为例):

第一步,取一象棋名局实例,要求该实例中带有红方转折性招法;

第二步,对该转折性走法后的局面进行估值,设值为

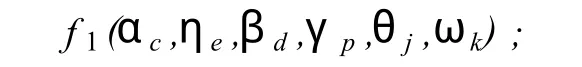
第三步,在博弈树下,与该局面同为一层的其他局面中取估值最大的局面,设其值为

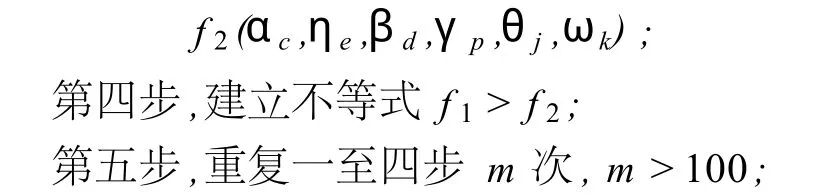
第六步,求解n元一次不等式组,求解参数的范围·

每测试一局,都会对参数的相互关系进行一次调整,随着测试局数的增加,参数的相互关系趋于稳定·通过对实战棋局的模拟,在参数相互关系下,手动调整如表2所示·

表2 手动调整表

验证此估值方法的优越性,采用中国象棋名局进行测试·如局面1至局面4所示,其为柳大华实战百局144局(湖北柳大华先胜杭州陈孝)中的四个局面,局面1、3是对方走棋结束,局面2、4是我方走棋结束(应手)·局面1到局面2是本局的转折,如图1形势,红方退车邀兑黑车,一击中的,使黑方阵势立即崩溃·从局面1到局面2有35种走法,对可能出现的35个局面分别估值,结果局面2分值最高,故我方选择局面2对应的走法·

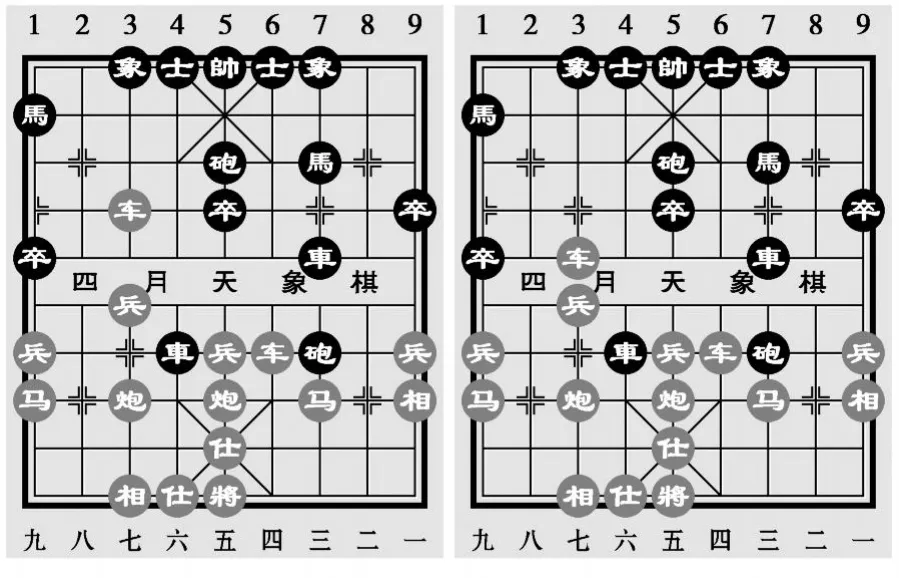
图1 局面1至局面2

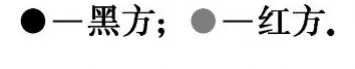
图2 局面3至局面4

局面3到局面4是红方稳定胜局的走法,如图2形势,红方退相调整阵势,红无后顾之忧·从局面3到局面4有46种走法,对可能出现的46个局面分别估值,结果局面4分值最高,故我方选择局面4对应的走法·

随着模拟棋局的增加,参数的值也趋于稳定·由象棋名局测试,可见该估值方法已接近象棋大师水平·

3 结 语

本文简单介绍了机器博弈·应用有限自动机理论对中国象棋建模·在传统静态估值基础上提出了引入权值的动态估值方法,并对估值的类型知识进行了重新设定,使局面的判定信息更加准确·通过对经典棋局的检验,该估值方法对局面的判定已接近象棋大师水平·

[1] 徐心和,邓志立,王骄.机器博弈研究面临的各种挑战[J].智能系统学报,2008,3(4):288-293.

[2] 郑大钟,赵千川.离散事件动态系统[M]·北京:清华大学出版社,2001.

[3] 徐心和,郑新颖.棋牌游戏与事件对策[J].控制与决策,2007,22(7):787-790.

[4] 徐心和,王骄.中国象棋计算机博弈关键技术分析[J].小型微型计算机系统,2006,27(6):961-969.

[5] 徐心和,王浩.孔凡禹事件对策理论及在棋类游戏中的应用[J].中南大学学报:自然科学版,2007,38(Sup1):718-721.

Multi-Automata Compound Model of Chinese Chess and Evaluation Methods

ZHAN G Enhai,L I Yanping,ZHU Junwei
(Key Laboratory of Manufacturing Industrial Integrated Automation,Shenyang University,Shenyang 110044,China)

According to the theory of discrete event dynamical systems(DEDS),a multi-automata compound model of Chinese Chess is established.The traditional static evaluation used in Chinese Chess game on computer currently could not reflect the information of situation accurately,so a method of dynamic evaluation is proposed.Moreover,by introducing parameter in the traditional method of static evaluation,the accuracy of evaluation is improved.

computer game;multi-automata;static evaluation;dynamic evaluation

TP 301.1

A

1008-9225(2011)02-0007-05

2010-11-10

张恩海(1983-),男,辽宁沈阳人,沈阳大学硕士研究生;李彦平(1957-),男,辽宁锦州人,沈阳大学教授,博士·

【责任编辑:刘乃义】