基于灰色系统理论的显著性项目造价估算方法研究
白海平, 景晨光
(1.北京铁路局,北京 100860;2. 石家庄铁道大学研究生学院,河北石家庄 050043)
目前,国内的工程造价计算方法主要是工程量清单法和定额概预算法,虽计算详细,但同时存在着计算工作量大、计算准确率较低、大量已完工程的工程数据也不能得到充分的利用等缺点[1]。此外,工程造价受多种因素影响,构成复杂,存在着造价信息具有较大的模糊性、可利用样本较小,贫信息等不完善问题,这种信息不完全确定的半封闭系统表现出一种高度的灰色状态,灰色系统理论在此方面具有独特的优势。与其他估算方法相比、由于灰色系统理论对样本没有严格要求,不需要样本服从任何分布,特别是它对时间序列短、统计数据少、信息不完全系统的建模与分析具有独特的功效,成为社会、经济、科教、技术等很多领域进行预测、决策、评估、规划、控制、系统分析与建模的重要方法之一[2-5]。以显著性项目为基础,通过建立时间序列,拟用GM(1,1)模型对项目实施过程已完工程的 CSIs进行预测,利用灰色系统理论的优势,以有效解决灰色状态下显著性项目造价估算在应用中的问题。
一、灰色系统理论模型
(一)灰色系统理论
灰色系统理论是有关灰色系统建立模型、控制模型、预测、决策、优化等问题的理论。该理论认为系统的行为现象尽管是朦胧的,数据是复杂的,但毕竟有序,是有整体功能的[6]。灰色预测方法是灰色系统理论的重要组成部分,是一种对含有不确定因素的系统进行预测的方法。通过鉴别系统因素之间发展趋势的相异程度,进行相关联分析,通过对原始数据进行生成处理来寻找系统的变化规律,生成较强规律的数据序列,建立相应的微分方程模型。
(二)数列GM(1,1)预测模型
灰色预测方法的特点表现在:首先是它把离散数据视为连续变量在其变化过程中所取的离散值,从而可利用微分方程式处理数据[7];对灰量、灰过程的处理是利用“生成”方法,求得随机性弱化,规律性强化的新数列,对非负数据,累加次数越多则随机性弱化越多,累加次数足够大后,可认为时间序列已由随机序列变为非随机序列。这样,可以抵消大部分随机误差,显示出规律性。灰色系统理论的微分方程称为Gm模型,G表示gray(灰色),m表示model(模型),Gm(1,1)表示一阶的、一个变量的微分方程模型。Gm(1,1)建模过程和机理如下:
记原始数据序列X(0)为非负序列
X(0)={x(0)(1),x(0)(2),x(0)(3),…,x(0)(n)}
其中,x(0)(k)≥0,k=1,2,…,n。
其相应的生成数据序列为X(1)
X(1)={x(1)(1),x(1)(2),x(1)(3),…,x(1)n)}
其中,Z(1)为X(1)的紧邻均值生成序列,均值生成常用于对历史数据不全的情况做出整理和补充。
Z(1)={z(1)(1),z(1)(2),…,z(1)(n)}
其中,Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1),k=1,2,…,n
称x(0)(k)+az(1)(k)=b为Gm(1,1)模型,其中a,b是需要通过建模求解的参数,若a=(a,b)T为参数列,且
则求微分方程x(0)(k)+az(1)(k)=b的最小二乘估计系数列,满足
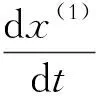
如上所述,则有
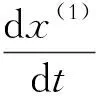
Gm(1,1)灰微分方程x(0)(k)+az(1)(k)=b的时间响应序列为
取x(1)(0)=x(0)(1),则
还原值
(三)灰色系统的检验

相对误差序列
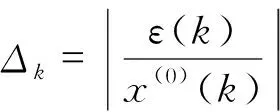
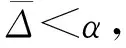
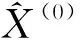
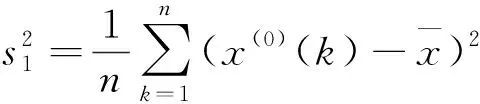
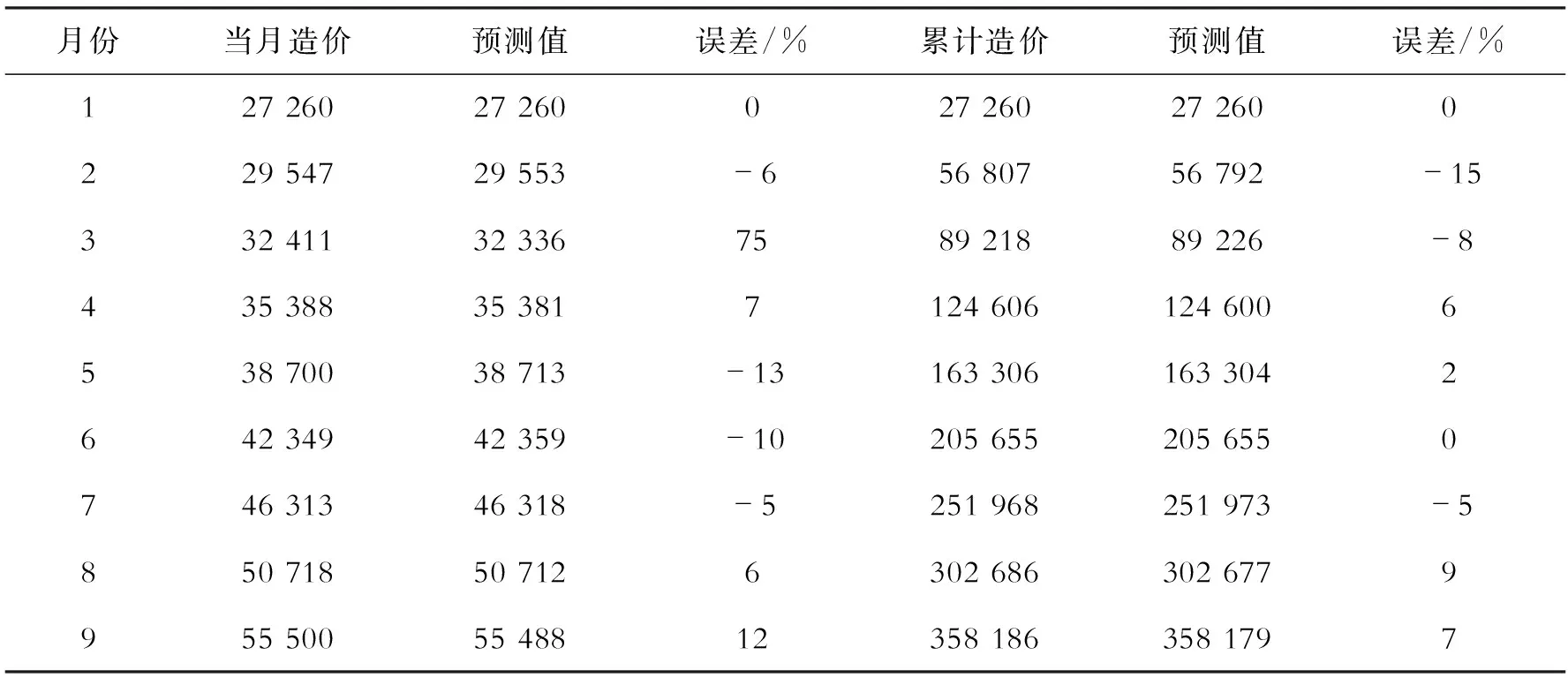
对于给定的c0>0,当c 19世纪末,意大利经济学家Vilfred Pareto 发现:社会的财富是不均匀分布的,大约20%的人拥有了社会80%的财富,这一发现被人们称之为“二八法则”,也称之为“显著性理论”, 即CS(Cost-significant,CS)理论。经过对大量已完工程的工程量清单进行研究,发现工程量清单中也有这样的规律:20%~30%项目的造价却占有工程总造价的70%~80%。国外在这方面已经有一些实证研究结果[8-10]。把工程量清单中分项工程的造价排在前20%的分项工程称为显著性成本项目(cost significant items,CSIs),其余的分项工程称为非显著性成本项目(non-CSIs)。按照“显著性理论”的思想,在考虑问题时就可以抓住对整个问题有重要作用的 20%着重解决和处理这20%,就可以既节省了时间和资源又解决了问题。尤其对于现在投资额上亿、上千亿的项目对显著性项目”造价的估算的把握有着重要的意义,如在现代的全生命周期显著性造价估算方法中,CSIs造价的测算尤为重要。如何区分工程项目的显著性成本项目CSIs和非显著性成本项目non-CSIs,一个简单易行的办法是用“均值理论”。均值理论表述如下:假设项目总成本为S,items个数是N,那么分部分项工程的平均成本就是S/N。把那些成本大于平均成本的分部分项工程,称之为显著性成本项目,小于平均成本的items,称为non-CSIs。如果CSIs不能保证在30%之内,可进行二次平均。 1.估算工程造价 大量的已完工程,不但其工程技术、施工方法等有可参考的价值,对于工程的造价也具有很大的参考价值。CSIs模型是建筑行业中造价估算中的一种简单的方法,它使得已完工程的造价数据得到充分利用,将工程投资估算花费时间和成本都降低了80%,并保证了投资估算的精确度。 2.控制工程投资 在工程的投资控制时,可以参照同类已完工程的CSIs,将投资控制的重点放在新建工程的CSIs上,这样做可以得到事半功倍的效果。 3.在投标报价中的应用 一个投标单位如果将曾经中标工程的历史资料都记录下来(包括工程概况、工程特征、中标价等等),建立一个数据库,那么当对新的工程进行投标时,可以参照历史资料,将新建的工程资料输入,就可以输出合理的投标报价。采用这样的方法,既充分的利用了以往的投标资料,又能更简洁、可靠地编制投标报价,从而更容易中标。 4.CSIs理论对大中型工程数据库建设的意义 在为这些包含有成千上万的分部分项工程的项目建立数据库的时候,既不能将所有的内容都存储起来,也不能概括性过强。CSIs理论为信息的取舍提供了一个非常有用的标准,具体建议就是数据库重点将工程的CSIs信息记录在内,而对于大多数non-CSIs分项只需作简略记录,有些甚至可以忽略。这样既节省了数据库建设的成本,又尽可能的保存了有用的信息。 显著性项目造价受多种因素影响,既有宏观因素,又有微观因素;既有确定性因素又有不确定性因素。造价的发生通常由许多因素共同所致。而这些因素间互相作用大小,对造价影响程度等都是不明确的,各因素的边界存在极大的模糊性和不确定性。构成显著性项目造价系统的各种关系是灰色的,如前所述,这个系统包括确定的、已知的信息,也包括不确定的未知的信息。基于这些考虑,完全可以把造价系统视为一个灰色系统,以显著性造价项目为研究对象,应用灰色理论进行研究分析。在项目实施过程中,每一阶段项目投资具有动态特征和不确定性,符合灰色系统的特点,可视为一个独立的灰色系统。 以某框架结构的多层住宅为研究对象,因为工程由于地质环境等诸多因素不同不具有类比性,在应用GM(1,1)模型时应区分不同情况进行区别对待,当前续CSIs和后续CSIs为同质时即为类似工程时,则可直接运用GM(1,1)模型预测下一阶段的ACWP,以下是第一种情况案例。 表1 某住宅小区显著性分项工程及其施工说明 表1中,“当月造价”是该月完成工程显著性项目的实际成本,“累计造价”是截至该月底已完工程显著性项目(CSIs)的实际成本即ACWP。表1中,“当月造价”中第1~4个月数据是GM(1,1)模型的输入数据,根据这4个数据计算模型参数;“当月造价”第5~9个数据作为检验数据。预测结果见表2。将施工过程中各个时点的ACWP看作一个灰系统,其各阶段增长具有内在联系,该法试图寻找ACWP各阶段数值的变化规律,在过去各时点数据已知的条件下,采用GM(1,1)预测下一阶段ACWP的值。具体预测过程如下:首先试建立Gm(1,1)模型的白化方程及时间响应式,并对Gm(1,1)模型进行检验,并预测该工程1~4月显著性项目造价。 X(0)={x(0)(1),x(0)(2),x(0)(3),x(0)(4)}=(27 260,29 547,62 411,35 388) X(1)={x(1)(1),x(1)(2),x(1)(3),x(1)(4)}=(27 260,56 807,89 218,124 606) 对X(1)作紧邻均值生成,令 Z(1)(k)=0.5x(1)(k)+0.5x(1)(k-1) Z(1)={z(1)(1),z(1)(2),z(1)(3),z(1)(4)}=(27 260,42 033.5,73 012.5,106 912) 于是, 设 由于 a=-0.089 995,b=25 790.28 可得Gm(1,1)模型的白化方程: 其时间响应式为: (27 260,29 553,32 336,35 381) 残差序列为 ε(0)=(ε(0)(1),ε(0)(2),ε(0)(3),ε(0)(4))=(0,-6,75,7) Δ= (0,0.000 2,0.002 31,0.000 2)(Δ1,Δ2,Δ3,Δ4) 平均相对误差: 模拟误差Δ4=0.000 2=0.02%<0.01,精度一级。 |S|= 计算均方差比: 计算小误差概率: 0.674 5S1=2 058.40 所以, 小误差概率为一级,故可用: 进行预测,5~9月显著性项目造价预测值为: 表2 某住宅小区2005年1~9月份实际造价ACWP 万元 根据预测结果,基于灰色系统方法对显著性项目造价的估算与实际显著性项目造价结果及其相近,精度较高,检验误差均为一级,ACWP造价预测误差不超过10%,证明用基于时间序列的灰色GM(1,1)模型预测显著性项目造价是可行的。 灰色预测具有所需数据少,对邻近时期的预测精度较高,而对长期预测精度差,只能进行趋势预测的特点。根据预测结果采取预控措施,也体现了事前进行投资控制的一种方法。对某住宅小区的案例实证表明,该方法对于预测临近时期的ACWP具有较高精确度。灰色模型建模相对那些复杂建模有简练、易得等特点,并且通过一次累加基本克服了数据的随机性,使规律性更加明显。灰色理论利用处理已知数据的方法来寻找过去统计数据间的规律,弥补了数理统计方法因数据过多带来计算量过大的缺陷,并且扩大了其应用范围。但该模型仍存在不足之处,如将造价的连续数据直接离散化过程,会造成造价误差的加大,与实际值相差甚远;直接采用数据均值生成序列也过于随意,在以后的造价估算研究中该模型仍有进一步改进的空间。 参考文献: [1]段晓晨.工程造价计算原理[M].北京:中国铁道出版社,2000. [2]羊英姿,麦继婷.利用灰色关联理论估测市政管道造价[J].四川建筑,2006(5):158-159. [3]关宇.一种基于灰色系统的建筑工程快速估价方法[J].当代建设,2003 (2):30-31. [4]肖燕彩,陈秀海,朱衡君.改进的离散灰色模型及其应用[J].北京交通大学学报,2008(3):2-15. [5]张传友.灰色系统理论在建筑工程快速估价中的应用[J].福建工程学院学报,2006(1):64-67. [6]段晓晨.政府投资项目全面投资控制理论和方法研究[M].北京:科学出版社,2007. [7]邓聚龙.灰色系统理论教材[M].武汉:华中理工大学出版社,1990. [8]Dojerty, Paul. Total Cost management in the Internet Age [C].AACE-I TRANSACTIONS 1998. [9]Batten, Roger M. Energy and Cost-Total Cost Management Discussion: the Global Gas Industry[J]. COST ENGINEERING, SEPTEMBER 1995,37(9):39-49. [10]Campi,JohnP.Total Cost Management at Parker Hannifin [J].MANAGEMENT ACCOUNTING January 1989:37-46.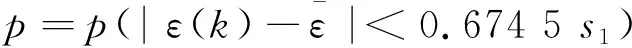
三、CSIs理论
(一)显著性理论
(二)CSIs模型的实际应用
(三)显著性项目造价与灰色系统的关系
四、灰色GM(1,1)模型在显著性项目造价估算中的应用
(一)模型的建立

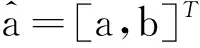
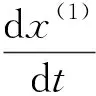
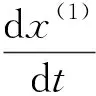
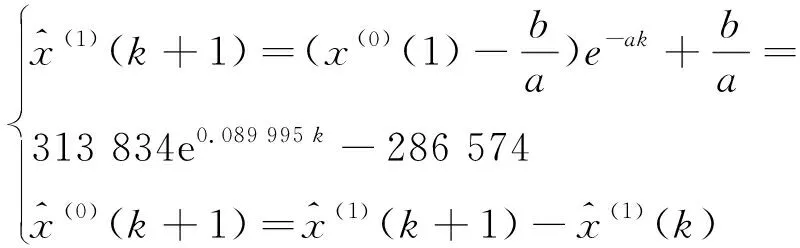
(二)精度检验
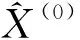
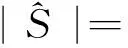
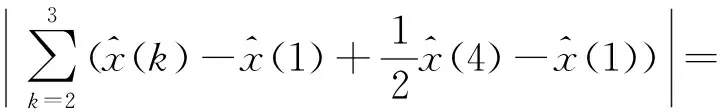

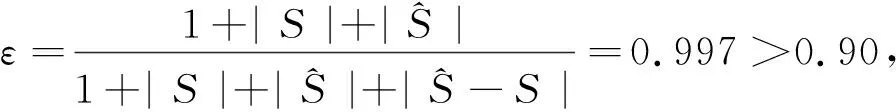
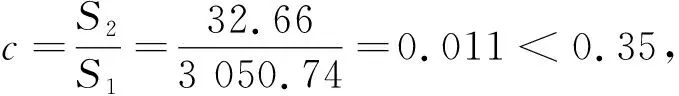
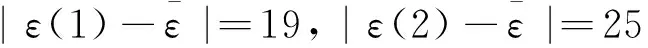
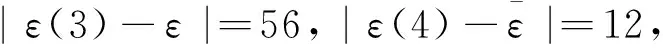
五、结论与评价

