模糊数学在员工绩效评价中的应用研究

杨丽雯

(哈尔滨商业大学管理学院，黑龙江哈尔滨 150028)

［人力资源］

模糊数学在员工绩效评价中的应用研究

杨丽雯

(哈尔滨商业大学管理学院，黑龙江哈尔滨 150028)

员工绩效评价的实际操作中有很多难以界定的模糊性因素，包括指标内涵、评价标准以及评价过程中的主观性等。而对于这些外延模糊、内涵无法精确界定的模糊因素，其评价和管理都存在相当大的难度。采用科学的绩效评价标准和评价方法进行员工绩效评价成为企业绩效管理关注的焦点。运用模糊数学中的几种方法对员工绩效评价中存在的模糊问题进行精确化处理，从而增强了绩效管理的有效性和准确性。

员工绩效评价;模糊数学;隶属函数

绩效评价在西方被很多专家学者认为是人力资源管理中最难处理的问题。因为在实际的绩效管理中很多难以量化指标的界定内涵以及标准具有很大的模糊性，主要依靠主观评价，从而使绩效评价结果缺乏客观性，使绩效管理很难顺利进行。模糊数学是一门新兴学科，已初步应用于模糊控制、模糊识别、模糊聚类分析、模糊决策、模糊评判、系统理论，在信息检索、医学、生物学、气象等方面已有具体的研究成果。模糊数学应用到员工绩效评价中，可以增强绩效管理的准确性和有效性，在模糊中寻求精确，在精确中包含模糊，推进评价者和评价对象之间关系的定量和定性分析相结合的过程。

一、员工绩效评价模型的构建

1.三角模糊数

三角模糊数TRFN是一种典型的模糊数。若实数域上的模糊集~A可用一个三元数组描述的三角分布函数表示，且有隶属函数:

2.梯形模糊数

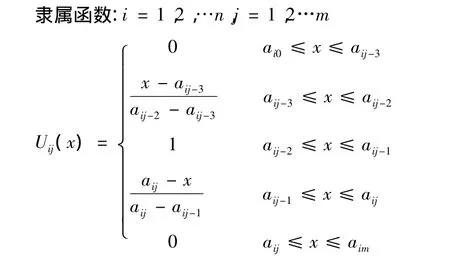
在员工绩效评价中，可利用梯形模糊数定义定量指标评价集，假设绩效评价总值为100，确立评价集;并且可根据具体标准值以及员工实际值计算员工在某项指标的分值。

3.重心法逆模糊化

基于以上的隶属函数的建立，为了使梯形模糊数与三角模糊数转化为精确值，即要通过一定的算子进行逆模糊化处理。本文采用一种较常用的方法——重心法，对评语等级集进行处理。

~A=(a，b，c，d)，若u(x)为隶属函数，当b≠c时为梯形模糊数，b=c时为三角模糊数。公式如下:

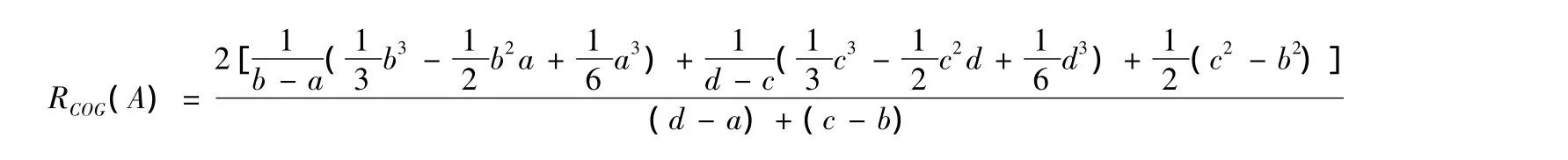
按照此方法进行去模糊化处理得出结果。

(1)关键事件法

关键事件法是由美国学者福莱·诺格(Flanagan)和伯恩斯(Bens)在1954年共同创立的，指那些会对公司、部门或个人的整体工作绩效产生积极或消极的影响的重大事件(行为及其结果)。管理者将一个员工的绩效判断为“优秀”、“良好”或者“一般”、“差”、“很差”需要一些证据做支持。由上级主管记录员工平时工作中的关键事件，在预定的时间内(通常是半年或一年之后)利用积累起来的记录，对被考评者的绩效做出判断和评价的方法。

(2)多准则模糊决策矩阵

4.模糊综合评价法

模糊综合评价法实质上是一种定量评价法，评价者从影响问题的主要因素出发，参照有关数据和情况，通过模糊数学提供的方法进行运算，得出定量的综合评价结果。在模糊综合评价时，所需要的主要数据是各个指标的权重因数和指标的评定等级。一般来说，运用模糊综合评价法对销售人员进行考核时，首先确定给出评价指标的因素集:评价指标集R={R1，R2，R3，R4，R5}，并且确定各个评价指标的权重，W=(ω1，ω2，……ωn)，并且∑ωi=1;给出评语等级集E={e1，e2，e3，e4，e5}，利用(1)Ai= Wi*Ri，(2)Fi=Ei*Ai，(3)B=WF三个步骤求出总分值。

二、实证分析

现以A大型家电企业哈尔滨分公司销售部B销售人员为研究对象进行实证分析。

在收集资料的过程中，定量指标通过访谈法(与公司人力资源部门以及财务部门进行沟通，与公司销售部门领导进行接触)，定性指标通过调查问卷法(对评价客体的同事、上司发放调查问卷)进行数据与信息的获取。

首先，确定A集团哈尔滨分公司销售人员绩效定量指标评分标准。对所取得资料中的数据进行整理，对于评语集进行定义，在“很差”、“差”、“中”、“好”、“很好”中，“中”的标准为基本达到公司或者部门所要求的目标。“很差”代表远远低于行业均值或者该企业均值，有突发情况或者该员工很难有改进空间，如表1所示:

表1

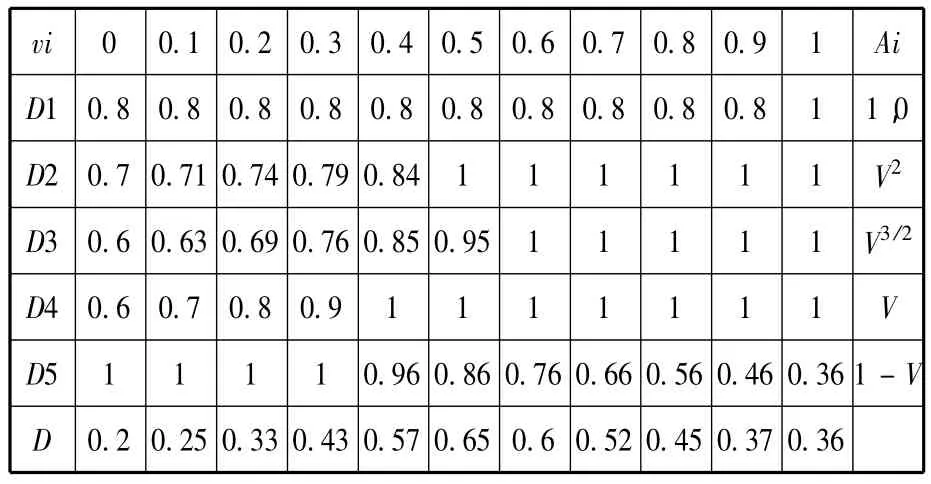
现取得A集团哈尔滨公司销售人员定量指标标准值以及B人员数据。根据了解所得，B人员进入公司2年，业绩成绩属于中上水平，在公司表现良好。经过统计分析得出选择其作为样本更具有代表性。根据梯形模糊数隶属函数确定各定量指标的模糊数，如表2所示。

通过表2计算得出定量指标R1的隶属度如下:

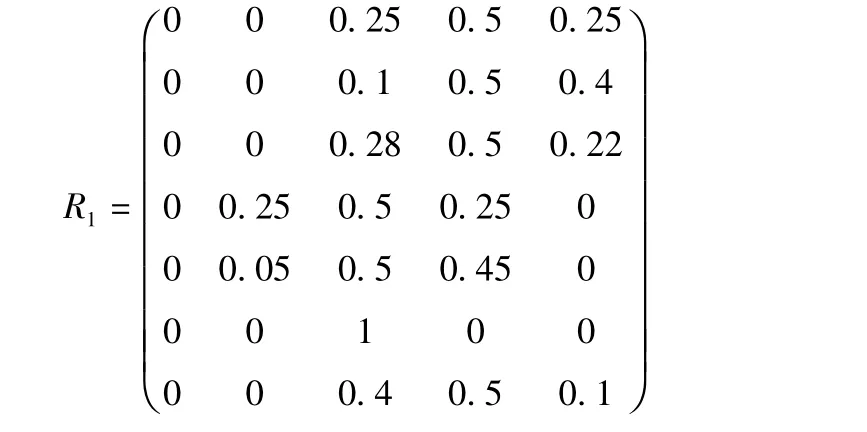
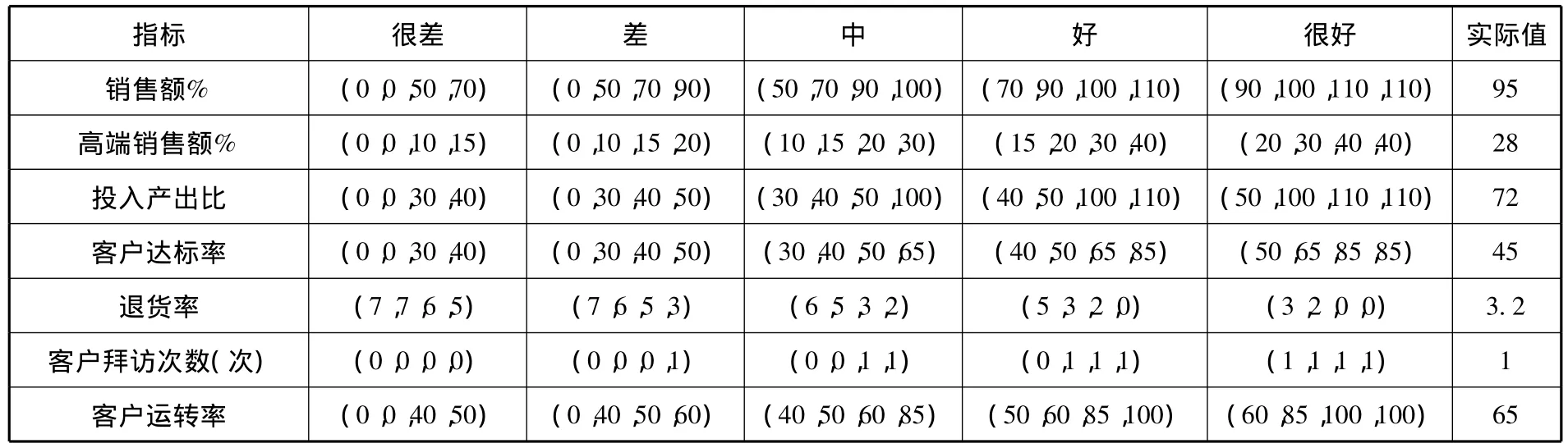
表2

其次，对定性指标的评价主要根据评价指标关键事件法来设置调查问卷，分发给评价对象的同事与上司。一共分发10份问卷，回收问卷10份。对10份问卷进行统计分析。根据关键事件法得出的结果评定所评价指标的归属等级，采取多准则决策矩阵计算其所属等级隶属度。下面以“有效沟通”为例。

设立五个关键事件来作为评价标准:U=(U1，U2，U3，U4，U5)。

U1为与人配合达成工作要求;U2为表达自己的意见想法;U3为擅于协调主持工作;U4为处理复杂人际关系; U5为影响他人并获得他人支持。

若能与人配合达到工作要求，擅于表达自己，熟练协调主持工作，能够处理复杂的人际关系，获得周围人的支持，非常好地进行了有效沟通，则A1=min(U1，U2，HU3，U4，U5)

若能与人配合达到工作要求，擅于表达自己，熟练协调主持工作，能够处理人际关系，很好地进行了有效沟通，A2=min(U1，U2，HU3，U4)。

若能与人配合达到工作要求，擅于表达自己，熟练协调主持工作。较好地进行了有效沟通则，A3=min(U1，U2，U3)。

若能与人配合达到工作要求，擅于表达自己，达到有效沟通的目的，则A4=min(U1，U2)。

若既不与人配合完成工作，不擅于表达，不会处理复杂的人际关系，没有协调主持工作的能力，无法实现有效沟通，则

通过收集资料获知，该名员工积极配合同事完成工作，协调主持工作能力很强，表达能力与处理复杂人际关系能力一般。初步进行评价并根据归属等级计算，由此判定U=(U1，U2，U3，U4，U5)=(0.7，0.4，0.8，0.3，0.2)计算得出，C(u)=(0.2，0.3，0.4，0.4，0.64)

vi 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 Ai D1 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 1 1，0 D2 0.7 0.71 0.74 0.79 0.84 1 1 1 1 1 1 V2 D3 0.6 0.63 0.69 0.76 0.85 0.95 1 1 1 1 1 V3/2 D4 0.6 0.7 0.8 0.9 1 1 1 1 1 1 1 V D5 1 1 1 1 0.96 0.86 0.76 0.66 0.56 0.46 0.36 1－V D 0.2 0.25 0.33 0.43 0.57 0.65 0.6 0.52 0.45 0.37 0.36

结果为，这位销售人员有效沟通在A2这个等级的隶属度为0.52。

同样可以求出其他指标所属等级的隶属度，简化过程，得出R2为能力素质方面的隶属度矩阵。

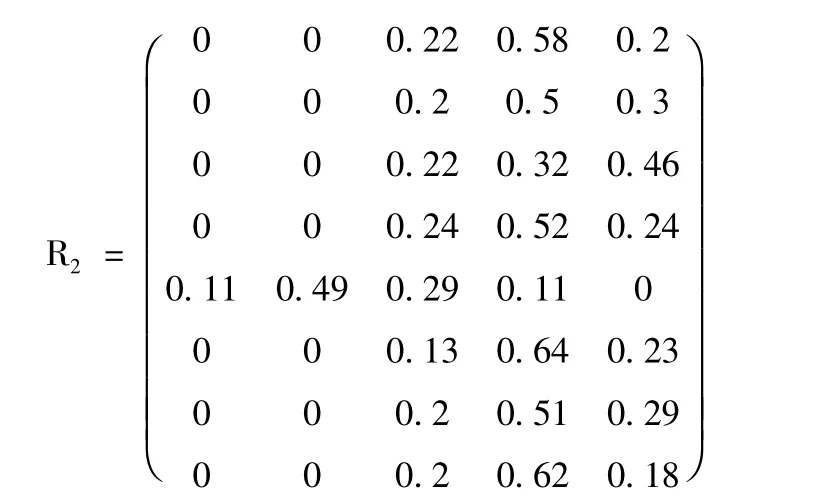
最后计算出子因素层对于准则层的权重Wi，根据模糊综合评价A=W*R得出准则层隶属度以及总隶属度，并且根据模糊数评价集分值计算出员工绩效评价分数。

根据以上计算得出:很差隶属度为0.004，差隶属度为0.025，一般隶属度为0.309，良隶属度为0.442，优隶属度为0.22。从而该员工表现良好，总分数为66.95分。能力素质较好，发展空间较大。

三、结论

把模糊数学应用到员工绩效评价当中去精确绩效管理过程中的一些模糊因素，运用多种模糊数学方法从定量指标与定性指标两方面来进行精确计算。在定量指标中，把评价标准模糊化，通过隶属函数确定隶属度。对于定性指标来说，主要根据指标的关键事件法中每个因素进行评价，借由多准则决策模糊矩阵求出评价客体所属等级的隶属度，从而使定性指标的评价更加精确。最后运用模糊综合评判与三角模糊数和梯形模糊数确定的精确分值求出员工的最终分值。

［1］张俊霞．基于模糊综合评价方法的企业员工绩效评估［J］．东北农业大学学报，2009(4):93－95．

［2］蔡志强．模糊数学在人力资源管理绩效评价中的应用［J］．数学实践与认识，2006(1):212－216．

［3］胡宝清．模糊理论基础［M］．武汉大学出版社，2004．

［4］冯宝成．模糊数学实用集粹［M］．中国建筑工业出版社，1991．

F061.1

B

1002－2880(2010)11－0142－03

(责任编辑:梁宏伟)