实验数据处理的excel函数解法研究

熊泽本

(荆楚理工学院,湖北荆门 448000)

实验数据处理的excel函数解法研究

熊泽本

(荆楚理工学院,湖北荆门 448000)

回归分析是一类数学模型,其研究对象是一个随机变量同一个或多个非随机变量的关系问题,在提出一元和多元线性回归的基础上,通过比较最小二乘法解法和 Excel函数解法,指出 Excel函数解法可以简化复杂的数学运算,并配以图表,给求解过程带来方便。

回归分析;最小二乘原理;Excel函数解法

在物理、化学实验中,很多实验数据的处理都要求研究自变量和因变量之间的关系,确定由该两个变量所决定的曲线和最佳拟合参数。由一个或一组随机变量来估计或预测另一个随机变量的期望值时建立的模型及所作的统计分析,这类问题的研究称作回归分析[1]。当只有一个自变量和一个因变量,且它们是线性关系时,称为一元线性回归:当自变量个数大于1,且因变量与自变量仍为线性关系时,称为多元线性回归。

1 线性回归模型及矩阵解法

设因变量y和自变量x1,x2,…,xk满足以下线性关系:

y和x1,x2,…,xk作 n次试验,所得数据为(yi,xi1,xi2,…,xik)(i=1,2,…n)他们满足以下线性关系:

写成矩阵形式即:

其中

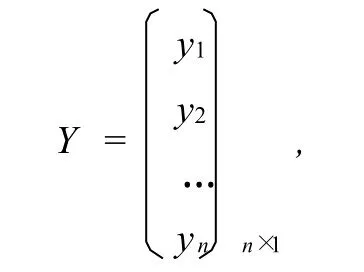
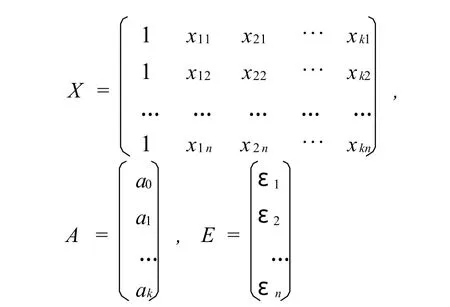
上式中,a0,a1,…,ak是回归系数,ε1,ε2,…,εn是n个相互独立且服从同一正态分布n(0,σ)的随机变量。

为了总结回归分析的计算结果,也为了检验回归分析的可信程度,通常的做法是列出它的回归分析表,如表1所示。

表1 方差分析表

2 Excel函数解法

上述回归分析过程若用人工计算则过程繁琐且计算量巨大,若借用计算机和相关软件可使求解过程大为简化。Excel是office系列办公软件的一个组件,它提供了大量的函数,运用这些函数可以进行统计管理、线性分析等工作,并且可以利用它强大而丰富的的图表功能清晰显示变量之间的关系。(1)式中若自变量只有一个,即为一元线性回归模型,对于一元线性回归问题可用文献[3]中的 Excel统计函数 FORECAST、SLOPE、INTERCEPT,这三个函数就能够简单地完成[3]。但是文献[3]解法仍显繁琐,必须调用 SLOPE、INTERCEPT两个函数才能分别求出表示为Y=a+bx的回归直线的斜率b和截距a,而且上述两函数只能求解一元回归而不适用于多元回归。实际上对一元或多元回归问题均可用Excel的统计函数LINEST求解。

2.1 回归分析的函数解法

LINEST函数是使用最小二乘法对已知数据进行最佳直线拟合,并返回描述此直线的数组。因为此函数返回数值数组,所以必须以数组公式的形式输入。

设回归方程为:或 y=a0+a1x1+a2x2+…+akxk(多元回归)式中若 y、x和a是向量。则LINEST函数返回的数组为{ak,ak-1,…,a1,a0}。LINEST函数还可返回附加回归统计值。

函数的语法

数组known-x’s可以包含一组或多组变量。如果只用到一个变量,只要known-y’s和knownx’s维数相同,它们可以是任何形状的区域。如果用到多个变量,则 known-y’s必须为向量(即必须为一行或一列)。

Const 为一逻辑值,用于指定是否将常量a0强制设为0。

如果const为 TRUE或省略,a0将按正常计算。

如果const为 FALSE,a0将被设为0。

Stats 为一逻辑值,指定是否返回附加回归统计值。

如果stats为 TRUE,则LINEST函数返回附加回归统计值,这时返回的数组列表如表二所示;如果 stats为 FALSE或省略,LINEST函数只返回斜率a和截距a0。

表2 LINEST函数返回附加回归统计值

2.2 应用实例

为了测试某种钢板的屈服强度σs(MPa)与厚度x1(mm)、含碳量百分比x2、含铬量百分比x3的关系,对20块钢板进行测试,测试数据如表3所示:求σs对x1、x2、x3的多元回归函数。

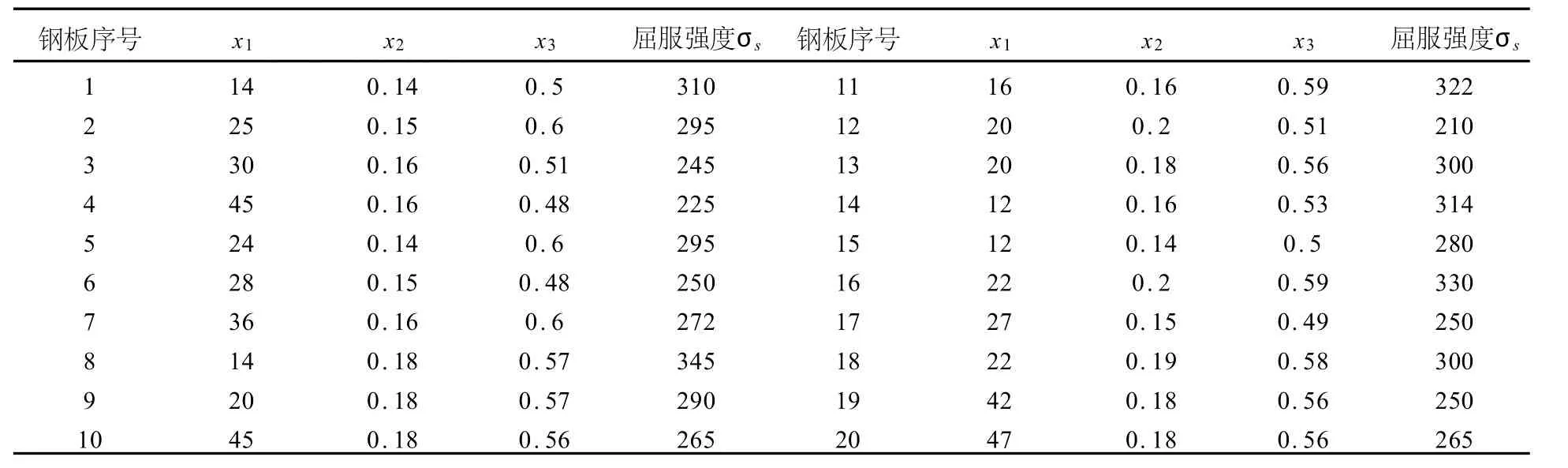
表3 试验数据表

2.2.1 求解步骤

(1)启动 Excel,录入表三所示数据。(2)在Excel中选择单元格 H1,选择“插入”菜单中的“插入函数”选项,在弹出的“插入函数”对话框中选择“常用函数”类型中的“LINEST”函数。如图1所示:单击“确定”按钮,会弹出“函数参数”对话框,如图2所示。(3)在“函数参数”对话框中 Y值输入区域“Known_y’s”中输入因变量 Y的样本数据区域,在X值输入区域“Known-x’s”中输入因变量X的样本数据区域。Const和Stats两个逻辑值均设为 TRUE。(4)注意公式必须以数组公式的形式输入。在将公式输入到单元格 H1后,选择以公式单元格开始的区域 H1∶K5。按F2,再按Ctrl+Shift+Enter。如果公式不是以数组公式输入,则返回单个结果值467.0440533。当作为数组输入时,将返回以下回归统计值的分析结果,见表4。

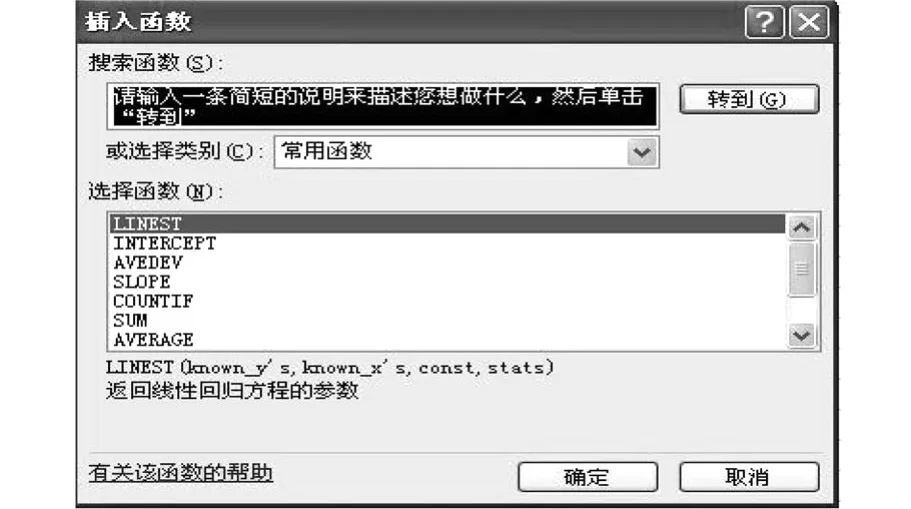
图1 “插入函数”对话框

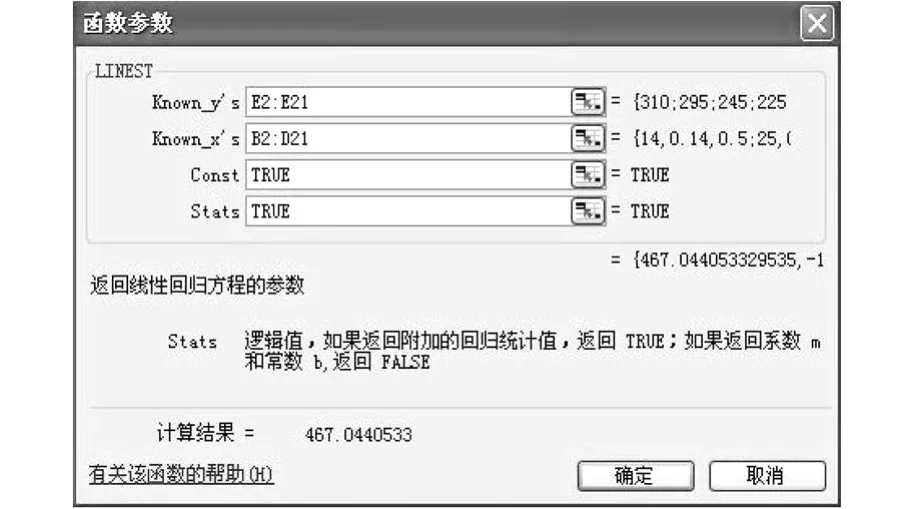
图2 “插入函数”对话框

表4 LINEST函数返回附加回归统计值表

2.2.2 回归结果分析

由表四输出结果可得如下结论:⑴多元线性回归方程的参数a3、a2、a1、a0分别为:490.5930346、-168.96223、1.792472、87.2062故所得回归方程为:

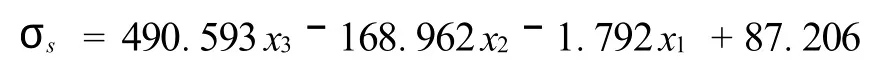
(2)回归方程的判定系数R2的值为0.666618,F统计值为10.66435,因LINEST函数系统默认显著水平为α=0.05,经查表F0.95(3,16)=3.24,很显然有F＞F0.95,则可认为该方程的可信度是95%。(3)由于第一自变量的回归系数绝对值远小于第二、第三自变量的回归系数的绝对值,由此可知:第一变量对Y值影响不大,而第二、第三变量对Y值影响非常显著,即:钢板的屈服强度主要取决于其含碳量和含铬量,而与其厚度关系不大[4]。所得分析结果符合试验客观实际。

3 结 论

从以上分析过程可以看出:利用 Excel的LINEST函数的回归分析功能可以简化大量的数据运算和误差分析过程,又可以利用 Excel强大的图表功能描绘物理曲线。同时有利于培养学生的计算机运用能力,提高实验速度,应该在实验中推广。

[1]中山大学数学系.概率论与数理统计[M].2版.北京:高等教育出版社,1988.187-188,237-238.

[2]王文健,许荔,钱海挺,等.试验数据分析处理与软件应用[M].北京:电子工业出版社,2008:64-69.

[3]郭志军.Excel在线性回归分析中的应用研究[J].张家口职业技术学院学报,2009,24(3):52-56.

[4]刘天琦,支敏学,朱杰远,等.双真空熔炼(VIM+VAR)30CrMnSiNi2A钢屈服强度的影响因素分析[J].材料工程,2003(5):11-14.

The Applied Research of Excel Functions in Experimental Data Processing

XIONG Ze-ben

(Jingchu College of Science and Technology,Hubei,Jingmen 448000)

Regression analysis is a process of constructing mathematical model which focuses on the relation between stochastic variable and non-stochastic variable.Based on the analysis of linearity return problem,this article works out the solution tOit-least squares method and the Excel solution law.With the comparison of these twOmethods,it can be found that Excel,with the aid of graphs,can clearly display data relations when solving return problems,sOthat office eficiency will be achieved greatly.

linearity regression analysis;least squares method;Excel function

04-39

A

1007-2934(2010)06-0086-04

2010-09-14