驻波法测定声速实验的matlab模拟
张春梅
(北京印刷学院,北京 102600)
驻波法测定声速实验的matlab模拟
张春梅
(北京印刷学院,北京 102600)
在驻波法测定声速实验中,根据发射器和接收器之间合成声场的位移波动方程和声压波动方程,用matlab程序模拟了声场和声压的振幅和初相位分布,并对模拟结果进行了分析和讨论。
驻波法;matlab;模拟
驻波法测定声速是理工科院校普遍开设的一项物理实验,实验装置图如图1所示。信号发生器输出的电信号加在激发换能器S1上,由于逆压电效应,S1成为超声波源,发出一束超声波在空气中传播,当超声波到达接收换能器S2后,一部分被反射回去,这样两列波在S1和S2之间可以形成干涉。换能器S2接收面上的共振信号由压电效应转换为电信号输入示波器,移动S2的位置,在移动的过程中,示波器中显示的信号大小呈周期性变化,当出现极大值时,即为形成驻波的位置,两个相邻极大值所对应的S2位移为λ/2,根据波长和信号发生器的频率,即可得出超声波在空气中的传播速度[1-2]。
当前的实验教材在介绍原理时,普遍是将激发换能器和接收换能器之间的叠加波视为驻波进行讨论。但在实际的实验中,两个换能器之间的声波叠加,并不是真正的驻波,而是显示出驻波加行波的特征;在示波器中观察到的波形,也并非是驻波产生的位移波形,而是驻波加行波产生的声压所转化的电信号[3-5]。本文对这些问题进行了讨论,并对叠加波和声压的振幅和初相位分布进行了matlab模拟,直观的给出了驻波加行波的传播规律以及声压的变化规律,并讨论了模拟结果。通过实验模拟,使抽象的问题变得直观化,加深了学生对物理本质的理解,对实验教学起到了一定的促进作用。
1 驻波法的讨论及matlab模拟
如图1所示,S1为激发换能器,将它产生的超声波记为正向波,正向波到达接收换能器S2后,被接收的同时,还要反射一部分超声波,成为反向波,两列方向相反的行波在S1和S2之间进行叠加,形成干涉。设S1和S2之间的距离为L,S1处为
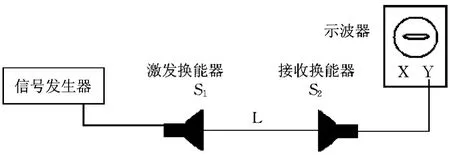
图1 声速测定实验装置图
原点O,Ox轴沿着S1S2向右,则S1产生的声波动方程为:
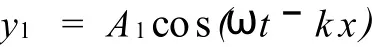
在S2上反射后,由于声波在界面上反射时出现半波损失,反射后的波动方程为:

只有当L=nλ/2时,y2=A2cos[ωt+kxπ)],两列波在S1和S2之间相遇,才能形成驻波。则根据波的叠加原理,当L=n*λ/2时,合成的声场波动方程为[6]:

=2A2sinkx·sinωt+(A1-A2)cos(ωt-kx)上式中,由于在换能面上声波的反射率小于1,所以A1>A2,则第二项的行波场始终存在。所以实验中实际合成的声波场由两部分组成,第一部分为驻波场,第二部分为行波场,S1和S2之间的干涉场并不是纯粹的驻波,而是驻波和行波的叠加。
合成声场y也可表示成如下形式:
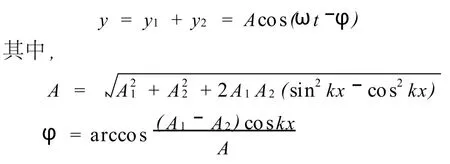
从上式可知,S1和S2之间的任一体元的振动均按余弦规律振动,且各体元的振幅大小随x的变化而变化,其中振幅最大值为A1+A2(kx取π/2的奇数倍),振幅最小值为A1-A2(kx取π的整数倍);各体元的振动初相位大小也随x的变化而变化。
实验中激发换能器的共振频率为40000 Hz,所以声波频率f取40000 Hz,声速v取室温下的标准值342.9m/s,则超声波的波长为0.0085725m。设正向行波振幅A1为1cm,反向行波振幅A2为0.4cm,则由matlab模拟出的两换能器之间合成声场振幅分布如图2和图4所示。

图2 L=λ/2时两换能器之间体元的振幅和初相位分布
从图2中可以看出,当两换能器之间的距离L=0.004286,即为λ/2时,各体元的振幅分布具有部分驻波的特征。两端振幅为最小值0.6cm,即(A1-A2),可以视为波节。中间部分为振幅为最大值1.4cm,即(A1+A2),可以视为波腹;但两波节间各体元的初相位不同,这与驻波的特征不同。
当换能器之间距离L为nλ/2时(取n=7),如图3所示,两换能器之间存在着n+1个波节和n个波腹,两个换能器处为波节;两个相邻的波节或波腹之间对应的距离均为λ/2;任意两个波节内的各体元相位分布规律相同。
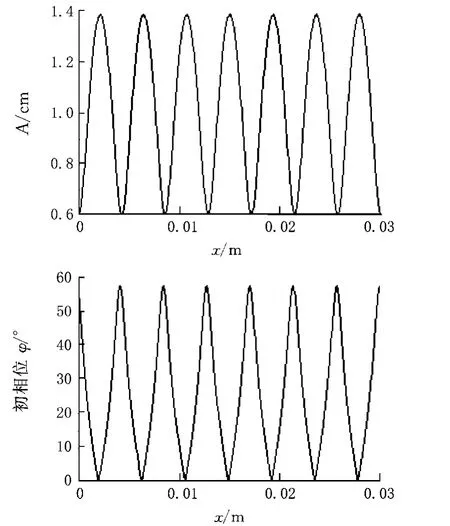
图3 L=7*λ/2时两换能器之间体元的振幅和初相位分布
实验中接收换能器是将声压信号通过压电陶瓷转化为电压信号,所以通过示波器观察到的电信号并不是声波的信号,而S2处的是声压信号。根据S1和S2的之间的干涉声场y的波动方程,推导出声压的波动方程[7-8],得:
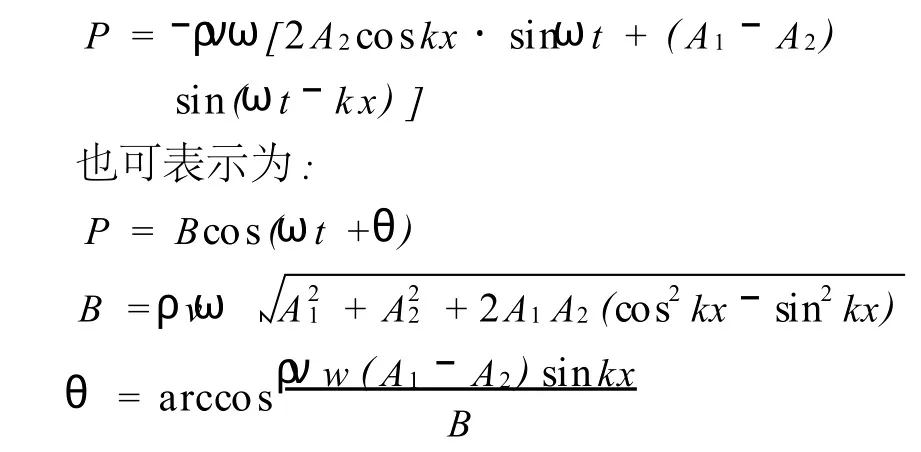
从公式可知,S1和S2之间的声压分布仍有驻波加行波的特征,任一体元的声压波形为余弦规律变化,且体元中当kx取π/2的奇数倍时,振幅最大值为ρ ν ω(A1+A2),当kx取π的整数倍时,振幅为最小值ρ ν ω(A1-A2)。
取正向行波振幅A1为1cm,反向行波振幅A2为 0.4cm,声阻ρ ν取空气中的声阻值 429 Ns/m3,则由matlab模拟出的两换能器之间合成声压幅分布及初相位分布如图4和图5所示。
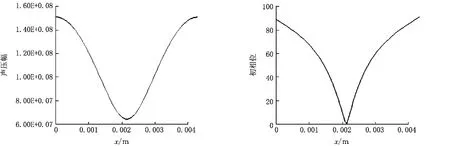
图4 L=λ/2时两换能器之间体元的声压幅和初相位分布

图5 L=7*λ/2时两换能器之间体元的声压幅和初相位分布
图4中,L取λ/2,两换能器之间的声压幅分布和声波的振幅分布刚好相反,两端的声压幅最大,为波腹,中间的声压幅最小,为波节;两波腹间各体元的初相位不同,因此两换能器间的声压场也不是一个纯粹的驻波。
从图5可以看出,当L取nλ/2(n=7)时,两个换能器处的声压处于波腹位置,且两换能器之间存在着n+1个波腹和n个波节,两个相邻的波腹之间对应的距离为λ/2;任意两相邻波节间各体元的初相位分布规律不相同。
根据声压的模拟结果,可以得出如下结论:(1)虽然两换能器的声压场并不是一个纯粹的驻波,但振幅分布仍然具有部分驻波的特征;因此仍然可以根据声压幅转化成的电信号的规律变化来确定声波的波长(2)当L取nλ/2时,接收换能器处的声压幅为最大值,因此从示波器中观察得到的电信号最强。
3 结 论
对驻波法测量声速进行了理论分析,并对结果进行了matlab模拟,给出了直观的模拟结果。结果表明,当两个换能器之间的距离L=nλ/2时,两换能器之间形成声波场和声压场并不是真正的驻波。其中声波场和声压场的振幅分布有部分驻波的波形特点,而声波场和声压场的初相位分布却不符合驻波的特征。
[1]李密丹,马涛.大学物理实验[M].北京:印刷工业出版社,2005:87-92.
[2]任隆良,宋克威,刘金来.驻波法测量声速试验中的非完全驻波[J].物理通报,2002(2):32.
[3]胡险峰.驻波法测量声速实验的讨论[J].物理实验,2007,27(1):3-6.
[4]谭磊,程庆华.驻波法测超声声速实验中的最佳测试距离研究[J].长江大学学报:自然版理工卷,2009,6(4):158-160.
[5]赵新闻.声速测定中驻波共振条件的讨论[J].物理与工程2002,12(3):11-13.
[6]陈殿伟,盖啸尘,王严东.驻波法测定超声波声速实验的探究[J].大学物理实验,2006,19(3):36-39.
[7]漆安慎,杜婵英.力学[M].北京:高等教育出版社,1997.
[8]赵新闻.声速测定中驻波共振条件的讨论[J].物理与工程,2002,12(3):11-13.
Computer Simulation of the Experiment of Measuring the Sound Velocity by Standing Wave Method based on Matlab
ZHANG Chun-mei
(Beijing Institute of Graphic Communication,Beijing 102600)
The paper simulates the distribution of the amplitude and initial phase of the sound field and the sound pressure field based on the synthetic sound field wave equation and the sound pressure wave equation using the matlab language,and analyses the result.
sound velocity;standing wave method;matlab;simulation
O426
A
1007-2934(2010)06-0078-03
2010-06-12
北京印刷学院2010年教学改革项目(22150110032)

