科技进步下人力资本区域经济发展贡献测度研究——以山东省聊城市为例

付景远

(聊城大学管理学院,山东聊城 252059)

科技进步下人力资本区域经济发展贡献测度研究
——以山东省聊城市为例

付景远

(聊城大学管理学院,山东聊城 252059)

聊城市地处山东西部,临近河南、河北,起着辐射和带动鲁西经济发展的作用。如何在科技进步和新一轮经济增长过程中把握有利时机,加大开发人力资本力度,实现区域经济持续快速增长,是迫切需要研究的课题。本文借助经济增长理论,分析科技进步下的人力资本在促进经济增长中的作用,揭示人力资本投资是一个地区经济长期持续增长的源泉。同时,遵循经济发展规律,提出人力资本投资与积累的政策建议。

科技进步;人力资本;经济增长;区域经济

我国从 20世纪 80年代末开始引入人力资本理论,并尝试用这一理论解释我国劳动者素质与经济增长的关系问题以及以人口的质量发展代替人口的数量发展等问题。沈利生、朱运法在其《人力资本与经济增长分析》一书中通过建立大量的分析模型,分析人力资本对经济增长的贡献度,得出了教育投资对人力资本的形成和经济增长有较大的推动作用;王金营在《人力资本与经济增长理论与实证》中以罗默和卢卡斯的新经济增长理论为基础,构建了人力资本外部性模型。

一、科技进步下的人力资本分析模型的发展

(一)哈罗德 -多马模型

哈罗德 -多马模型是 20世纪 40年代分别由英国的罗伊·哈罗德和美国麻省理工学院的埃弗塞·多马提出来的。模型的基本假设是任何经济单位的产出都取决于向该单位投入的资本量。若 Y表示产出,K表示资本存量,于是产出与资本存量的关系是:

其中,k是常数,称为资本—产出比率。为将 (1.1)式转换成表示产出增长情况的公式,ΔY和ΔK表示产出和资本的增量,则 (1.1)式可以写成:

等式两端同时除以 Y,得到:

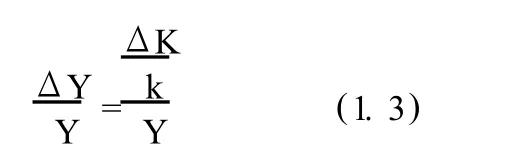
其中,ΔY/Y是产出增长率,用 g来表示。因为对于整个经济来说,资本存量的增量ΔK等于投资 I,而投资 I又等于储蓄 S。因此,可以用 S/Y代替ΔK/Y,S/Y指储蓄在国民生产总值中所占的比重,称为储蓄率,用 s来表示。于是方程(1.3)可转化为:

这就是哈罗德 -多马经济增长模型的基本关系公式。它所表达的基本观点是:用于厂房设备等投资所创造的资本,是经济增长的主要决定因素,储蓄使投资成为可能。

(二)新古典经济增长理论

新古典学派相信市场机制能使资本和劳动力充分吸收,经济会自动走向帕累托最优。为建立增长模型,进行如下假设:

(1)全社会只生产单一商品;

(2)储蓄函数为 S=sY,s为常数,表示储蓄倾向,且 0〈s〈1;

(3)资本—劳动比率和资本—产出比率可以按需要进行调整变化;

(4)随着生产规模的扩大而收益不变或成本不变,但资本或劳动的边际生产率递减;

(5)不存在技术进步,也不存在资本折旧;

(6)劳动力按一个不变的比率 n增长。

假设总生产函数为 Y=F(K,L),其中 K表示总资本量, L表示总劳动量,Y表示总产量。根据假设生产的规模报酬不变,则有λF=λY=F(λK,λL),令,则得到,记为,则可以把生产函数表示为:

在上述假设条件下,索洛推导出新古典增长模型的基本方程:

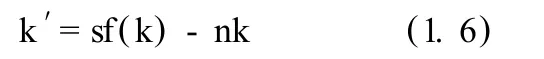
上式中 k’表示资本存量变化率,它衡量了每个劳动力拥有的资本增加量,通常被称为资本深化;f(k)表示人均收入表示人均储蓄量或投资量 (假定储蓄等于投资);nk表示当劳动力以速率 n增长时,为保持资本劳动比不变所需的投资量。假定技术进步是劳动增强型的并引进基本模型,技术进步率为 g。由于哈罗德中性的技术进步相当于劳动力规模的增加,因此这种技术进步形式很容易被纳入 (1.6)模型,这时新古典经济增长理论的基本方程变为:

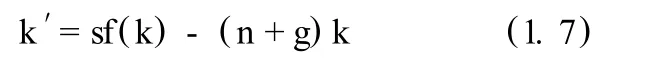
新古典增长理论将动态一般均衡分析方法引入经济增长的研究中,为后来相关研究提供了分析工具。它说明发展中国家在增加储蓄和引进外资时不应仅看重资本存量的积累,而更应关注资本质量的提高,它强调收入增长的源泉是技术进步。

(三)新增长理论

新增长理论以美国经济学家保罗·罗默 1986年的论文《递增收益和经济增长》为标志,它把技术进步看作资本投资增加的结果,资本是增长模型中的关键变量,技术进步就成为内生因素。在模型中技术是由经济体内生得到的,它与资本和劳动力共同促进了经济的增长。假设生产过程中劳动力质量得到提高,并需要企业的投资,同时产生企业资本存量、知识存量的增加。所以,劳动力质量要素的增长率与总的资本存量的增长率成比例。根据上面的假设,可得劳动力质量(Lq)与资本存量 (K)的函数关系,即:

式中,φ为资本对劳动力质量的影响系数,在资本存量中,投入到教育和研发等方面的资本比重越高,φ越大。

在新增长理论中,内尔森 (Nelson)在他的经济增长模型中首先提到了资本质量的概念,他认为新资本投资促进的技术改进将增加经济增长率对于资本要素增长的弹性。他还提出了质量权数的概念,认为新投入资本在经济增长中的贡献要大于以前投入的资本,其质量权数较大。新增长模型参考了内尔森的思路,加入了资本质量要素。模型假设新投入的资本要比以前投入的资本有更高的质量,资本的质量与资本存量的平均使用时间成反比。

综合上面两点,在新古典经济增长模型中引入劳动力质量要素和资本质量要素,可构建柯布 -道格拉斯生产函数模型如下:

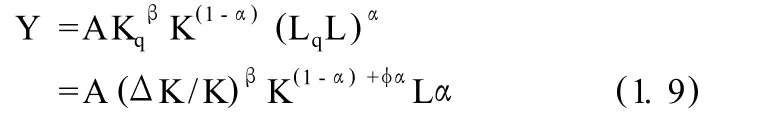
上式中,Y表示总产出;A表示中性技术变化;Kq表示资本质量;K表示资本数量;Lq表示劳动力质量。L表示劳动力数量;α表示劳动力收入在国民收入中所占的相对份额;β表示资本质量对产出的影响系数;φ为资本存量对劳动力质量的影响系数。

这一模型强调科技进步可以提高投资的收益,投资又会引起知识的积累,知识增加加快科技进步的进程,在这种正反馈中,经济增长产生良性循环,从而长期稳定地提高经济增长率。新增长理论解释了技术进步和长期增长的源泉以及发达国家与发展中国家的增长率和收入水平差距不断扩大的原因。从理论上更为鲜明地肯定了人力资本投资、科学技术研究、发明与创新、开放经济等对经济发展的决定性意义。

二、区域经济发展中人力资本存量测度

人力资本存量是指一个区域劳动力群体具有的人力资本整合,人力资本的度量从不同的角度考虑有着不同的度量方法。为分析简洁明了起见,本文将采用劳动力平均受教育年限表征人力资本水平。受教育年限法是指将劳动力分类,然后按照不同劳动力的人力资本特质对其进行加权求和,即得到总的人力资本存量。用劳动力的受教育程度或年限代表劳动力的人力资本存量不仅简明扼要,数据获得的可能性和精确性强,而且受教育年限与接受教育或培训的劳动力人力资本投资成本有较强的正相关性,它排除了用货币计算人力资本投资成本的价格因素影响①高明,姜学民,任龙:《山东省人力资本与经济增长的实证分析》,《山东经济》,2007年第 2期。。

在计算聊城市人力资本水平时运用 2000年的第五次人口普查的数据,首先计算 2000年 15岁以上人口的平均受教育程度,然后再计算全社会人均受教育程度 (6岁及以上),最后,用前者除以后者得到 15岁以上人口的受教育水平占全社会人口受教育水平的比重。假设人口结构基本保持不变,那么可以认为这个系数在这二十八年保持不变,利用这个系数可以推断出其他年份的 15岁以上人口平均受教育年限。将这个比例系数应用到 1980和 1990年,计算出这些年份的 15岁及以上人口的平均受教育年限②韩泽瑜,纪美霞:《山东省人力资本的核算及其对区域经济增长的实证研究》,《工业技术经济》,2006年第 25卷第 12期。。

根据研究对象的实际情况,用人均受教育年限表示人力资本水平,并计算聊城市的人力资本存量,其计算公式为:

其中M为人力资本的平均受教育年限,Xi为第 i类学历的人力资本数量,Ti为第 i类学历的受教育年数。有关受教育程度的分类,将教育层次划分为文盲半文盲、小学、初中、高中、大学专科和大学本科及以上六类,各学历受教育年限依次界定为 2年、6年、3年、3年、2.5年和 4年,同级教育中成人教育与普通教育和自学考试取得的学历是同质的。

表 2.1 聊城市主要年份 6岁和 15岁以上人均受教育年限 单位:年

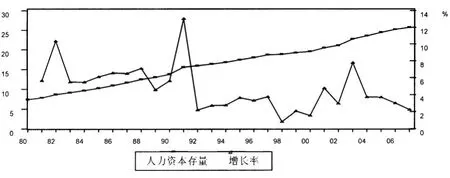
图 2.1 聊城市人力资本存量及其增长率的变化图

根据表 2.1中的三组数据进行直线回归,前推至 1980年,得到 1980年至 1990年每年社会平均受教育年限。同理,把 1990年和 2000年的数据进行直线回归可以推算出从1990年至 2007年历年的社会平均受教育年限。由于统计数据可得性的限制,结合本文研究的目的,采用这种方法可以提供基本的参考。各年的 15岁以上人口的平均受教育年限分别乘上各年的劳动力人数即为各年的人力资本存量。(结果见图 2.1和表 2.2)

由图 2.1和表 2.2可知:

第一,聊城市的人力资本存量随时间的推移呈递增趋势。这不仅与人力资本的可积累性有关,还与人口数量的不断增加和人均受教育水平的提高有直接的关系。从 1980年至 2007年,聊城市的人力资本存量由 1980年的 743.97(万人年)增长到 2007年的 2574.18(万人年),增长了 3.46倍,年平均增加量达 65.36(万人年)。

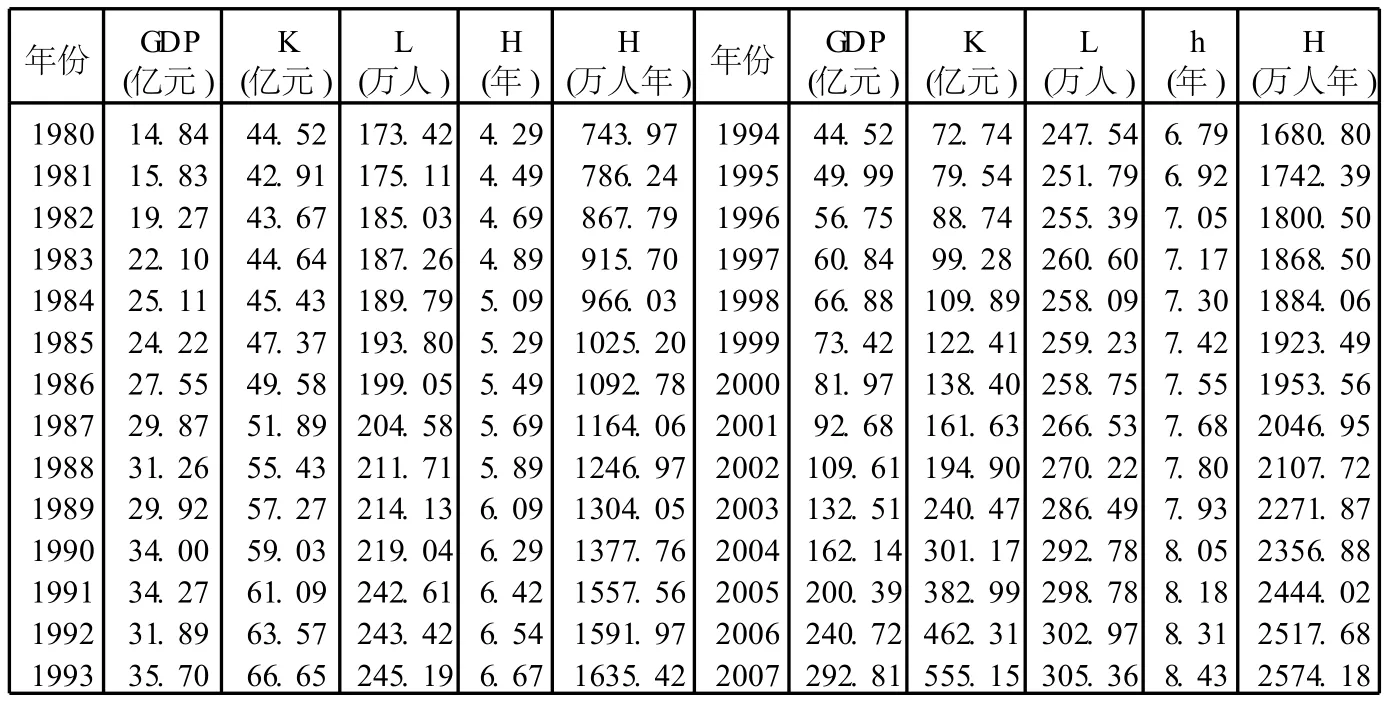
表 2.2 聊城市国内生产总值、物质资本存量、人力资本水平、人力资本存量、劳动力人数等指标数据概况(1980-2007)

第二,聊城市人力资本存量大体是先增后减,呈三高一低的变化趋势。三个波峰和一个波谷分别出现在 1982年、1991年、1998年和 2003年。第一个波峰出现的原因是:中国自 1977年恢复高考制度以来,许多学生有机会上大学继续深造,这极大地促进了人力资本水平的提高,人力资本存量随之快速增加。由于聊城市劳动力人数的快速增加,导致人力资本存量增加,出现了第二次波峰。第三次波峰的出现是由于高校的不断扩招,大学在校生的数量剧增,无形之中提高了人力资本水平,进而加速了人力资本存量的增加。

三、科技进步下的人力资本贡献分析

(一)基础模型借鉴

1.人力资本有效劳动模型

在模型中将人力资本内生为劳动力的有效劳动,而不考虑人力资本在生产中具有的“溢出效应”。

公式中 Yt为聊城市的国内生产总值,At为考虑物质资本存量和人力资本存量的综合要素生产率,Kt为聊城市物质资本存量,Ht为聊城市人力资本存量,α为物质资本产出弹性,β为人力资本存量产出弹性,μ是随机干扰因素。对 4.1式两边同时取自然对数并变形可得:

α、β可利用上面的方程进行线性回归求得。

同时可以得到经济增长方程:

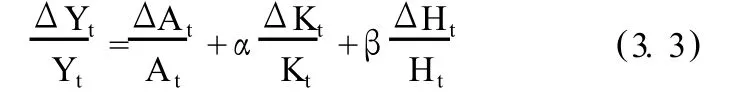
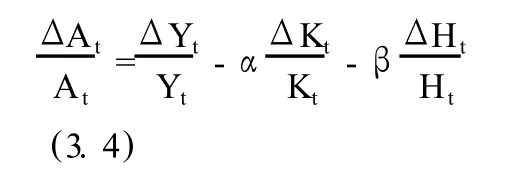
2.人力资本外部性模型

人力资本外部性模型的形式为:

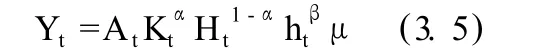
上式中 Yt为第 t年聊城市的国内生产总值,At为第 t年考虑物质资本存量和人力资本存量及人力资本水平的综合要素生产率,Kt表示第 t年聊城市物质资本存量,Ht表示第 t年聊城市人力资本存量,ht表示第 t年聊城市就业人员的平均受教育年限,即人力资本水平,μ是随机干扰因素,α为物质资本产出弹性,β为人力资本水平产出弹性。对上式两边同时取自然对数并变形可得:

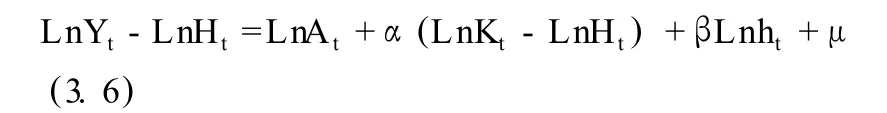
同时可以得到经济增长方程:

卢卡斯认为人力资本积累是长期经济增长的源泉,他的人力资本外部性模型不仅充分考虑了人力资本的生产功能,而且充分考虑到人力资本对其他非人力资本要素的外部性作用,真实反映了产出与要素投入的函数关系,有利于准确判断人力资本在经济增长中的作用。

(二)科技进步下区域经济增长分析

根据人力资本的有效劳动模型和外部性模型的要求,利用表 2-2的 GDP、物质资本和人力资本的数据,我们给出各种数据的自然对数值。如表 3.1所示:

表 3.1 聊城市经济增长及各要素数据的自然对数值(1980-2007)

利用表 3.1的数据,应用 SPSS统计软件对公式 3.2和 3.6进行回归分析,得到以下结果:

第一、人力资本有效劳动模型估计检验结果。相关系数 R=0.995,R2= 0.991,经调整的 R2=0.990,估计标准误差为 0.08368,以上数据表明因变量与自变量之间存在极为显著的线性相关关系。F值为 1306.721,F分布的显著性概率为 0.000,即检验假设成立的概率等于 0.000,从而说明回归效果极为显著。该模型整体通过 F检验和 T检验,且显著水平较高,样本观测值的拟合程度非常好。表明聊城市的国内生产总值和物质资本与人力资本之间的关系符合人力资本有效劳动模型,将标准化系数代入方程 3.1得到有效劳动模型:

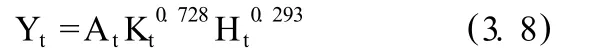
从上面的模型可以看出物质资本的产出弹性要高于人力资本的产出弹性。这说明聊城市的经济增长主要依靠物质资本的拉动。

第二、人力资本外部性模型检测结果。相关系数 R= 0.989,R2=0.977,经调整的 R2=0.975,估计标准误差为0.07825,以上数据表明因变量与自变量之间存在极为显著的线性相关关系。F值为 538.472,F分布的显著性概率为0.000,即检验假设成立的概率等于 0.000,从而说明回归效果极为显著。该模型整体通过 F检验和 T检验,且显著水平较高,样本观测值的拟合程度好。这表明聊城市的国内生产总值与物质资本、人力资本存量和人力资本水平之间的关系符合人力资本外部性模型。这表明在聊城的经济增长中,人力资本水平具有明显的外部性且有较高的产出弹性,但物质资本仍是起主导作用的因素,科技进步下的人力资本水平外部性要素贡献率偏低。

为更准确的得出结论,我们进一步利用国内生产总值、物质资本、人力资本水平和人力资本存量的各年增长率和分阶段的年均增长率,并使用 3.7式计算得到表 3.2。

根据人力资本外部性模型估算各个投入要素贡献率,得以下结论:

从模型看出,物质资本有着高出人力资本的产出弹性,表明多年来经济增长的主要拉动力是物质资本投入。这隐含聊城市实际生产过程中在科技进步得不到保障的时候物质资本投入出现了报酬递减。从增长率方面来看,物质资本存量的迅速积累对聊城市的经济高速增长起了主导作用,经济增长仍然是以“粗放型”(即高资本拉动型)增长方式为主。

综合要素生产率对聊城市经济增长的贡献整体偏低。说明技术创新在经济增长过程中处于非主导地位,经济增长没进入创新驱动阶段。一个经济体只有伴着科技进步才可能持续增长,科技水平的不断提高能够克服资本积累的报酬递减而提高劳动生产率。若没有科技进步,资本积累达到一定程度后,经济反而会出现衰退。

表 3.2 人力资本外部性模型下聊城市各时期生产要素对经济增长的贡献率 单位:%

四、对策与建议

实证分析可以看出,由于人力资本水平具有明显的外部性作用且有较高的产出弹性,科技进步下的人力资本可以作为区域经济增长的主要支撑。从提高人力资本贡献率角度提出以下政策建议:

第一、优化政府资金投放结构,加大教育投入。在经济欠发达地区必须加速改善教育投资观念,在政府的财政预算内加大对教育的投入,实现财政性教育经费占国民生产总值的比重达到较高的水平。

第二、优化人力资本投资结构,发展多形式教育。聊城市目前基础教育薄弱,高等教育与需求脱节,职业教育尚不发达,应鼓励投资主体加大人力资本投资。

第三、建立和完善人力资本市场体系,促进人才的有效流动性。通过完善人才市场网络最大限度的使人才与岗位合理配置,减少人才的闲置和浪费。要实施人力资本“走出去”和“引进来”的政策,加强人力资本的市际、省际和国际交流。

第四、倡导创新,培育创新型人才,提高人力资本的综合使用效率。鼓励科研创新为区域经济发展、社会进步提供智力支持和科技保证。

[1]苏雪串,徐大佑:《论人力资本与经济发展》,《云南财贸学院学报》,1999年第 6期,第 25-28页。

[2]陈理飞,夏建伟:《江苏省科技投入与经济增长的动态均衡分析》,《科技管理与研究》,2009年第 5期,第 228-230页。

[3]赵曙明,陈天渔:《经济增长方式转型与人力资本投资》,《江苏社会科学》,1998年第 1期,第 43-48页。

[4]刘迎秋:《论人力资本投资及其对中国经济成长的意义》,《管理世界》,1997年第 3期,第 55-63页。

[5]赵曦:《人力资本理论与反贫困问题研究》,《改革与战略》,1997年第 4期,第 9-13页。

[6]吴敏,李丹:《四川省高新技术产业贡献度实证分析》,《科技进步与对策》,2009年第 14期,第 40-42页。

[7]王金营:《人力资本与经济增长理论与实证》,北京:中国财政经济出版社,2001年版。

[8]聊城市统计局:《聊城统计年鉴 (1980-2007)》。

付景远(1963-),男,聊城大学管理学院副教授,硕士研究生导师。

F127

A

1003-8353(2010)06-0137-04

[责任编辑:王成利 ]