一种基于 RSSI的几何位置定位新算法*

郑 晨,王 玫

(桂林电子科技大学信息与通信学院,广西桂林 541004)

ZHENGChen,WANG Mei*

(Department of Communication and Information System,Guilin University of Electronic Technology,Guilin Guangxi 541004,China)

随着通信技术、嵌入式计算技术和传感器技术的日益发展和成熟,具有感知能力、计算能力和通信能力的微型传感器开始在世界范围内出现。1999年提出的“物联网”概念,即通过射频识别(RFID)、红外感应器、全球定位系统(GPS)、激光扫描器等信息传感设备,按约定的协议,把任何物品与互联网连接起来,进行信息交换和通讯,以实现智能化识别、定位、跟踪和监控管理的一种网络。“物联网”用途广泛,遍及智能交通、环境保护、公共安全、工业监测等多个领域。而“物联网”的主要组成部分就是无线传感器,通过部署大量的传感器节点至目标区域,可以在广泛的应用领域内实现复杂的大范围监测和追踪任务。在室内目标定位和跟踪的应用中,无线传感器正好弥补了 GPS在室内难以获得位置信息的弊端,得到实时位置信息[1-3]。

近年来,基于无线传感器网络(WSN,Wireless Sensor Networks)的室内定位技术迅速发展,先后出现了 RADAR[4]、Cricket[5]、SpotON[6]、Nibble[7]等定位系统,这些定位系统通常采用接收信号强度指示(RSSI,Received Signal Strength Indictor),和信号传播时间差(TDOA,Time Difference of Arrival)[8]技术。在 TDOA技术中,传感器节点需要集成超声波收发装置,不但增大了节点尺寸,提高了成本和能耗,而且传播距离短、穿透性差。采用 RSSI技术的定位方法,在信标节点广播自身坐标的同时可完成 RSSI的测量,RSSI利用已知发射信号强度,接收节点根据收到的信号强度,计算信号在传播过程中的损耗,使用理论或经验的信号传播模型将传播损耗转化为距离。节点无需额外的硬件装置,功耗低,成本低,能满足大规模的应用要求,已在许多项目中得以应用。

目前,基于 RSSI无线传感器网络定位算法有多种提高定位精度的方法。文献[9]用加权质心算法通过信标节点对未知节点的不同影响力来确定加权因子,提高定位精度,但是此算法很大程度的依赖信号传播模型中的路径损耗指数。文献[10]采用多次测量求平均的统计滤波的方法,消除环境干扰等偶然因素产生的静态误差,不过该方法对因节点硬件失效或障碍物阻挡等产生的测距误差并不是很有效。文献[4]和[11]运用插值法以减少测量次数,这些技术利用空间信息或经典的传播模型在一些信标节点中插值以提高定位精度,但是在动态的环境中这些方法难以获得准确的信息。

不同于上述定位算法,本文采用圆的几何力量线—根轴理论,提出一种适合于室内环境的定位算法。该算法能够对未知节点进行快速定位,并具有较小的计算开销,定位精度高,环境干扰鲁棒性强。

1 根轴定位算法描述

1.1 理论推导

根轴[12]在平面上任给两个不同心的圆,则对两圆圆幂相等的点的集合是一条直线,这条直线成为两圆的根轴。根轴反应了一个点与圆的相对距离关系。

圆幂[12]假设平面上有一点 P,有一圆 O,其半径为 R,则 OP2-OR2即为 P点到圆 O的幂。所以,圆外的点对圆的幂为正,圆内的点对圆的幂为负,圆上的点对圆的幂为 0。

相关定理

平面上任意两圆的根轴垂直于他们的连心线。

若两圆相交,则两圆的根轴为其公共弦所在直线。

若两圆相切,则两圆的根轴为其公切线。

图 1 三种圆的位置关系所产生的根轴

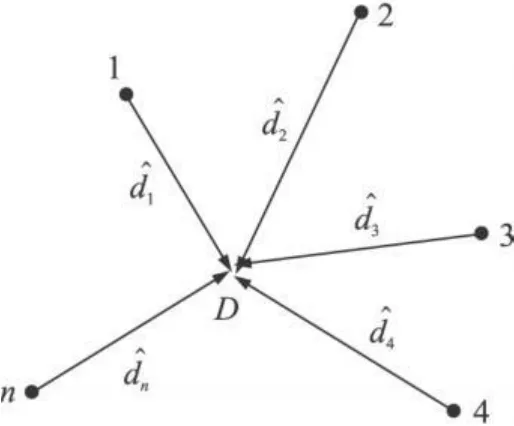
图 2 极大似然估计法图示

但在实际情况中,由于多径、绕射、障碍物等因素,基于 RSSI的测距不会为精确值,所以测量距离为半径的 n个圆不会交于一点,所以,我们采用圆的根轴定位。已知 n(n≥3)个信标节点坐标以及他们到未知节点的距离,就会产生 n个圆,其方程为：

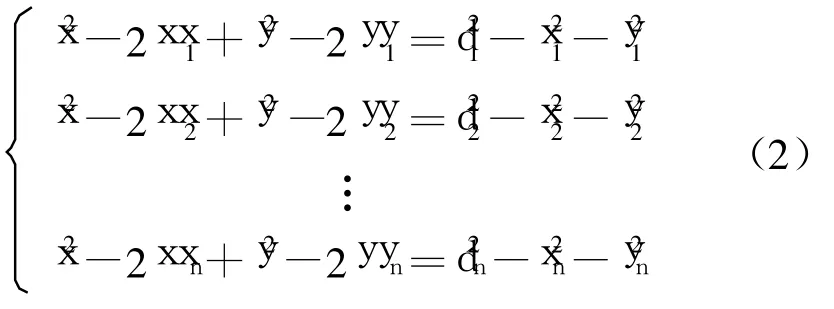
假设 n=3,则有 (1,2)、(1,3)、(2,3)三条根轴。当有 n个信标节点时,则将式(2)的第一个方程分别减去第二个直到最后一个方程,可得 C2n=n(n-1)/2条根轴方程：

由这 n(n-1)/2个线性方程可以得出矩阵方程

其中 A为 n(n-1)/2行,2列的矩阵,b为 n(n-1)/2列的向量。

如果所有的根轴都交于一点,那么线性方程组(3)只有唯一解。但一般情况式(4)为超定系统,这时它的最小二乘解(˜x,˜y),就是使其到每条根轴的距离的平方和最小的点,为 n(n-1)/2条根轴的最小二乘解,即可求得未知节点的估计位置。图 3中我们可以看到矩阵方程(4)的最小二乘解的具体情况。通常方程(4)的解为：

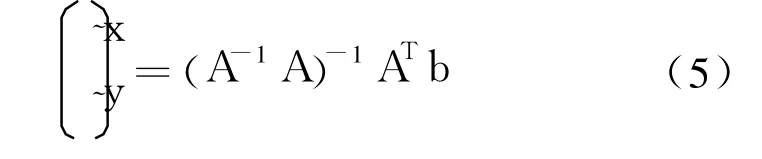
1.2 RSSI测距模型

无线电传播路径损耗对于 RSSI定位算法的定位精度有很大影响。常用的传播路径损耗模型有自由空间传播模型;对数距离路径损耗模型;哈它模型;对数—常态分布模型。本文采用自由空间传播模型和对数—常态分布模型用于分析和仿真。自由空间无线电传播路径损耗模型如下[1]：

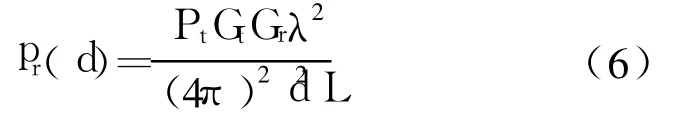
其中,Pt为信源的发射功率 W,Gt为发射天线增益,Gr为接受天线增益,λ为信号波长,d为距信源的距离 m,L为与传播无关的系统损耗因子(不小于1)。

在实际应用环境中,由于多径、绕射、障碍物等因素,无线电传播路径损耗与理论值相比有些变化。下述对数—常态模型将更加合理,下式可用于计算节点收到信标信息时的路径损耗。其统计模型如下[13]：

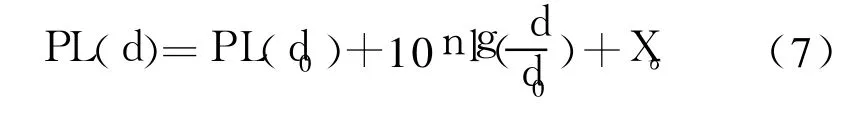
其中,PL(d)为经过距离 d后的路径损耗,单位为 dB;Xσ为均值为 0的高斯分布随机变量,其标准差范围为 4—10。n为路径损耗因子,在室内环境下n的范围在 2—4之间。取 d=1 m,代入式 (6),可得到 PL(d0)的值。所以,各未知节点接收到信标节点信号时的信号强度为：

其中 RSSI为加上高斯随机变量的接收功率,以此来模拟未知节点接收功率的测量值,单位为 W,Pt为发射功率。将(8)代入式(7)可得从发射点到接收点的估计距离。

1.3 根轴定位算法描述

传感器网络基于距离 RSSI定位算法在室内环境下定位精度不高,针对 RSSI算法的不足,根据根轴定理,提出了基于根轴的定位算法。

基于距离的 RSSI定位算法为传统算法,所以将根轴算法与传统算法比较其优越性。首先对基于RSSI距离定位传统算法的定位过程描述如下：

①信标节点周期发送自身信息 节点 ID、自身位置信息。

②未知节点收到多个信标节点的 RSSI值,根据信道模型计算节点间的距离。

基于 RSSI加权质心法：任取 3个信标节点,对其求加权质心可得未知节点的位置估计。

基于 RSSI极大似然估计法：对所有的信标节点用极大似然估计法取得未知节点的位置估计。

由于信标节点对未知节点位置都有影响力,RSSI越大的信标节点,影响力越大,对节点位置有更大的决定权。所以,本文采用基于根轴定位算法的两种方法与传统算法进行性能对比,算法描述如下：

①信标节点周期发送自身信息：节点 ID、自身位置信息。

②未知节点收到多个信标节点的 RSSI值后根据信道模型计算节点间的距离。

方法①：将 RSSI值从大到小排列,取前三个信标节点两两组合取根轴求最小二乘解即为未知节点位置估计。

方法②：用所有的信标节点取其根轴,用极大似然估计法得出未知节点的位置估计。

2 仿真结果及性能分析

为验证本文算法的可行性,在 Windows平台上利用 MATLAB语言实现。信标节点和未知节点随机分布,每个未知节点都可以全部收到信标节点的信息。信标节点周期的发送自身信息。路径损耗因子 n=2,参考距离 d0=1 m。

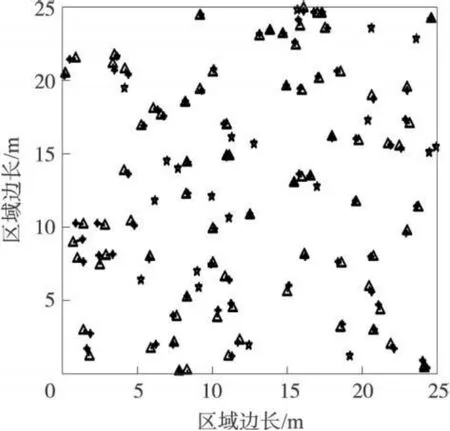
图 4 根轴定位算法效果

图 5显示了在 25 m×25 m的环境中,节点数目为 100个的条件下不同信标数目下两种方法的定位性能。图 5(a)说明了当信标节点从 4个增加到 12个时,根轴定位算法的平均定位误差提高的幅度较大,当信标节点数(≥12个)时,就能获得较高的定位精度,进一步增加信标数目,并不能显著提高未知节点的定位精度。其中,根轴定位算法较加权质心算法获得定位精度高 50%。图 5(b)中,同为基于极大似然估计算法,当信标节点数很少时(4个),两者几乎重合,当信标数逐渐增大时两者才可分辨出来。而根轴极大似然定位较RSSI极大似然定位精度高 18%。但同为根轴估计算法,基于极大似然根轴估计定位算法付出了更多的计算开销,换取了定位性能的提升。

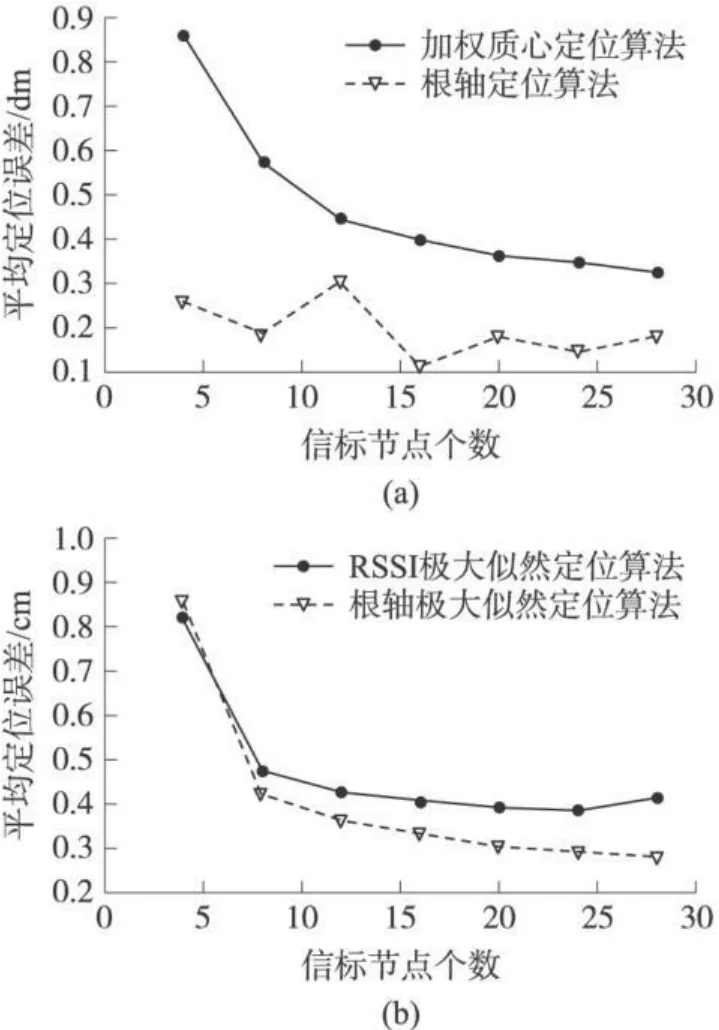
图 5 不同信标数目下的定位性能

图 6显示了 100个节点中 4个信标节点数不变,区域边长从10 m增加到 45 m时,平均定位误差随着节点密度的减小而增大。但从图 6(a)可以看出,根轴定位算法受节点密度的影响并不是很大,平均定位误差趋于稳定,较加权质心提高了 67%。而图 6(b)基于极大似然的根轴定位算法由于通过所有的信标节点引入限制条件,所以受节点密度对影响较大。定位精度较 RSSI极大似然定位并无很大提高,但由此可知在实际应用中,可以通过合理设置信标节点的位置使它们在统计意义上与可能的未知节点间的距离最小,从而达到提高定位精度的目的。

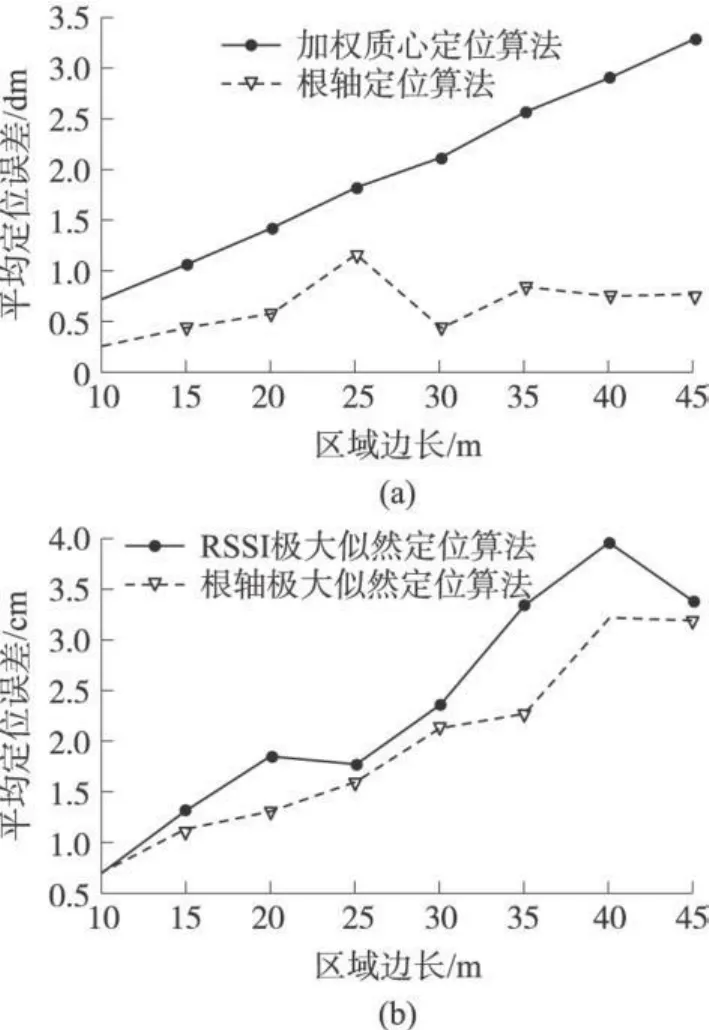
图6 不同节点密度下的定位性能

3 结论及展望

本文在对 RSSI测距模型和基于 RSSI测距定位算法分析和研究的基础上,提出了基于几何力量线——圆的根轴定位算法,将最大似然估计法应用到根轴定位算法中,改进了传统的基于距离定位的三边测量估计算法,提高了定位精度。实验结果表明,改进后的定位算法在计算通信量略微增加的基础上明显提高了定位精度和系统稳定性,算法性能优于其他算法,能够运用到实际的室内环境定位中。本文下一步的工作将探讨和研究在不同信道环境下的根轴定位算法的性能以及利用UWB信号特性,设计面向测距和定位的超宽带传感器网络定位系统。

[1] Santiago Mazuelas,Alfonso Bahillo,Evaristo J Abril,et al.Robust Indoor Positioning Provided by Real-Time RSSI Values in Un-modified WLAN Networks[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(5)：821-831.

[2]Liu B C,Lin K H,Wu J C,et al.Anlaysis of Hyperbolic and Circular Positioning Algorithms Using Stationary Signal Strength Difference Measurements in Wireless Communications[J].IEEE Trans.Veh.Technol,2006,55(2)：499-509.

[3]Heikki L,Suvi J,Jaakko L,et al.Experimental Evaluation of Location Methods Based on Signal-Strength Measurements[J].IEEE Trans.Veh.Technol,2007,56(1)：287-296.

[4]Bahl P,Padmanabhan V N.Radar：An In-Building Rf-Based User Location and Tracking System[C]//Proceedings of the IEEE INFOCOM 2000.Tel-Aviv,lsrael,2000,775-784.

[5]Priyantha N B,Chakraborty A,Balakrishnan H,et al.The Crcket Location-Supper System[C]//Proceedings of the 6th Annual Int'l Conf.on Mobile Computing and Networking.Boston,MA,USA,2000,32-43.

[6]Hightower J,Boriello G,Want R,et al.Spoton：an Indoor 3d Location Sensing Techology Based on Rf Signal Strength[R].Technical Report UWCSE 2000-02-02,Seattle：Department of Computer Science an Engineering,University of Washingon,2000.

[7]Castro P,Chiu P,Kremenek T,et al,A Probabilistic Room Location Dervice for Eireless Networked Rnvironment[C]//Proceedings of Ubicomp 2001.Atlanta,Georgia,USA,2001,18-34.

[8] 孙利民,李建中,陈渝,等.无线传感器网络[M].北京：清华大学出版社,2005,138.

[9] 陈维克,李文峰,首晰,等.基于 RSSI的无线传感器网络加权质心定位算法[J].武汉理工大学学报,2006,30(2)：256-268.

[10]Kwon Y,Mechitov K,Sundresh S,et al.Resilient Localization for Sensor Networks in Outdoor Environments[C]//Proceedings of the 25 th International Conference on Distributed Computing Systems(ICDCS).Columbus,Ohio,USA,2005,643-652.

[11]Z Xiang,SSong,JChen,et al.A wireless LAN-Based Indoor Positioning Technology[C]//IBM J.Res.Dev.2004,617-626.

[12]H SM Coxter.Introduction to Geometry[M].New York：Wiley,1969,86.

[13]吴迪,李仁发,梁华林,等.超宽带传感器网络室内信道建模与定位算法研究[J].系统仿真学报,2009,21(5)：1353-1357.