基于 FPGA的 sinc插值算法的研究和实现

何 斌,张志敏

(1.中国科学院电子学研究所,北京 100190;2.中国科学院研究生院,北京 100039)

1.Instituteof Electronics of Chinese Academy of Sciences,Beijing 100190,China;

2.Graduate University of Chinese Academy of Sciences,Beijing 100039,China

传统的多带宽合成孔径雷达(Synthetic Aperture Radar,SAR)系统的数据预处理模块通常存在模拟接收机滤波器组设计复杂和多种采样时钟同步困难等缺点。针对这些缺点,最容易想到的数字解决方案是采用 1个高采样频率时钟,使其为各输入信号采样时钟的整数倍,这样获取高数据率信号后,通过整数倍降采样即可获得系统要求的各种数据率信号,如图 1(a)所示。该方案中虽然仅有 1个采样时钟,但也带来了新的问题,即采样率过高。以200 MHz,300 MHz,400MHz和 500 MHz带宽的线性调频信号为例,按照 1.2倍的过采样率[1],各采样频率分别为 240 MHz,360 MHz,480 MHz和 600MHz,则 ADC的采样率要取它们的公倍数,至少要达到7 200 MHz,这会给器件选择和电路实现都带来很大困难[2-3],并且对数字滤波器的处理速度要求也非常高。

针对上述问题,本文提出一种新的多带宽 SAR系统数字处理方案,如图 1(b)所示。该方案采用各带宽信号采样频率中的最高的一个作为系统采样时钟,如上例中取 600 MHz,通过插值的方法产生其它各采样频率的信号的同时,还直接实现了数据的降采样,节约了硬件资源。该方案仅采用了 1个模拟接收机滤波器和1个采样时钟,并且采样时钟频率也不比传统方法高,同时也解决了传统方案中存在的多种采样时钟同步困难等问题。方案中的插值运算会对数据实时处理提出较高要求,通常情况下,一个 8点的加权 sinc函数插值比较适合 SAR数据处理[1,3]。

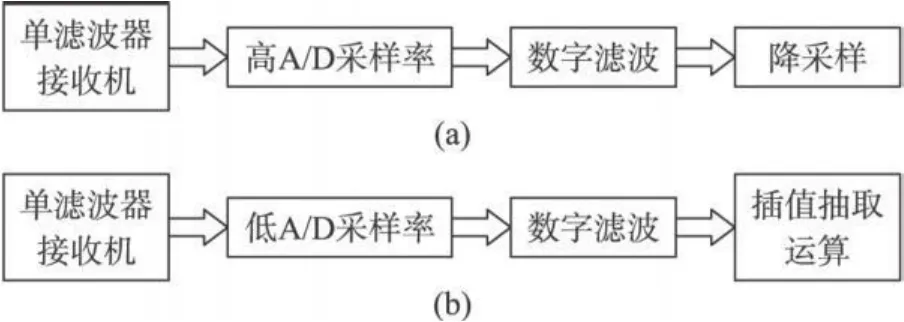
图 1 多带宽SAR系统数据预处理解决方案框图

1 Sinc插值原理

设有函数 f(x),采样定理表明,在满足以下两个条件时,就可以从 f(x)的等间隔离散样本中无失真的重建原始信号：

(1)信号是带限的,即信号的最高频率有界;

(2)采样频率满足奈奎斯特采样率。实信号的采样率必须大于信号最高频率的两倍,复信号的采样率必须大于信号的带宽。

当满足以上条件时,在基带信号下,其重建方程为：

上式可以看成是 fd(i)与 sinc(i)的卷积,其卷积核为

fd(i)是 f(x)在 x=i时的采样值。

式(1)可以理解为所有输入样本的加权叠加,由此式就可以计算出任意点处 f(x)函数值。为精确计算某一点上的 f(x)需要覆盖无限多个点。实际上这是无法做到的,而且使用大量数据点会使插值非常耗时,但精度提高的却很小[4]。计算表明,核值随着与x的间隔增大而降低,这意味着可以在不过度损失精度的同时对卷积核进行截断。在现有的计算资源下,一个 8点的加权 sinc函数比较适合数据处理[3]。

当使用截断后的 sinc函数对存在陡峭边缘的函数进行插值时,会出现一种称为 Gibbs效应的振铃现象。为减小这种影响,应对插值核进行加窗锐化,通常加 Kaiser窗的处理效果比较理想,如图 2。对于加窗后的插值核,需要进行归一化处理,使其增益单位化,否则采样点上的权值和不再等于 1,并且不同插值点之间会出现较大误差。

图 2 加 Kaiser窗前后 sinc函数频谱比较

用 FPGA实现 sinc插值算法时,为提高计算效率,可以将升采样后的插值核存储在表格中,使用查找表实现sinc插值因子的选择[5],这样就无需对每个插值点计算sinc函数、窗系数和归一化因子,而只需使用最接近移动位置处的表格系数,从而大大减小了硬件资源开销。为减小误差,表格系数通常量化为 16位有符号数[6]。图3给出了计算插值核表格的示意图。

图3 插值核表格计算示意图

插值核表格计算时采用 8点的 sinc函数,量化位移为采样点的 1/16,则表格系数共有 16行,每行8个系数。图 3中,实线以 0为中心,虚线以 11/16为中心,分别计算 -3～+4数据点处的权值,即得平移零个采样点(第 1行)和平移 11/16个采样点(第 12行)的表格系数。

2 sinc插值算法的 FPGA实现

sinc插值算法实现的流程图如图 4。实时的处理 SAR数据时,根据 SAR信号产生的特点,必需先将距离向数据缓存到 FPGA内部的 BlockRAM中,以便后续的插值处理。

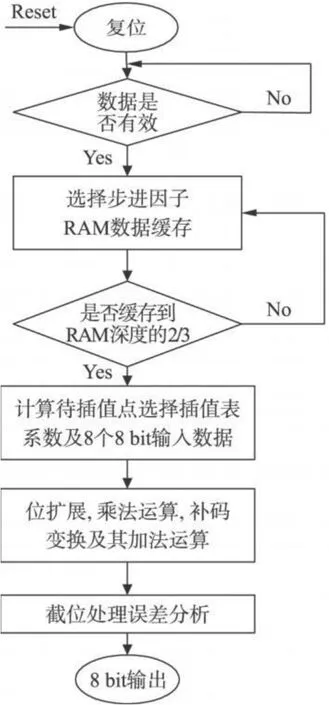
图 4 sinc插值算法实现流程

当FPGA进入复位状态后,便开始检测数据有效标志信号。一旦数据有效标志信号为高电平,就将数据缓存到 FPGA内部的BlockRAM中,并根据带宽控制字选择步进因子。BlockRAM缓存深度由 FPGA的处理能力和实际需要决定,本文中的BlockRAM数据缓存深度为 16384[7-8].由于步进因子值大于 1,且待插值点由步进因子累加得到,为保证输出数据的连续性和节约硬件资源,插值操作必需等 SAR数据缓存到一定数量时才能开始进行。等待深度设置的原则是SAR数据必需在计算最后一个插值点前完成缓存操作,本文中选择等待深度为BlockRAM数据缓存深度的 2/3大小。

为减小插值误差,选择合适的插值表系数非常重要,其选择原则如下：用待插值点的小数部分乘以16,然后将得到的数值四舍五入即可得到所要选择的插值表系数的行数和对应行中的系数。

采用 8点的 sinc函数进行插值运算时,根据待插值点的位置,按照时钟节拍选择所需的 8个数据,其选取原则是以待插值点的整数部分为中心,选择其前三个点和其后四个点。但开始的几个待插值点,有可能取不到其前面全部的三个点,此时将取不到的数据点全部置零,如图 5;最后几个待插值点有可能取不到其后全部的四个点,此时也要将取不到的数据点全部置零,如图 6。

图 5 开始点插值数据的选择

图 6 结束点插值数据的选择

完成乘法运算后,要对数据进行位扩展和补码变换。因为用补码进行加减运算时,符号位直接参与运算,否则运算时必需判断符号位,这就使整个电路逻辑设计复杂化,也必然增加硬件资源开销,影响计算效率。然后对补码变换后的数据进行三级流水线加法运算[9],最后将累加结果进行补码反变换即可得出插值中间结果。由于进行了位扩展,累加结果并不是实际的插值结果,只能取其中的某些位作为实际数据输出。通常把累加结果的最高位作为输出数据的符号位,取其后面的第 16到 22位作为输出数据的低 7位,舍弃其余数据位。图 7是对 20 MHz正弦信号sinc插值降采样后的仿真结果,其综合工具为 ISE9.2,目标器件为 Xilinx公司 Virtex-5系列的 XC5VSX50tff1136-1,仿真平台为 Modelsim SE 6.5。

图 7 20MHz正弦信号sinc插值后的仿真结果

仿真结果表明,插值降采样后的信号仍是比较完美的正弦信号。

3 实验与结果

本节对所设计的模块在板卡上进行了实验。其中,ADC的采样信号是频率为 20 MHz的正弦信号,采样时钟频率为 600 MHz;它们均由 Agilent 4 000 MHz脉冲发生器产生;采样长度为 8比特,采样点数为 16 384[7-8],ADC输出到 FPGA芯片的数据速率为 300 MHz.试验调试方案如图8所示。

启动 FPGA,让各模块正常工作,并用 Xilinx公司的 ChipScope Pro Analyzer软件对从 RAM缓存 2输出的数据进行分析,实验结果如图 9所示。

图 9表明,高速数据经过文中所设计的模块处理后,其输出仍然为比较完美的正弦信号。

图 8 实验调试方案

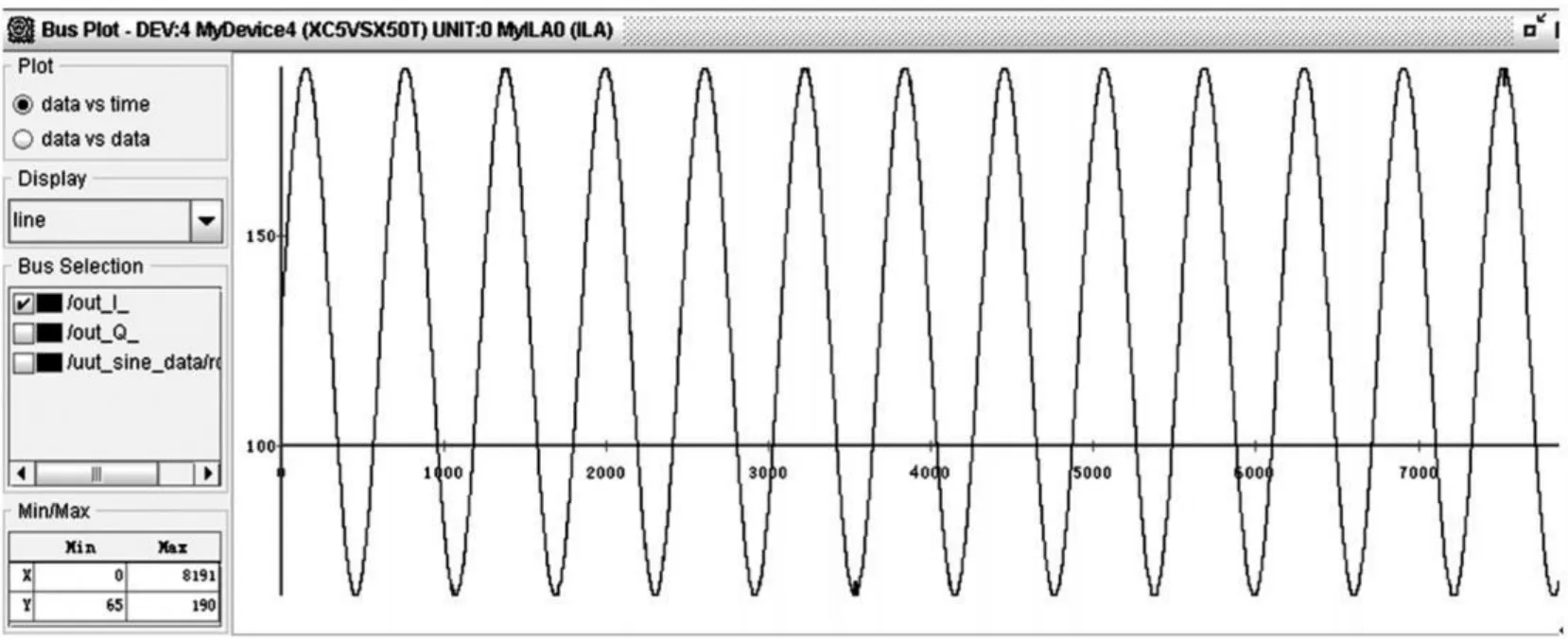
图 9 实验结果

4 结论

长时间的测试表明,当 ADC的采样信号频率在

20 MHz至 500 MHz变化时,系统均可以稳定可靠的工作,这就表明了文中所设计方案的可靠性与优越性,为合成孔径雷达系统距离向数据预处理模块设计提供了一种可行的方案。同时,在不严重影响成像质量的前提下,本设计方案还可以应用于方位向数据的处理中。

[1] Yeo T S,Zhang CB,Lu Y H,et al.Development of a SARDigital System[J].IEEE AESMagazine,1999,14(5)：37-41.

[2] 郭智,丁赤飚,吴一戎,等.一种高分辨率机载 SAR实时数据处理系统设计[J].电子与信息学报,2004,26(7)：1120-1125.

[3] 禹卫东,吴淑梅.距离-多普勒方法中的几种插值算法比较[J].电子与信息学报,2001,23(3).

[4] 洪文,胡东辉译.合成孔径雷达成像 -算法与实现[M].北京：电子工业出版社,2007：36-38.

[5] 金剑,唐宁等.∑-△DAC中多级插值滤波器的研究与设计[J].电子器件,2009,32(5).

[6] 王宇,张志敏,邓云凯,等.SAR实时方位预处理中的量化误差分析[J].现代雷达,2006,28(2).

[7] 袁孝康.星载合成孔径雷达导论[M].北京：国防工业出版社,2003：322-325.

[8]Sathaye S,Ramakrishnan K,Yang H,et al.FIFO Design for a High-Speed Network Interface[C]//IEEE Local Computer Networks Conference,1994：2-11.

[9] 夏宇文.Verilog数字系统设计教程(第 2版)[M].北京：北京航空航天大学出版社,2008：105-109.