考虑高层建筑的高分辨率卫星影像几何定位
乔 刚 ,王卫安
(1.同济大学 测量与国土信息工程系, 上海200092;2.同济大学 空间信息科学及可持续发展应用中心, 上海200092;3.同济大学现代工程测量国家测绘局重点实验室, 上海200092)
IKONOS (伊科诺斯), QuickBird (快鸟),WordView-1 等高分辨率卫星影像带来了卫星摄影测量的新时代, 使得某些以前只能通过航空遥感方式完成的大比例尺制图可以由卫星遥感完成[1],在测绘制图、城市规划、交通、水利、农业、林业、环境资源遥感与管理等民用领域有着较广阔的应用[2-5] .高分辨率卫星影像的各种应用中首先要解决的是高精度的几何定位[6-8].高分辨率卫星影像的几何定位模型主要包括严格传感器模型和通用定位模型等, 其中通用定位模型中的有理函数模型(rational function model,RFM)由于定位精度高、计算简单、可以实现卫星传感器参数隐藏等优点而被广泛使用.现在已有大量的文献对RFM的适用性和各种性质进行了研究[9-11].
国内外已有的高分辨率卫星影像几何定位研究成果大都是针对地形平坦地区或丘陵地区.这些区域存在地物简单、高程变化连续和控制点(ground control points ,GCPs)信息获取相对容易等特点, 因而已经有比较统一的定位模型与结论[12-13].文献[14-16] 对上海地区的高分辨率定位精度提高模型以及广义定位模型进行了研究, 但是这些研究也主要是针对城市地形平坦地区, 对考虑城市高层建筑的高分辨率卫星影像几何定位研究尚不够深入.而城市高层建筑区域的高分辨率卫星影像几何定位存在特殊性:地面平坦、地物复杂、高层建筑物密集;在小区域范围内高程不连续, 存在高程差突变;地面控制点获取相对容易, 而建筑物上控制信息获取存在困难.因此,本文拟在前期研究的基础上, 进一步提出考虑城市高层建筑的高分辨率卫星影像几何定位精度提高方法, 探讨在控制点位于平坦地面时对高层建筑进行高精度的几何定位.
1 模型描述
1.1 传统物方几何校正模型
高分辨率卫星影像(如IKONOS)一般提供用于RFM计算的有理多项式系数(rational polynomial coefficients,RPCs),表示从3 维空间坐标(标准化的WGS84 纬度、经度和大地高)到2 维影像坐标(标准化的影像行列坐标)的直接变换[17-18]:
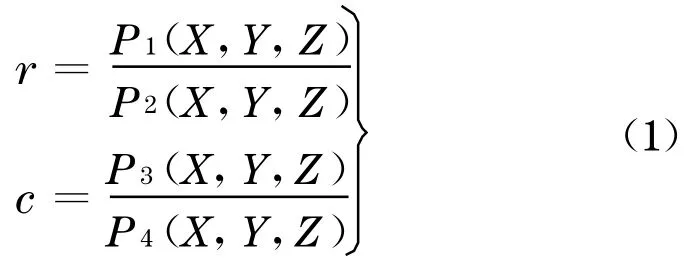
式中:r和c分别为影像的行和列坐标,Pi(i=1,2 ,3,4)为物方坐标X,Y,Z的3 阶多项式函数, 其表达式为
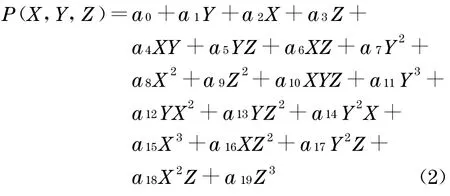
式中ai(i=0,1,…,19)为RPCs .RFM可以通过最小二乘平差迭代求解, 进行3 维重建, 获得物方坐标X,Y,Z.
这些RPCs 通过严格传感器模型计算得来.由于卫星传感器参数本身受到定轨定姿误差、大气折射误差等各种因素的影响, 使得通过这些参数计算得到的定位坐标存在系统误差.这种系统误差可以通过加入控制点的方式在物方或像方空间进行减弱或消除[19].本文主要研究物方几何定位模型及其改进模型.
物方几何校正模型是在通过RPCs 求解出影像点的3 维坐标以后, 建立控制点坐标与求得的3 维坐标之间的转换模型, 求出转换参数以后再对影像点求得的3 维坐标进行几何校正.建立这2 个WGS84 坐标系之间的坐标转换关系, 可以使用平移模型、平移缩放模型、仿射模型和二阶多项式模型等[20] .各种模型需要的最少控制点个数:平移模型需要1 个控制点;平移缩放模型需要2 个控制点, 仿射模型需要4 个控制点,二阶多项式模型需要10 个控制点[18,20].
1.2 改进的物方几何定位模型
由于物方几何校正的过程在数学上表示是2 个3 维坐标系之间的转换问题,转换参数的解答是通过对应的控制点拟合平差来实现的.当模型建立以后,模型的应用转变为3 个方向对应坐标的内插或者外推问题.一般情况下, 在数值计算中,当知道数学模型以后, 内插是不会出现问题的, 但是外推就不一定.当研究区域在平坦区域与丘陵地区时,控制点获取相对容易, 高程上可以覆盖整个研究区域,高程上属于内插.在城市建筑物密集区域,高层建筑物控制点获取存在困难, 这样大部分控制点只能从地面获取.当控制点全部位于地面时, 由于高程差非常小,只有1~3 m,这样建立起来的转换模型只能有效对高程差在此1~3 m 之内的点进行有效的坐标变换[15] ;而对于高程差超出此范围的点, 则变为一个外推问题.在这种情况下,外推的结果是将偏差成倍地放大, 计算结果是不正确的.在城市建筑物密集区域, 建筑物高度为数十米甚至数百米, 高程差早已经远远超出了地面控制点所能控制的范围, 所以外推的结果是完全错误的.
针对这种情况,本文提出物方几何校正模型的改进模型,将物方模型中平面变换式中的Z项去除, 同时将高程变换式中Z的缩放项及二次项去除.由于平移模型不存在高程方向外推, 则不进行改进,平移缩放模型改进以后高程方向的表达式与平移模型相同,可以得到与平移模型相同的结果.以仿射模型和二阶多项式模型为例,可以得到改进的物方几何模型
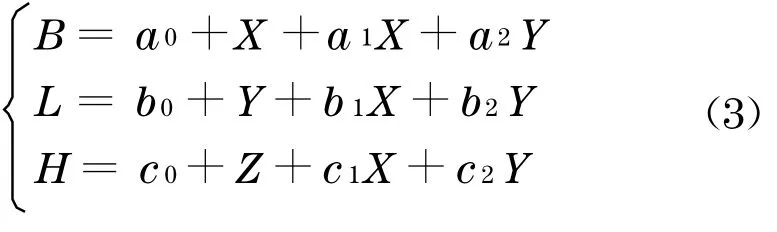
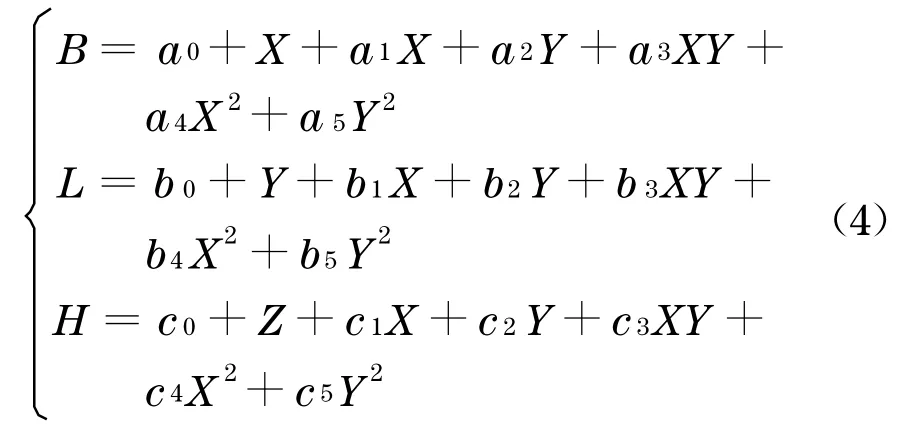
式中:(B,L,H)为地面控制点坐标;(X,Y,Z)为与地面控制点坐标对应的通过RFM计算得到的坐标;(a0,a1,…,b0,b1,…,c0,c1,…)为转换系数.这种改进的物方几何校正模型由于移除了Z项对于平面和高程各个方向的旋转缩放及更高项的影响, 理论上可以避免由于Z方向外推造成的计算错误.
2 研究区域与数据
本文的实验区域位于上海市中心城区(图1), 区域内地面平坦,只有1~3 m 的高程起伏.位于北纬31°08′52 .8″~31°17′59 .6″, 东经121°25′28 .9″~121°36′49 .0″,高程范围12~15 m, 面积为300 km2.研究区域内地物复杂, 建筑物密集,建筑物高度从数10 m 到400 m 不等.
图1 研究区域示意图Fig .1 Study area
两景QuickBird Basic 影像分别采集于2004 年2 月和5 月,覆盖范围与上述研究区域重叠, 构成一对异轨立体影像.两景影像扫描方式均是向前扫描,影像的元数据中包含卫星高度角和方位角, 根据文献[7] 中公式计算得到影像交会角为25 .9°, 表明这两景影像适合构成立体像对来进行地物3 维计算和量测.DigitalGlobe 公司提供全色和多光谱影像, 分辨率分别为0 .7 m 和2 .8 m .本文采用其中的两景全色影像,像素分辨率分别为0 .682 m 和0 .717 m .从DigitalGlobe 公司获取的Basic 卫星影像是原始数据,没有经过任何几何校正,所以同地形图比较存在很大的变形,进行GPS 选点有很大的困难.本文首先对原始影像进行初始几何校正, 采用遥感影像软件ERDAS .经过初始校正后的卫星影像如图2 所示.

图2 异轨立体Qu ickBird 卫星影像Fig .2 Profile of Quick Bird across-track stereo imagery
实验所需的控制点采用基于上海市V RS 系统的GPS 外业测量获得[21].考虑到上海中心城区地面平坦与高层建筑物密集的特点, 本文考虑2 种类型的GPS 测量点, 地面GPS 测量点和建筑物楼顶GPS 测量点.地面点包括如道路交叉点、混凝土角点以及矩形物体角点.本文实验中使用地面GPS 测量点66 个,建筑物楼顶GPS 测量点采集到16 个.地面点的高程为12~15 m,建筑物楼顶点高程为30~360 m .G PS 测量点的精度为平面方向0 .02 m ,高程方向0 .05 m .GPS 测量点分布如图3 所示,图中外边框为2004 年2 月QuickBird 影像范围.
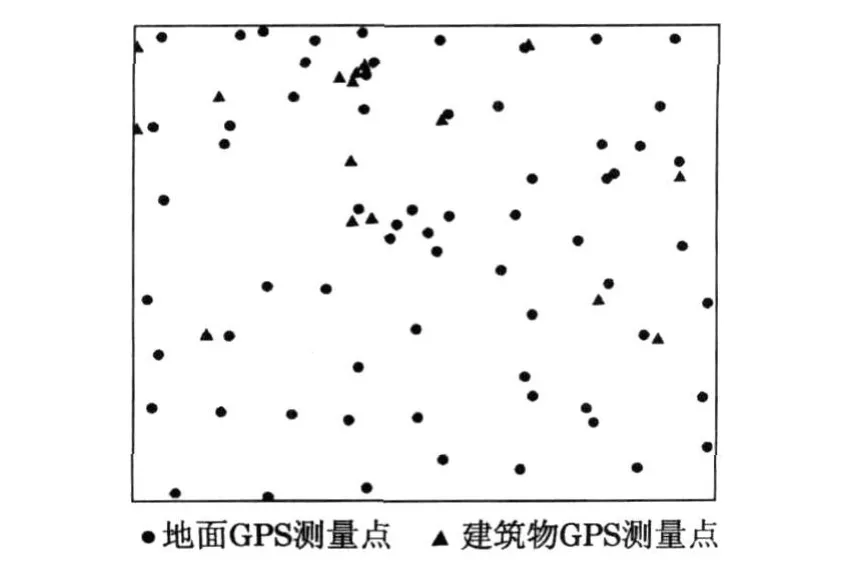
图3 GPS 测量点分布图Fig .3 Distribution of GPS survey points
3 实验结果与分析
3.1 控制点与检核点都位于地面的传统物方几何校正
研究控制点和检核点都位于地面时研究区域内传统物方几何定位模型精度, 分析控制点平面分布均匀时不同数目对传统物方不同几何校正模型的定位结果.控制点分布如图4 所示, 为了方便, 只给出控制点,检核点为66 个GPS 地面测量点除掉控制点以后剩下的点.
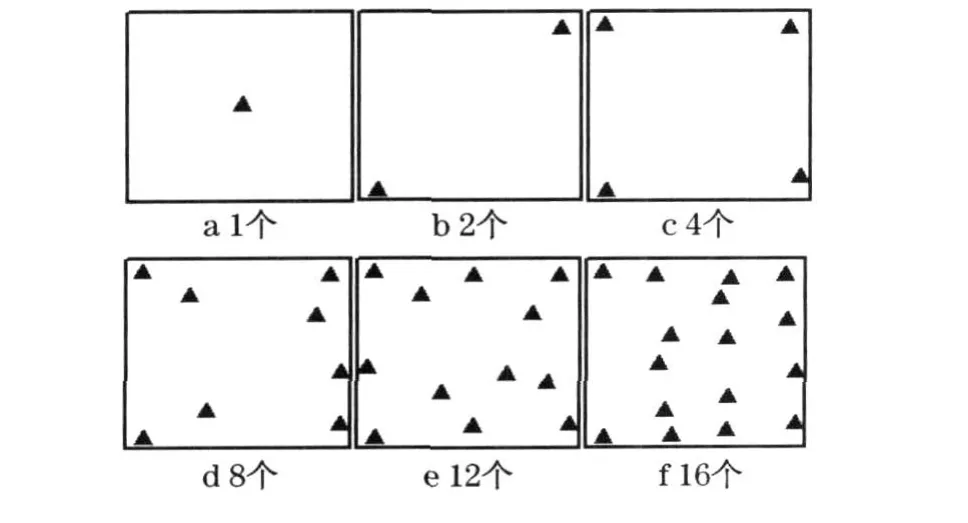
图4 控制点个数与分布Fig.4 GCP number and distribution
控制点平面分布均匀, 包含数目为1 ,2,4 ,8,12 ,16 等6 种情况,其高程变化不大,几乎位于同一水平面上,高差在3 m 之内.为了方便起见, 本文对纬度、经度、高程3 个方向的定位精度进行分析.
本节采用传统物方几何校正中的4 种模型进行了研究,包括平移模型、平移缩放模型、仿射模型和二阶多项式模型.图5 是精度分析图, 其中RMSE_B表示纬度方向的RMSE,RMSE_ L 表示经度方向的RMSE ,RMSE_H 表示高程方向的RMS E .
由图3可知,焦亚硫酸钠对抑制大豆制品褐变效果显著。总体趋势为:随着焦亚硫酸钠含量的增加,抑制褐变效果越加明显,但在其添加量为0.03%时,评分略微有所下降。这是因为焦亚硫酸钠能抑制葡萄糖等还原糖生成5-羟基糠醛,从而阻止美拉德反应的发生[9]。故综合考虑国家食品添加剂添加标准及抑制褐变效果,添加量在0.02%最合适[10]。
从图5 中可以看出, 当在大城市地面平坦区域进行高分辨率卫星影像几何校正时,如果控制点和检核点都位于平坦地面上, 对于传统物方成像模型,平移模型可以有效地消除RFM几何定位中存在的系统误差,达到平面2 .5 m 左右、高程3 m 左右的几何定位精度;存在均匀分布的多余控制点的条件下,平移缩放模型可以得到比平移模型更好的几何定位效果;仿射模型具有最优的几何定位表现,可以得到平面0 .65 m 、高程0 .5 m 左右的几何定位精度;而二阶多项式模型由于考虑了过多的非线性因素对几何形变的影响,造成了定位结果的不稳定,可能会产生求解结果的震荡,因而在这种情况下不推荐使用.
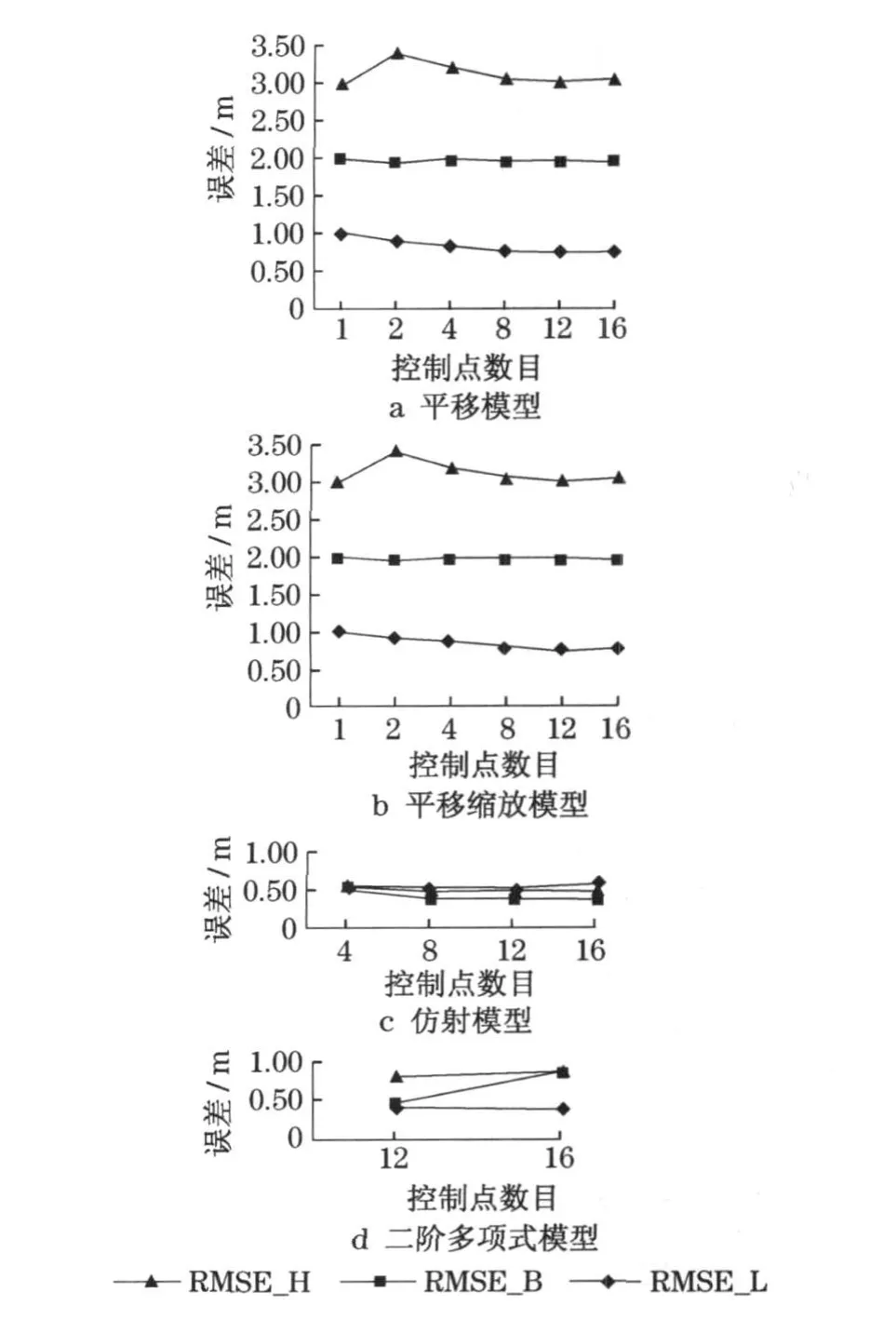
图5 传统物方成像模型几何校正结果Fig .5 Geometric correc tion resu lts of traditional imaging model
3.2 控制点位于地面、检核点位于地面和建筑物楼
顶的传统物方几何校正
当控制点位于地面、检核点分布于地面和建筑物楼顶时的实验控制点分布仍如图4 所示.此时的实验结果中, 传统物方几何校正模型中除了平移模型以外, 另外几种模型都不能正确地进行高分辨率卫星影像几何校正,误差有上百米甚至是上千米.通过查看每个检核点的校正结果可以发现, 计算结果的正确与否与检核点的高程相关.当检核点位于地面时, 检核点高程与控制点高程几乎相同, 差值在1~3 m ,这时在3 个方向上计算得出的几何校正结果与检核点的值非常接近;检核点高程与控制点高程差异越大, 则在3 个方向上计算得出的几何校正结果与检核点的差异值也越大.
表1 是研究区域控制点全部位于地面时的部分检核点的3 个方向的差异值, 校正模型为传统物方二阶多项式模型, 控制点个数为16 .从表中可以看出,当16 个控制点全部位于地面时, 控制点的高程范围为12~14 m ,检核点17 高程为14 .10 m ,位于地面, 其3 个方向的几何校正结果与测量值的差值都非常小,在1 m 之内.检核点1,14,16 都位于建筑物楼顶, 并且其高程值逐渐增大, 可以看出点1 的3 个方向几何校正结果与测量值差异在数10米;点14 的差异值已经达到1 000~2 000 m ;而点16 则达到了3 000~7 000 m .实验结果说明当控制点全部位于地面时,传统物方几何校正模型可以有效提高地面点的定位精度, 但是对于建筑物楼顶点,几何校正结果会随着高程的增大而逐渐变差,出现计算错误.
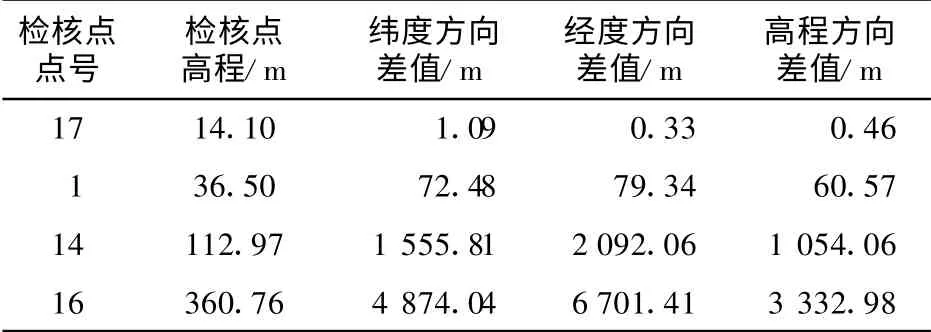
表1 控制点位于地面时部分检核点几何校正结果差异(控制点高程范围12~14 m)Tab.1 Selected coordinates discrepancy of ICPs when GCPs are on the groun d(GCPs elevation range:12~14 m)
3.3 改进物方几何校正模型实验结果
3.3.1 控制点和检核点都位于地面的实验分析
采用改进的物方几何校正模型对控制点和检核点都位于地面时进行了几何校正计算, 表明这种改进的校正模型具有很高的几何定位稳定性, 可以大大提高几何定位校正的精度.图6 列出了改进的物方校正模型二阶多项式变换的结果.
改进的二阶多项式模型的控制点分布如图4e,f所示.从图6 中可以发现,当控制点数目为12 时, 纬度方向几何定位精度为0 .38 m ,经度方向的几何定位精度为0 .40 m,高程方向为0 .51 m ;当控制点数目为16 时, 3 个方向的几何定位精度分别为0 .37 ,0 .38和0 .47 m .实验结果表明, 这种改进的几何校正模型由于消除了高差外推的影响, 应用于平坦地区时可以克服传统模型高阶震荡的缺点, 达到更为稳定的几何定位结果.
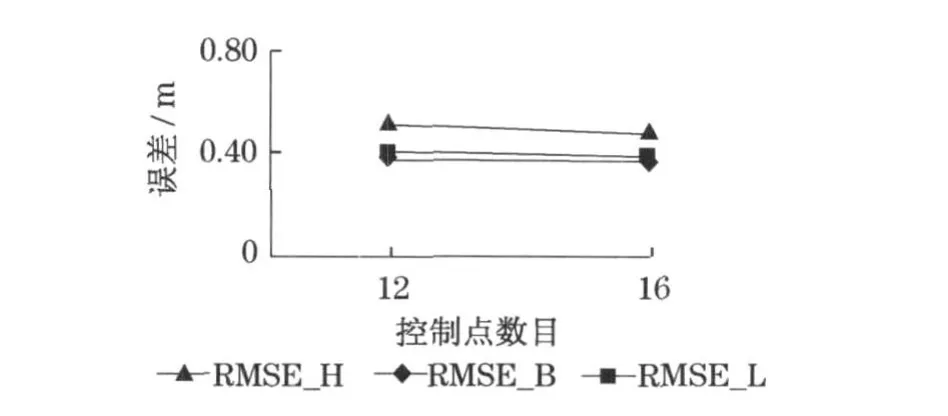
图6 控制点和检核点都位于平坦地面时改进物方二阶多项式模型精度分析Fig.6 Geo-positioning accuracy of the modified secondorder polynomial model when GCPs and ICPs are both on f lat ground
3.3 .2 控制点位于地面、检核点位于地面和建筑物楼顶的实验分析
控制点位于地面、检核点位于建筑物楼顶时, 采用本文提出的改进物方成像几何校正模型的实验控制点分布,如图4c, d ,e ,f 所示.改进的仿射模型和二阶多项式模型计算结果的精度分析如图7 所示.
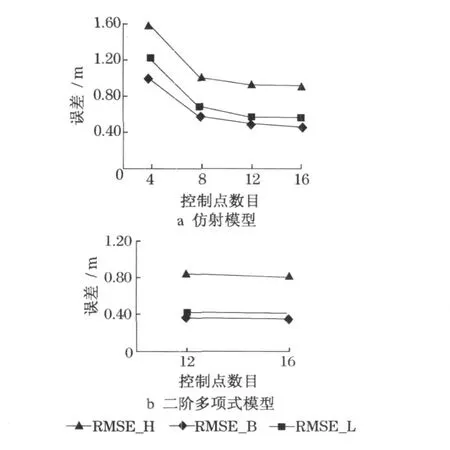
图7 改进的几何校正模型结果分析Fig .7 Accuracy analysis of the modified geometric correction model
从图7 可以看出, 这种改进的物方几何校正模型可以有效地避免由于控制点高程相近而造成的外推问题,消除RFM中存在的固有系统误差,得到高精度的几何定位结果.改进的仿射模型控制点为4时纬度方向几何定位精度为1 .00 m,经度方向为1 .23 m ,高程方向为1 .59 m ;随着控制点个数的增加,3 个方向的定位精度都有所提高,到控制点个数为16 时,纬度方向为0 .46 m,经度方向为0 .55 m ,高程方向为0 .91 m .改进的二阶多项式模型当控制点为16 时的几何定位精度纬度方向在0 .36 m ,经度方向为0 .42 m ,高程方向为0 .81 m .
4 结论
(1)传统物方几何校正模型可对地形平坦地区有效地进行高分辨率卫星立体影像几何校正, 消除存在的系统误差影响.仿射模型具有最佳的几何定位精度,可以得到平面0 .65 m ,高程0 .5 m 精度;二阶多项式模型会产生求解结果的震荡.
(2)对于城市高层建筑, 控制点位于地面时传统物方几何校正模型中除了平移模型以外, 都不能对高层建筑物进行高分辨率卫星影像几何校正.计算结果的正确与否与检核点的高程相关, 检核点位于地面时, 几何定位精度非常高;位于建筑物楼顶时,随着建筑物高程增加, 由于高程外推影响, 几何定位精度越来越差,出现计算错误.
(3)本文提出的改进物方几何校正模型可以有效地对城市高层建筑区域, 控制点位于地面时的高层建筑物进行高分辨率卫星影像几何校正.建议控制点水平分布均匀, 并且个数达到10 个左右, 这时可以达到0 .6 m 以内的平面精度和0 .8 m 左右的高程精度.这种改进的物方模型可以有效地避免由于高程变化而造成的外推问题, 具有非常稳定的几何定位能力.
[1] Li R.Potential of high-resolu tion satellite imagery for national mapping products [J] .Photogrammetric Engineering &Remote Sensing,1998, 64(12):1165.
[2] Di K,Ma R, Li R.Geometric processing of IKONOS geo stereo imagery for coastal mapping applications[J] .Photog rammetric Engineering & Remote Sensing,2003, 69(8):873.
[3] 张永生, 巩丹超, 刘军, 等.高分辨率遥感卫星应用——成像模型、处理算法及应用技术[M] .北京:科学出版社, 2004.ZH ANG Yongsheng,GONG Danchao,LIU Jun, et al.The application of high resolution satellite of remote sensingimaging model, processing algorithmand applied technique[M] .Beijing :Pub lishing H ouse of Science,2004.
[4] Habib A, Shin S W,K im K,et al .Comprehensive analysis of sensor modeling alternatives for high-resolution imaging satellites [J] .Photogrammetic Engineering & Remote Sensing,2007, 73(11):1241.
[5] Toutin T .DTMgeneration from IKONOS in-track stereo images using a 3D physical model [J] .Photogrammetric Engineering & Remote Sensing,2004, 70(6):695.
[6] Zhou G,Li R.Accuracy evaluation of ground points from IKONOS high-resolution satellite imagery[J] .Photogrammetric Engineering &Remote Sensing,2000, 66(9):1103.
[7] Li R, Zhou F,Niu X,et al.In tegration of IKONOS and Quick Bird imagery for geopositioning accu racy analysis[J] .Photog rammetric Engineering & Remote Sensing,2007, 73(9):1067.
[8] Tao C V,H u Y,Jiang W.Photogram metric exploration of IKONOS imagery for map ping applications[J] .International Journal of Remote Sensing,2004, 25(14):2833.
[9] Di K,Ma R, Li R.Rational functions and potential for rigorous sensor model recovery [J] .Photogrammetric Engineering &Remote Sensing,2003, 69(1):33.
[10] Hu Y, Tao C V .Updating solutions of the rational function model using additional control information [J] . Photogrammetric Engineering & Remote Sensing ,2002,68(7):715.
[11] Tao C V,H u Y .Acomprehensive study of the rational function model for photogram metric processing [J] .Photog rammetric Engineering & Remote Sensing,2001, 67(12):1347.
[12] 陈楚江,李德仁, 朱庆.IKONOS-2 在西藏的空间定位及其精度研究[J] .武汉大学学报:信息科学版, 2005, 30(9):782.CH EN Chujiang,LI Deren, ZHU Qing .Research of Ikonos-2 positioning and accu racy in Tibet of China[J] .Geomatics and Information Science of W uhan University,2005, 30(9):782.
[13] Aguilar MA,Aguilar F J, Aguera F ,et al.Geometric accuracy assessment of QuickBird basic imagery using different operational approaches[J] .Photogram metric Engineering &Remote Sensing,2007, 73(12):1321.
[14] 刘春, 展昀, 吴杭彬.辅助控制点下快鸟影像定位求解及其精度分析[J] .同济大学学报:自然科学版, 2009, 37(7):983.LIU Chun,ZH AN Yun, WU Hangbin.Solution of geopositioning and its accu racy analysis in QuickBird imagery based on auxiliary ground control points[J] .Journal of Tongji University :Natu ral Science,2009, 37(7):983.
[15] 童小华, 刘世杰,叶勤.基于有理函数模型的QuickBird 立体定位精度分析[J] .同济大学学报:自然科学版, 2009, 37(4):555.TONG Xiaohua,LI U Shijie,YE Qin.Accuracy analysis and improvement of Quick Bird stereo positioning based on rational function model[J] .Jou rnal of Tongji University :National Science,2009, 37(4):555.
[16] 刘世杰,童小华.快鸟影像广义成像模型适用性分析[J] .同济大学学报:自然科学版, 2009, 37(7):974.LIU Shijie,TONG Xiaohua .App licability analysis of generalized sensor models for QuickBird imagery[J] .Journal of T ongji University :National Science, 2009, 37(7):974.
[17] Niu X, Di K,Wang J,et al .Geometric modeling and photogram metric processing of high-resolu tion satellite imagery [C] ∥Proceedings of the XXI C ongress of the International Society for Photogrammetry and Remote Sensing(ISPRS 2004, Commission IV,WG IV/7 ).Istanbul:Comm ittee of the XXI International Cong ress for Photog rammetry and Remote Sensing,2004:1-6.
[18] Qiao G,Wang W, Zhang J .3D geo-positioning based on biascompensated rational function model for Quick Bird imagery[C] ∥Proceedings of SPIE,Geoinformatics 2007.Nanjing :SPIE,2007:1-12.
[19] DigitalG lobe Inc.QuickBird Imagery Products-Produ ct Guide,Revision 5.0.URL[E B/ OL] .[2009-03-20] .h ttp:∥www.digitalglobe.com/ file .php/ 646/ QuickBird_ Imagery_ Produ cts-Produ ct_Guide .pdf,March 31.
[20] Wang J, Di K,Li R.Evaluation and improvement of geopositioning accu racy of IKONOS stereo imagery[J] .ASCE Journal of Su rveying Engineering,2005, 13(2):35.
[21] 季善标.上海市V RS GPS 台站网系统应用与管理[J] .城市勘测, 2007, 5:12.JI Shanbiao .Application and management of the Shanghai VRS GPS network system [J] . U rban Geotechnical Investigation & Surveying,2007, 5:12.

