国际组合套利机理及优化策略分析

陈伟忠,詹 欣

(同济大学经济与管理学院, 上海200092)

防范热钱流入以及可能随之而来的恶意套利行为是我国维持金融经济安全的重要策略.然而一般所能迅速、直接观察到的套利行为仅仅局限于同质资产之间,以及相关程度较高的资产之间.而对于套利对象多元化和套利路径复杂化的国际组合套利行为而言, 还很难迅速对其识别, 并快速做出最优的应对策略.随着我国金融业尤其是资本市场进一步地对外开放,加上改革和发展的不平衡, 我国很可能会不自觉地创造了国际组合套利机会, 并因此遭受到国际套利资本的攻击, 进而对国内经济和政策稳定造成冲击! 所以, 无论从理论研究还是从实际需求角度, 都需要对国际组合套利行为的机理进行深入探究,进而为我国防范和应对国际恶意套利行为, 维持稳定的金融环境提供方法和策略.

对国际组合套利的研究最初起源于为规避汇率风险而进行的套期保值研究, 如Odier 和Solnik 等研究了组合套期保值的问题[1-3].Fang 等研究了组合套利或套保的相关模型[4-9].而其余大量针对国际套利的研究基本可以归类于单一资产间的套利行为, 如利率套利、汇率套利和大宗商品套利等.

综上所述,当前仍然缺乏针对国际组合套利行为的系统性描述, 以及对其背后作用机理的剖析.本文在前人研究的基础之上, 以国际组合套利行为作为研究对象, 通过对国际套利定价理论的拓展, 构建影响资产价格的国际多因素模型;通过进一步的数理分析, 深入探究国际组合套利行为的内在机理;进而分析国际组合套利的风险及优化策略问题.

1 对国际组合套利行为的机理阐述

以Bruno Solnik[10]的国际套利定价理论为基础, 假设影响一国市场上风险资产的收益有m个国际公共宏观风险因素f1,f2,…,fm,n个国内宏观风险因素f′1 ,f′2,…,f′n,m+n=k,k远小于市场上资产的总数目.由此可以得到影响一国风险资产收益的国际宏观因素模型为

式中:R i,j为用另一国的货币j来测度的本国资产i的收益;E i,j为用另一国的货币j来测度该风险资产的预期收益;βim,j和β′in,j分别表示风险资产对国际和国内公共风险因素的敏感度;μi是残差项.其矩阵形式为

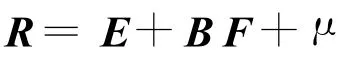
式中:B =[Bm|B′n],Bm,Bn分别为资产对国际和国内公共风险因素敏感度系数矩阵

如果不考虑外部环境因素, 正是由于单一市场和产业特有因素的存在,以及市场开放程度的影响,使得不同国家或市场的单一资产间相关性降低, 进而使单一资产间套利面临极大的风险.而国际组合套利的思想就是在原有资产的基础之上增加相关资产来构建组合, 尽可能地对冲掉降低资产相关性的因素,或者增加能提高资产相关性的因素,进而使新组合和另一资产之间或组合和组合之间形成强相关,实现配对;一旦配对的组合和资产之间, 或组合和组合之间由于价格波动形成了大的价差, 打破了其特有的无套利条件, 就有可能创造新的套利机会.

假设在国际范围内所有市场中包含N(N足够大)种资产, 不同市场的资产之间相关性不够强, 而不足以发生单一资产间的国际套利(或单一资产间套利风险巨大).可以选取其中的p种资产构建组合X,假设可能影响到这p种资产的全部因素有m种,根据式(1),其一般因素模型可以表示为

由于某一种资产不一定具有其他资产所具备的特有因素, 所以允许其中的部分β 值为0 .当选取某一组合权重:ωP=(ω1,ω2,…, ωp)T时, 组合X的收益可以表示为

同理,可以选取市场中的另外q种资产构建组合Y,假设可能影响到这q种资产的全部因素有n种,同时允许一般因素模型式中部分β 值为0 .那么,当选取某一组合权重:ωQ=(ω′1,ω′2,…, ω′q)T时,组合Y的收益可以表示为

根据上文的理论分析, 组合套利机会的构建就在于:选择恰当的ωP和ωQ,使得式(3)和式(4)中部分因素的加权系数为0 ;从而剔除了可能降低组合间相关性的因素,使得决定2 个组合X,Y收益的剩余因素大致相同.使2 个式子尽可能地逼近, 以提高2个组合的相关性, 进而实现组合配对.一旦由于价格波动使2 个组合的价差发生大幅偏离时, 就会形成国际组合套利机会.

2 对国际组合套利机理的数理分析

综上所述,国际组合套利的核心思想就是:用相关性相对较强的组合来替代原本难以配对的单一资产, 作为国际套利的主要对象, 以此拓宽国际套利的范围.假设只考虑国际市场上2 个组合X和Y之间的套利, 根据式(3)和式(4)得出2 个组合收益的矩阵形式如下:

从而有以下的命题及推论:

命题1 国际套利行为的分类归纳如下:①当p=1 ,q=1 时, 为单一资产之间的国际套利;②当p＞1 ,q=1 或p=1 ,q＞1 时,为资产组合与单一资产之间的国际套利;③当p＞1 ,q＞1 时,为资产组合与组合间的国际套利.②, ③两种情况统称为国际组合套利.

命题2 组合X和组合Y能发生严格的国际组合套利的必要条件是:rang B=rang B′.

证明 如果组合间能发生严格意义上的国际套利, 那么经线性变换后,影响2 个组合收益的剩余因素数目一定相同.也即:假设剩余因素数为k个, 且k＜m,k＜n,因素载荷矩阵B 和B′经线性变换后一定可以转化为下面的形式:

其中, Σ和Σ′为对角线上元素非0 的对角阵, 所以2个因素载荷矩阵的秩相同.

推论1 组合X和组合Y若能发生严格的国际组合套利, 那么必有影响全部组合收益的剩余因素数k小于等于2 个组合的公共因素数.

证明 用反证法.如果k大于组合的公共因素数,那么必然存在影响组合价格的特有因素.组合之间的相关性会降低,套利风险增大,严格的国际组合套利就不能发生.

命题3 在一段时间t至t+1 内,不考虑交易成本,假设β值稳定,由Δ=ωTPEX-ωTQEY决定国际组合套利机会的存在.

证明 当β 值稳定的时候, 不考虑残差项, 式(5)和式(6)的右边第二部分因素影响近似相等.只有当组合的期望收益存在差异时,才会在一段时间的始末出现组合间的价格差变动,出现套利机会.

进一步假设组合X和组合Y在t时刻的价格分别为P X,t和P Y,t,在t+1 时刻的价格分别为P X,t+1

和P Y,t+1,则t时刻的价差为S t=P X,t-P Y,t,t+1时刻的价差为S t+1=P X,t+1-P Y,t+1.由于 Δ =

ωTPEX-ωTQEY为两组合的期望收益差, 而且构建正、反向头寸的初始资金量相同, 那么当β 值稳定的时候,从t到t+1 时刻组合间的价格差变化S t+1-S t可以用期望收益差Δ来替代.当Δ＞0 时,表示t到t+1 时刻组合间的价格差变大(图1),即S t+1＞S t,对应的套利策略是:在t时期买入组合X卖出组合Y,在t+1 时期做相反的头寸平仓获利.而当Δ＜0时,表示t到t+1 时刻组合的价格差变小, 对应的套利策略是:在t时期买入组合Y卖出组合X,在t+1 时期做相反的头寸平仓获利.

3 国际组合套利风险及优化策略分析

很显然, 对于国际组合套利者来说, 其优化策略应该是选择合适的组合权重, 使给定期望收益的情况下风险水平最小, 或给定风险水平的情况下期望收益最大.

根据上文可以得到组合X和组合Y的价格差为:

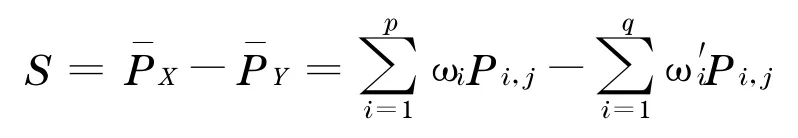
从而可以推导出两组合价格差的方差为

式中:XP为组合X中资产价格向量(P1,j,P2,j,…,P q,j)T的协方差矩阵;YQ为组合Y中资产价格向量(P1,j′,P2,j′, …,P q,j′)T的协方差矩阵.同时假定X PY Q均为正定矩阵.而

σpq为组合X 中的资产和组合Y 中的资产价格的协方差.

命题4 组合间存在最优套期保值策略的必要条件是组合X和组合Y的方差相等.

证明 单从组合间套期保值最优化的角度考虑, 当期望收益或价差水平锁定时,应选择组合向量ωp和ωQ使式(7)最小化.根据▽σ2s=0 整理可得

如存在ωp和ωQ使式(8)成立, 即组合X和组合Y的方差相等时, 则m in σ2s=0 ,存在最优套期保值策略.

推论3 当P=1 时,根据式(8)即可得到多种资产对单一资产的最优套期保值率向量为:ωQ=Y-1QCQ1.此推论与文献[6] 中结论一致.

进一步探讨组合间套利策略的情况,沿用文献[11] 等采用的均值-方差法.不考虑交易成本, 假设国际组合套利者的效用大小与其期望收益成正比,与价差波动成反比, 可得一种套利者的效用函数表达式如下:

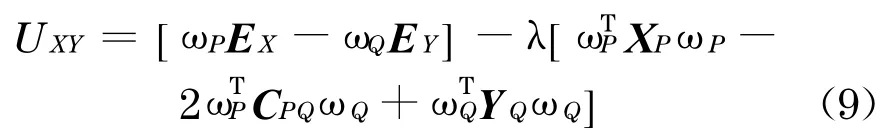
其中λ为效用风险系数.对于国际组合套利者来说,即选择合适的组合权重ωp和ωQ,使式(9)最大.式(9)分别对ωp和ωQ求一阶偏导数并整理得

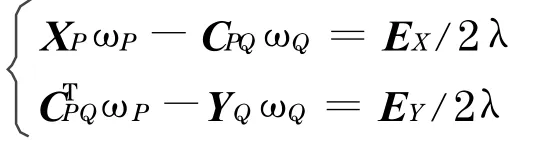
写成矩阵形式为

式(10)中负号表示反向头寸.由于上文假定XP和YQ均为正定矩阵,所以XP和YQ均存在逆矩阵.可解得

式中:D =YQ-CTPQXPCPQ;IP和IQ为单位阵.由式(10)和式(11)可以得到,不考虑交易成本且给定预期收益的情况下,国际组合套利优化的头寸比例向量为

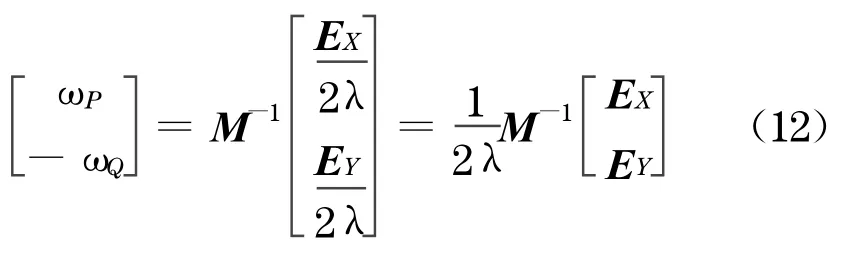
4 实证研究

4.1 使用数据说明

运用上文的结论,以2005 年7 月21 日汇率制度改革以来至2010 年5 月21 日中国和美国股票市场之间的一级行业指数作为研究对象, 分析组合套利优化策略, 使用的数据说明如下:①沪深300 指数和标普500 指数的每周收盘均价;②新华富时一级行业指数的每周收盘均价(包括新富电气、新富工业、新富公用、新富基材、新富金融、新富科技、新富石气、新富卫生、新富消服和新富消品十大行业指数);③标准普尔美国行业指数的每周收盘均价(包括 Consumer Discretionary,Consumer Staples ,Financials,Health Care,Information Technology ,Telecommunication Service, Utilities,Energy ,Industries ,Materials 十大行业指数).以上数据均由W ind 咨询公司提供.

对上述数据有如下说明:①如果选用日数据, 会由于中美节假日不同导致交易日不同, 使数据在时间上的连续性受到影响,出现大量断点;而如果选取月数据, 则会由于样本数目过少,而影响实证研究的效果;选取周数据基本可以避免前两者的缺陷, 除五一、国庆、春节等周缺失极少量数据外, 其余时间序列均连续,另外每一种指数都有244 个样本数据, 样本大小足够.②实际中的套利本应选取具体的金融产品, 如行业ETF(Exchange Traded Fund,交易所交易基金)基金或其他指数产品.但是虽然美国拥有行业E TF 产品, 如SPDRs(Standard & Poor' s Depositary Receipts)、HO LDRs(Holding Company Depositary Receip ts)等, 而中国目前没有行业E TF产品.所以为了便于进行类比, 以及仅从理论研究角度考虑, 本文直接使用基本的指数价格替代了具体的金融产品交易价格.

4.2 国际套利组合的构建和求解

假定套利者在构建头寸的初期锁定了汇率风险, 首先分别对两国市场的行业指数做相关性分析.剔除相关性＜0 .6 的低相关性序列, 保留相关性＞0 .6的序列,得到表1 .

表1 中美市场行业指数相关性分析结果Tab.1 Relativity analysis of industrial indices between China and America

从表1 中可以看出, 美国的能源行业对中国市场的4 个行业指数的相关性均大于0 .6 ,所以在构建国际套利组合时, 美国市场中选择能源行业指数, 而中国市场中如果仅选择与之最为相关的新富石气指数, 显然不能够满足资产间强相关的条件,因此选择新富工业等4 个指数构建组合.考虑到需要对冲掉一国市场特有的风险因素对行业指数的影响, 在资产组合中须分别增加沪深300 指数和标准普尔指数.各种资产的收益率均值如表2 所示.

表2 组合中资产的收益率均值Tab.2 Mean value of the assets' yield rate in the portfolios

运用第4 部分的方法, 可以计算出资产方差-协方差的逆矩阵M-1:

运用式(12), 求解出优化的组合套利头寸比例系数,并以能源行业的系数为基准, 得出相对的头寸比例系数如表3 所示.

表3 组合中资产的头寸比例系数表Tab.3 Position ratio of the assets in the portfolios

运用表3 中的权重构建2 个组合, 即ωP=(1 ,-0 .085 2)T,ωQ=(0 .016 6 ,-0 .065 3 ,-0 .128 3 ,-0 .038 0,0 .540 0)T.

美国资产组合为:Pa=能源-0 .085 2 ×标普500 ;

中国资产组合为:Pc=0 .016 6 ×新富公用-0 .065 3 ×新富工业-0 .128 3 ×新富基材-0 .038×新富石气+0 .54 ×沪深300 指数.计算两组合的相关系数为0 .71 ,相对于单一资产间的相关性得到了提升.

5 总结

本文从国际套利定价模型出发,构建了影响一国风险资产收益的国际多因素模型, 在此基础上探索了国际组合套利的机理, 即通过对冲掉一部分特有风险, 提升组合之间的相关性, 实现资产组合的有效配对, 从而拓展了套利对象的范围.通过进一步的数理分析,深入探究了国际组合套利的风险及优化策略.与单一资产相比, 资产组合的β 值较为稳定,而且资产组合的残差也比较低, 这就便于整个套利过程的操作, 降低了套利的风险.但是需要指出的是, 均值方差法所计算出的头寸比例只是一种优化策略, 但并非达到最优.从本文的实证研究可以看出, 均值-方差法不具备从多个资产中选择最佳资产构建套利组合的功能, 组合的相关系数为0 .71,仍未达到强相关性的要求, 使得套利存在一定的风险, 因此还需要进一步探究新的方法来解决这一问题.

[1] Odier P, Solinik B .Lessons for international asset allocation[J] .Financial Analysts Journal, 1993, 49(2):63.

[2] Celebuski M, Hill J, Kilgannon J.Managing currency exposure in international portfolios[J] .Financial Analysts Journal,1990, 46(1):16.

[3] Filatov V,Rappaport p.Is complete hedging optimal for international bond portfolios[J] .Financial Analysis Journal,1992, 48(4):37.

[4] FANG Shuhong .Amean-variance analysis of arbitrage portfolios[J] .Physica A,2007, 375(2):625.

[5] Clare A D,Oozeer MC .Hedging sterling eurobond portfolios:a proposal for eurobond futures contract[J] .Applied Financial Economics, 2001, 11(1):37.

[6] 马永开,唐小我.组合套期保值策略及其理论研究[J] .预测,1999(4):48.MA Yongkai,T ANG Xiaowo .Research on the strategy and theory of portfolio hedging[J] .Forecasting,1999(4):48.

[7] 刘燕武,张忠桢.组合套期保值的多元线性回归特征[J] .系统管理学报, 2008(3):303.LIU Yanwu, ZHANG Zhongzhen.Study on characteristics of multiple linear regressions for cross hedging [J] .Jou rnal of System s and Management,2008(3):303.

[8] Carassus L,Huyen P,Nizar T .No Arbitrage in discrete time under portfolio constraints[J] .Mathematical Finance, 2001, 11(3):315.

[9] Bank P,Baum D .H edging and portfolio optimization in financial markets with a large trade[J] .Mathematical Finance,2004, 14(1):1.

[10] Solnik B H .International arbitrage pricing theory[J] .Journal of Finance, 1983, 38(2):449.

[11] 唐衍伟,陈刚.静态最优期货价差套利头寸比例估计[J] .系统工程, 2008(1):51.TANG Yanwei, C HEN Gang .Estimating of the positions ratio of static optimal futures spread[J] .Systems Engineering,2008(1):51.