莱芜煤田东港井田19#煤层断裂构造分形特征分析＊

魏久传 赵 蕾 尹会永 孔维鲁

(1.山东科技大学地质科学与工程学院,山东省青岛市,266510;2.山东省郓城煤矿,山东省郓城县,274718)

近年来,国内外许多学者研究了断裂构造的分形结构特征及其在矿床、油气田、地震等方面的应用,取得了许多有意义的成果。分形理论为断裂构造的定量研究提供了一种全新的方法。本文采用盒维法和信息维法对东港井田19#煤层的断裂构造特征进行分析,在对已采区构造定量研究的基础上,对未采区构造进行了预测。

1 东港井田地质概况

莱芜煤田位于鲁中隆起泰莱凹陷中,为一轴向NE的倾伏向斜,南北分别以新甫山凸起和鲁山凸起与新汶煤田及淄博煤田毗邻。东港井田总体为一单斜构造形态,位于西港井田东北部、潘西井田西南部,地层走向NW。断裂构造发育,落差大于30 m的断层13条,见图1。

井田地层由老至新发育有太古界、古生界寒武系、奥陶系、石炭系、二叠系、中生界侏罗系、新生界古近系以及第四系,地表仅出露侏罗系。含煤地层为华北石炭二叠系,主要含煤地层为山西组和太原组,其中可采煤层有5层(2#、4#、7#、15#、19#煤层),目前主采19#煤层,19#煤层为稳定可采煤层,煤厚1.06～3.42 m,平均2.49 m,煤层结构较简单,可采性好。

2 东港井田19#煤层断裂构造分形维数计算

2.1 盒维法

盒维法是最常用的分形分析方法。该方法以不同边长为r的正方形格子构成网格平面去覆盖断层平面分布图,统计出包含断层的网格数N(r)。

根据分维的定义:N(r)=Cr-D0,将N(r)和r分别取对数后推导得:

将计算所得的一系列[lnr,lnN(r)]值进行线性回归分析,经验证lnr与lnN(r)的关系可以用分维定义的推导式来表征,为了判断这种线性关系关联的好坏,可借助相关系数,相关系数越趋近于1表明关联性越好。该直线的斜率就是所求的盒维数D0。D0的数值大小代表了断裂构造的复杂程度,数值越大表明断裂构造越复杂。

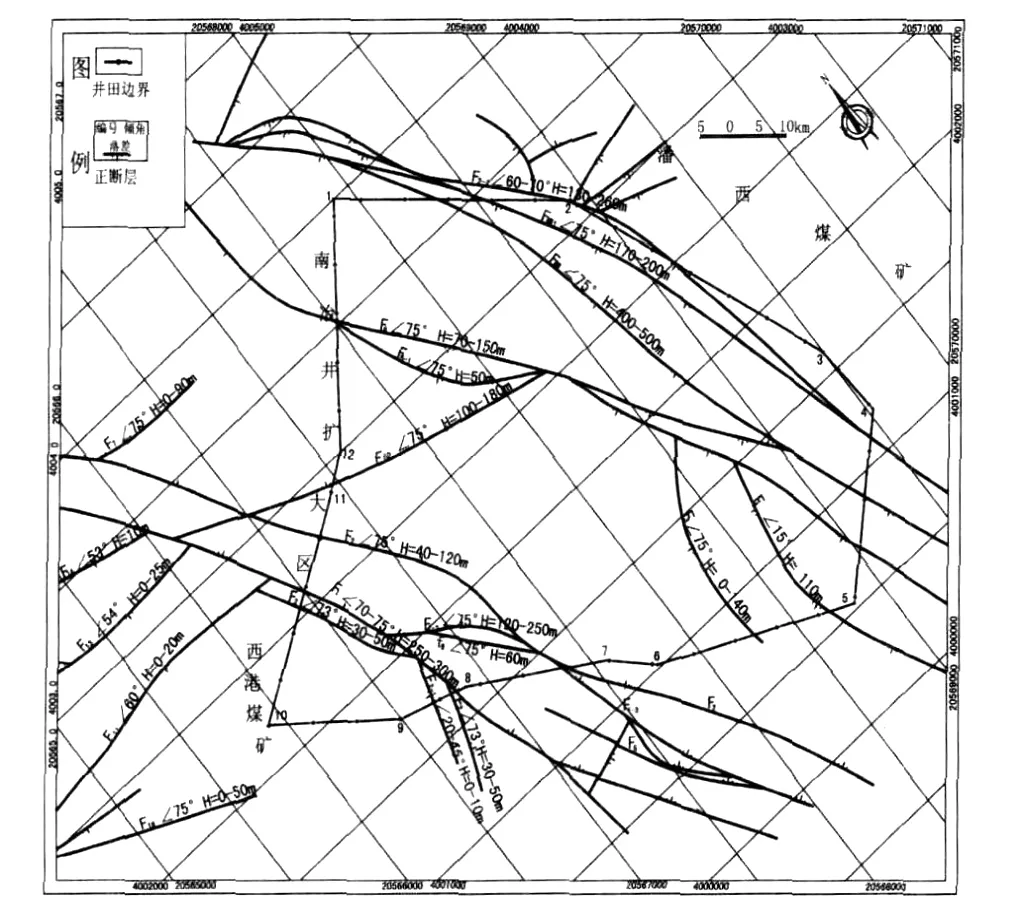
图1 东港井田构造纲要图

具体方法是:把东港井田按经纬网格以200 m×200 m的间距划分为169个评价预测单元,在每个预测单元内以边长为r的正方形格子构成网格平面去覆盖,分别计算r=100 m,r=50 m,r=25 m,r=12.5 m时的N(r)值,并算出lnN(r)与lnr之间的线性关系,由直线斜率求出盒维数D0,见表1(注:表1所列数据只是具有代表性的预测单元的信息)。

2.2 信息维法

由于盒维法仅仅统计了是否有断层通过的信息,对于通过的断层的个数没有进行研究,不能正确地反应预测单元中有一条断层通过时和多条断层通过时的区别,而信息维既考虑了预测单元内是否有断层穿过,也考虑到预测单元内断层的条数,因此,信息维数比盒维数更能反映断层体系空间分布的复杂程度和结构特征。

断层体系的信息维数定义为:

式中,Pi(r)为断层落入第i个尺度为r的盒子内的概率,令ni为第i个尺度为r的盒子内的断层条数,N为盒子总数,则这一概率为:

在实际计算中,令I1(r)=-∑Pi(r)lnPi(r),用实测的一系列(I1(r),r)值,通过最小二乘法拟合得I1(r)与lnr之间的线性关系:

则可由直线斜率求出信息维数D1。

在对研究区进行单元划分的基础上,分别计算r=100 m,r=50 m,r=25 m,r=12.5 m时的I1(r)值,由I1(r)与lnr之间的线性关系,求出信息维数D1,见表1。

由表1可以看出具有代表性的预测单元的分形维数分布范围在1.252～1.913之间,且各个预测单元分形维数的相关系数绝对值均大于0.990,良好的线性拟合关系说明了19#煤层断裂的分布在所采用的标度下具有良好的统计自相似性,从而表明了断裂构造具有分形特征,不同的分形维数大小体现了不同断层的复杂程度。同时还可以看出当预测单元中只有一条断层通过时,由两种方法计算所得的分形维数相同,例如表中的单元12,15,38等,但当预测单元中有多条断层通过时,计算所得的分形维数并不相同,例如表中的单元141、156等,这体现了两种方法在研究断层分形特征时所表现出来的差异。

3 19#煤层断裂构造分形特征分析

把预测单元的信息维数赋给相应块段的中心点,然后用样条插值,绘制出东港井田19#煤层断裂构造信息维数等值线图,将信息维数等值线叠合到构造分布图上进行分析对比,见图2。

对构造信息维数等值线与构造分布复合图进行分析可以发现:在井田中部由9、10、19、20、21、31、32、33、34、35、49、68单元,中西部由94、95、96、111、112、113、131、132、148、149单元所组成的区域中,断裂分布相对简单稀少,这一特性反映到信息维数等值线图中,恰好与信息维数D1≤0.4所圈闭的区域相对应。井田东部6、17、42、74单元,4、15、27、41、57单元,2、12、24、38、70、103单元;中部45、46、66、84、103单元,45、64、83、100单元;西南部90、109、127、144单元所组成的区域中,断裂规模大,总体呈北西-南东向展布,这一特性在相应的信息维数等值线图中与信息维数D1≥1.40的等值线所圈闭的区域相对应,且呈北西-南东向条带状延伸。由此可以看出,信息维数等值线图定量刻画了煤层断裂分布的复杂程度、分布范围及其展布方向,二者间具有良好的一致性。

表1 东港煤矿19#煤层断层分形维数表

图2 东港煤矿19#煤层构造信息维数等值线与构造分布复合图

4 19#煤层断裂构造复杂程度对开采的影响及未采区构造预测

东港井田由于受F1、F颜两大区域性断裂构造的影响,在区内单斜的基础上发育了较多的断层,对煤层切割破坏较严重,增大了煤层开采的难度,降低了煤田的经济价值。但同时也由于F1和F颜两断层的错断,使本区埋藏深度加大,客观上也使煤层免遭剥蚀,从而保护了本煤田。

除井田内的大中断层外,随工作面的开采揭露了大量小断层(如图2井田西南角139、140、141、142、143、154、155、156、157、158、167、168单元所围区域已采区揭露落差1～7 m小断层7条),小型断层成为影响本矿井正常生产的最重要因素。

井田西南角已采区域(即由139、140、141、142、143、154、155、156、157、158、167、168单元所围区域)信息维数范围为1.287～1.892,构造复杂程度为中等构造,以此为依据将研究区内构造划分为3种类型:信息维数在0～1.300,为简单构造;信息维数在1.300～1.900,为中等构造;信息维数大于1.900,为复杂构造,见图3。由图3可知,构造复杂区域主要分布在矿区的西北角,面积较小,矿区中东部及矿区西南部位为中等构造,矿区北部、中部、东边界和西南角部位构造为简单构造。

因此,矿井在设计施工时,应根据不同的构造复杂情况,采取不同的安全措施。值得注意的是井田西南角已采区的诸多小断层是在工作面开采过程中揭露的,由于受同一构造区域应力的影响,相邻未采区在开采过程中也会遇到一系列的小断层,这一点应该在施工过程中引起重视。

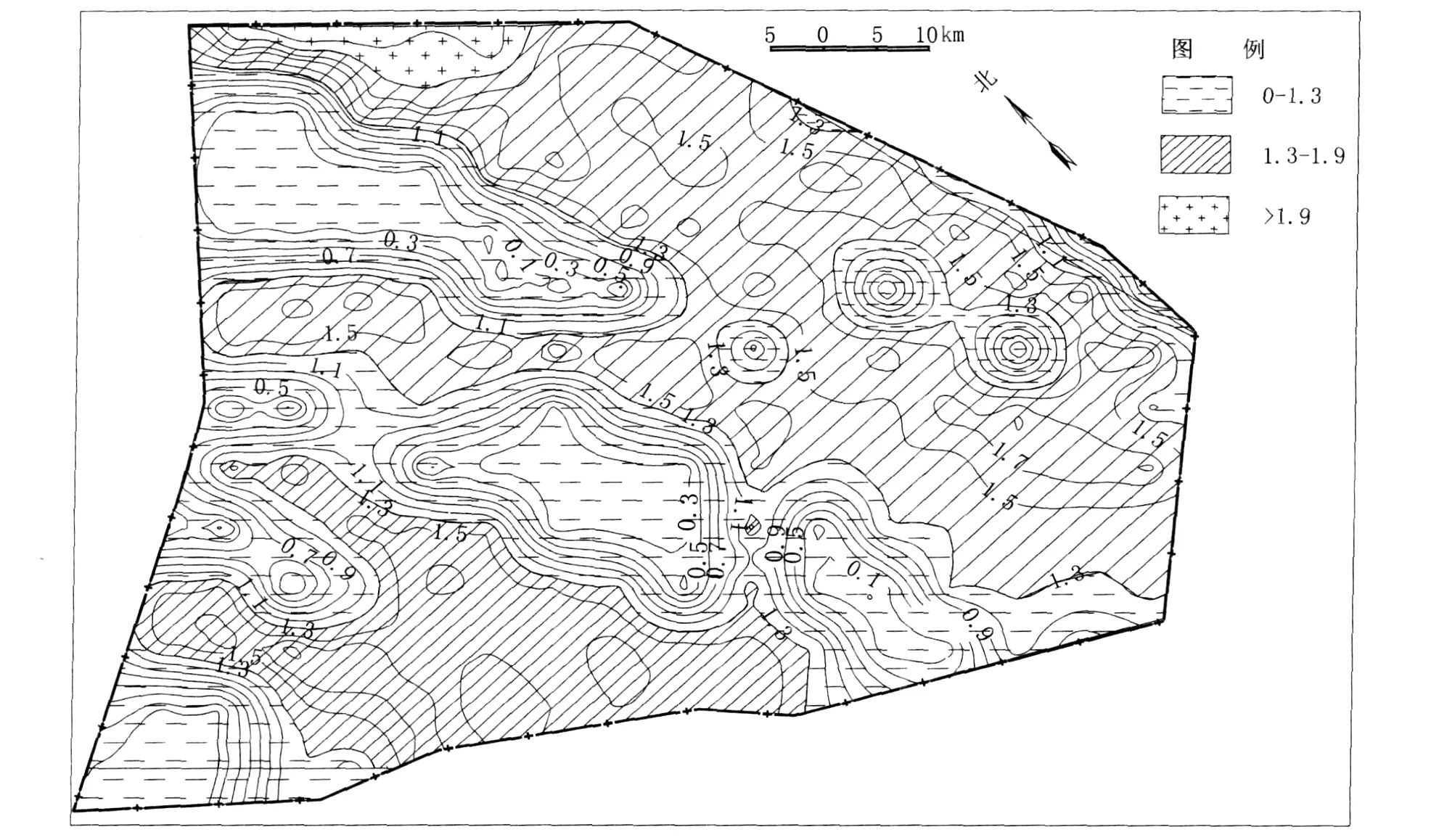
图3 研究区信息维数分区分布图

5 结论

(1)研究区内断裂构造具有很好的统计自相似性,构造的发育程度可以用分形理论进行定量研究。

(2)分形维数能够较合理、准确地反映井田断裂构造的密度、空间分布的均匀程度、断层的展布等信息,能较好地度量断裂构造的复杂程度。断裂强度较大,小断层及分支断层较多、断层密集的部位,分形维数较大;断层稀疏,小断层及分支断层相对少的部位,分形维数较小。

(3)通过对已采区构造的研究,对未采区的构造类型进行了定级,为煤矿开采提供了依据。

[1] 谢焱石,谭凯旋.断裂构造的分形研究及其地质应用[J].地质地球化学,2002(1)

[2] 谭凯旋,郝新才,戴塔根.中国断裂构造的分形特征及其大地构造意义[J].大地构造与成矿学,1998(1)

[3] 李本亮,张喜慧,孙岩等.断裂分维值对矿产资源预测的意义-以西藏地区为例[J].高校地质学报,1999(1)

[4] 卢新卫,马东升.湘中断裂体系分维与锑矿分布[J].地质论评,1998(5)

[5] 沈忠民,冯祖钧,周光甲等.断层体系分维与油田分布[J].地球科学-中国地质大学学报,1995(1)

[6] 葛灵生,胡宝林,汪宏志,徐德金.任楼矿井72煤层断层构造分形特征研究[J].安徽地质,2008(1)

[7] 曾联波,之钧,李京昌,汤良杰等.柴达木盆地北缘断裂构造分形特征与油气分布关系研究[J].地质科学,2001(2)

[8] 张建,王登红,孙宝生,陈郑辉.基于分形理论的成矿空间分析—以新疆东天山康古尔塔格金矿带为例[J].地球学报,2009,30(1)

[9] 刘锡大,赵希俊等.太行山山前断裂带的分形几何特征[J].地震研究,1998(2)

[10] 韩喜彬,李家彪,梁金城等.桂东南鸡笼顶矿田断裂系统分形研究[J].桂林工学院学报,2009(2)

[11] 陈江峰,胡诚.煤中断裂分布的分形特征[J].煤田地质与勘探,1999,27(1)

[12] 张均,周乔伟.川西北地区控矿断裂的分形特征及其预测意义[J].长春科技大学学报,2000(4)

[13] 卢新卫,马东升,孔兴功.湘中断裂分布空间结构的信息维特征初探[J].大地构造与成矿学,1999(1)