三类自激变换器及其解析结果
孙定浩
(北京控制工程研究所,北京100190)
三类自激变换器及其解析结果
孙定浩
(北京控制工程研究所,北京100190)
将三类基本的他激脉宽调制变换器(降压、升压、反向变换器)变为自激运行模式.给出三类相应的自激变换器(频率和脉宽调制)的电路拓扑及其解析结果.这将有助于扩大自激变换器在空间飞行器中的应用.
自激降压变换器;自激升压变换器;自激反向变换器
文献[1]描述了三类基本的变换器(降压、升压、反向变换器)均为他激调宽变换器.其组成中都有一个振荡器,它产生一个固定频率的方波以驱动变换器中起通/断作用的晶体管(或MOS管);另有一个反馈调节器,用它调节方波的占空比,以实现预定的目的.
本文提出三类变换器是将上述三类变换器变为自激运行模式,见图1所示.其组成的特点是,没有振荡器,只在电感元件中增设了一个绕组Nd:当磁芯中磁通量下降时,用Nd中的感应电流断开晶体管Q1;当这磁通量下降为零时,用Nd中产生的零电流信号触发Q1导通;当这磁通量上升时,用Nd中产生的感应电流驱动Q1.另有一个反馈调节器(图中用符号BCM表示),它调节Q1基流的幅值,从而调节Q1的导通时间,以实现预定的目的.
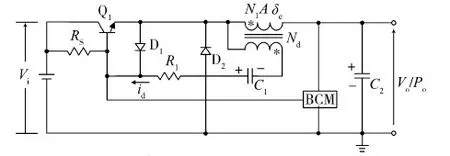
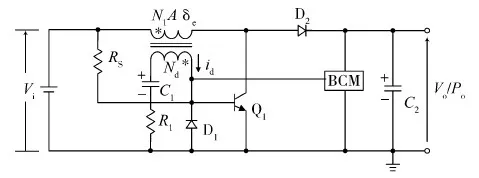

图1 三类自激变换器的电路拓扑
本文用能量传输的观点[2]分析这三类自激变换器.结果表明:当给定输入电压Vi,输出电压Vo和输出功率Po时,这三类变换器的运行特征参数——运行周期T和磁芯的最大磁通量密度B决定于图1中电感器的设计参数(指绕组匝数N1,磁芯截面积A和等效气隙长度δe).文中给出了以Vi、Vo、Po、N1、A、δe为变量的T和B的表达式,它们揭示了变换器的运行特性;也给出了以Vi、Vo、Po、A、T、B为变量的N1和δe的表达式,可供设计这三类自激变换器时参考.
1 三类自激变换器
图1给出三类自激变换器的电路拓扑.其中Q1作电开关使用,Rs是启动电阻.
当Q1导通,图1 (a):电源电压Vi施加在N1绕组和输出回路(指电容C2及其并联的负载电阻)串联的两端;图1(b)(c):Vi施加在N1绕组两端.此时Nd产生图示方向的感应电流id.基流调节器(BCM)将输出电压与给定值比较,其误差经放大去调节id,即调节实际流向Q1的基流幅值,以调节Q1的导通时间Ton.
当Ton结束,N1和Nd的感应电压方向同时倒向,Nd中感应电流id反向经D1流过,它使Q1维持在断开状态.此时,图1(a):N1耦合的磁能经D2释放到输出回路;图1(b):N1耦合的磁能和电压Vi的电能串联经D2释放到输出回路;图1(c):N1耦合的磁能经D2释放到输出回路.这个过程一直持续到磁能释放完毕为止,即Toff结束.
在Toff过程中,D1中流过的电流在C1上最终产生的电位差如图中所示方向;当Toff结束时,这个电位差触发Q1重新导通,重复上述过程.
2 运行特征参数
自激变换器在输入电压Vi,输出电压Vo和输出功率Po条件下运行.选择运行周期T,电感磁路中最大磁通密度B和占空比D作为变换器的运行特征参数.
磁能密度W为在相对导磁率μi,磁通密度B介质中单位体积所含的能量
式中μ0=4×10-7π.
注意到空气的相对导磁率最低μi=1,由式(1)可以推论,在相同的B值条件下,空气中磁能密度最高,空气是存储磁能的最佳物质;相对导磁率愈高,磁能密度愈低.
现在讨论磁芯(磁芯等效长度Le,截面面积A,导磁率μi)开空气隙(气隙长度δ)时磁能的分布.设磁路中磁通密度为B,由式(1)知,空气隙内磁能为
磁芯中磁能为
磁路内总磁能为
式中
将δe称为磁路的等效储存能量长度.
本文在以后分析中,对电感器以参数N1,Nd,A,δe表征,并忽略Nd的存在对能量传输的影响.因为这部分的功率消耗通常比输出功率小一个数量级以上.在这假定条件下,由磁路的安培环路定律可知,磁路中磁通密度为B(t)时,绕组N1通过的电流i(t)为
3 自激降压变换器
Ton为K导通时间,Toff为断开时间.
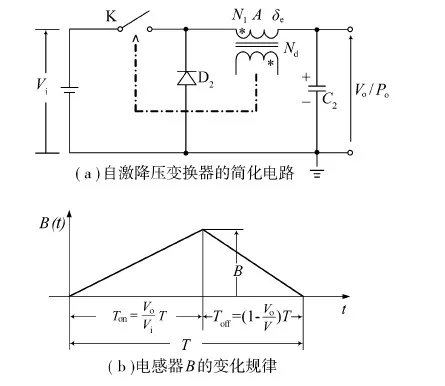
图2 自激降压变换器
由电磁感应定律得
从
得
根据图2(b)和式(6),在Ton阶段Vi向变换器提供的总能量为
这个能量将维持输出回路一个周期内的能量消耗,故有关系
将式(10)、(11)代入式(13)得
将式(14)代入式(11)得
由式(10)得占空比
由(14)~(16)描述了自激降压变换器的运行特征.
式(11)可改写成
将式(17)代入式(14)得
式(17)和式(18)供设计电感器时引用.
4 自激升压变换器

图3 自激升压变换器
图3给出自激升压变换器的简化电路.由电磁感应定律得
显然
由此得
由图3和式(6)知,在一个周期内,电源Vi向变换器提供的总能量为
这个能量将供一个周期内输出回路的消耗,故有关系式
将式(23)代入式(25)得
式(25)可改写成
由式(22)得
由(26)~(28)描述了自激升压变换器的运作特征.
式(23)可改写成
式(29)代入式(27)得
式(29)和(30)可供设计电感器时使用.
图4给出自激反向变换器的简化电路,它等同于自激反激变换器[2]中Ni与No绕组合为一个绕组.由电磁感应定律得
5 自激反向变换器

图4 自激反向变换器
显然
由此得
在Ton阶段,Vi向磁路提供的总能量为
Toff阶段,Vi不提供能量.因此式(36)的能量将维持输出回路一个周期的消耗,故有关系
将式(35)代入式(37)得
式(38)代入式(35)得
由式(34)得占空比
式(38)~(40)描述了自激反向变换器的运作特征.
式(35)可改写成
式(41)代入式(39)得
式(41)和(42)可供设计电感器时使用.
6 结 论
自激变换器具电路简单,元件少(特别是无需PWM集成电路),小功率输出时效率高以及可靠性高等特点.从上世纪80年代开始在中国空间飞行器应用.
本文为构建自激变换器提供了更多的电路拓扑.期望这有助于推动自激变换器在空间飞行器中的应用.
[1] 蔡宣三,龚绍文.高频功率电子学[M].北京:科学出版社,1993
[2] 孙定浩.新建自激反激变换器方程及其解析解[J].航天控制,2001,19(1):48-54
ThreeKindsofSelf-OscillatingConvertersandTheirAnalyticalResults
SUN Dinghao
(BeijingInstituteofControlEngineering,Beijing100190,China)
The paper is to make three kinds of fundamental PWM (pulse-width modulation) converters (buck, boost, buck-boost) self-oscillate.Three kinds of circuit topologies of self-oscillating converters (corresponding to the PWM converters) and their analytical results are given.It would be helpful to widen self-oscillating converters to be used in the space vehicles in china.
self-oscillating buck converter; self-oscillating boost converter; self-oscillating buck-boost converter
2009-11-17
孙定浩(1934—),男,扬州人,高级工程师,研究方向为电功率变换技术(e-mail: sundinghao@bice.org.cn).
V242.4+31
A
1674-1579(2010)02-0055-03

