卫星编队飞行相对轨道动力学模型的比较及选用
苏 晏,黎 康
(1.北京控制工程研究所,北京 100190;2.空间智能控制技术国家级重点实验室,北京100190)
卫星编队飞行相对轨道动力学模型的比较及选用
苏 晏1,2,黎 康1,2
(1.北京控制工程研究所,北京 100190;2.空间智能控制技术国家级重点实验室,北京100190)
基于动力学方法推导了几种编队飞行相对轨道动力学模型.分析比较了引力项线性化以及J2摄动引起的模型误差的数量级,给出了模型选取的参考准则以及适用条件,分析了不同模型的适用性.最后选取太阳同步轨道和静止轨道作为数值算例,选取合适的相对轨道动力学模型,验证模型选取准则的有效性.仿真结果表明一定范围内考虑J2摄动能提高精度,而超出一定范围J2的引入只会增加复杂性,因此提出的模型选取准则对相对轨道动力学模型的选取有一定的参考价值.
相对轨道动力学;J2摄动;误差分析
现代小卫星已有几十年的发展历史,小卫星具有一系列应用优势如重量轻、体积小、成本低、机动性好、生存能力强等[1].作为小卫星应用的一个重要方面,小卫星编队飞行技术也被普遍认为是未来小卫星应用模式的必然趋势.小卫星的编队飞行实质上是利用多颗飞行中的小卫星组成一定形状,各颗小卫星之间通过星间通信相互联系、协同工作,共同承担空间信号的采集与处理以及承载有效载荷等任务,整个星群构成一个满足任务需要的、规模较大的虚拟传感器或探测器[2].
相对轨道动力学模型是编队飞行领域研究的基础性问题,特别是线性化后的相对轨道动力学模型,由于其形式简单,在构型设计、相对轨道控制方面应用广泛.构建轨道动力学模型时,模型的误差主要来自两方面,即引力项线性化误差以及J2摄动未建模误差.目前,相对轨道动力学建模的普遍做法是在引力项线性化的基础上考虑J2摄动项以提高模型精度,如CW-J2、TH-J2模型等[3].但实际上笔者发现,在一定范围内,这样做有利于模型精度的提高,但超出一定范围,J2项摄动的影响要小于引力项线性化产生的误差影响,因此过分追求在模型中加入J2项影响并无太多意义,只会使模型更为复杂.
本文首先推导了几种相对轨道动力学模型.其次通过数学方法分析了J2摄动未建模会引入的模型误差以及引力项线性化引入的模型误差.接下来给出了动力学模型的选用参考准则.最后通过数学仿真验证模型选用参考准则的有效性,并对真实卫星的相对运动进行了仿真验证.
1 相对轨道动力学建模
1.1坐标系定义
航天器编队飞行动力学分析过程中假设有两颗航天器,一颗为基准星,另一颗为编队星.研究编队飞行动力学涉及如下两个坐标系:
(1) 地心惯性坐标系:原点位于地心O,X轴位于赤道面内指向春分点,Y轴位于赤道面上并与X轴垂直,Z轴与X和Y轴构成右手坐标系.
(2) 编队飞行基准星轨道坐标系:原点位于基准星中心o,xy平面在中心卫星轨道平面内,y轴沿中心卫星速度方向,x轴沿地心与中心卫星的连线背向地心,z轴与xy平面构成右手坐标系.
1.2精确动力学模型
地球引力位函数的一般表达式如下[4]:
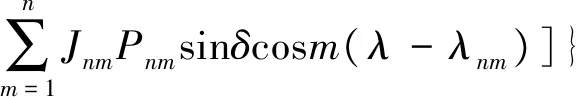
式中,μ为地球引力常数,RE是地球平均半径,r是地心距,λ、δ分别是地心经度和地心纬度,Pn、Pnm为勒让德多项式,Jn为带谐项系数,Jnm为田谐项系数.
动力学方程如下:
式中,r为地心距矢量,r为卫星地心距,μ为地球引力常数,a表示实施的控制加速度,b表示摄动加速度.
令r=R1-R0表示编队星相对于基准星的位置矢量,联立得到精确动力学模型表达式如下:
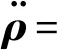
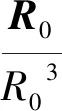
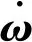
1.3不考虑摄动的相对轨道动力学模型
不考虑摄动力对卫星轨道的影响(即b0=b1=0),角速度和角加速度如下:
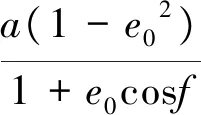
若在如上前提下假设相对轨道动力学的引力项线性化的条件存在,对引力项取线性近似,线性化过程如下[5-6]:
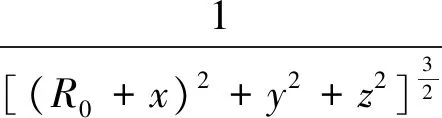
1.4考虑J2摄动的相对轨道动力学模型
考虑J2摄动对相对轨道影响得到J2摄动影响下的角速度及角加速度如下[7]:

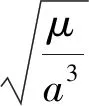
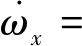
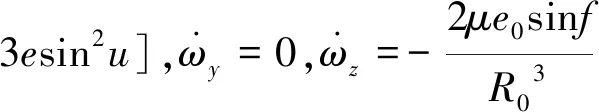
考虑J2项影响情况下,引力位函数如下:
以上各式与式(3)进行联立可得到考虑J2摄动对相对轨道影响下的相对动力学方程.
2 J2引力摄动项及引力项线性化引起的误差分析比较
2.1J2引力摄动项引起的误差数量级分析
由以往分析结果可知,J2项摄动力对相对轨道的影响以漂移为主[8-10].带谐项摄动力引起的摄动加速度在基准星轨道坐标系上的分量为[6]:
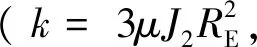
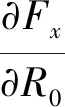
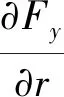
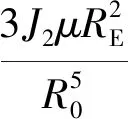
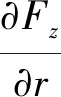
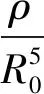
2.2引力项线性化引起的误差数量级分析
引力项线性化引起的误差在基准星轨道坐标系上分量为:
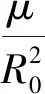

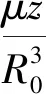
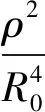
3 模型选取准则
由2.1和2.2节的分析可知,取各自误差数量级如下:
定义比例因子如下:
根据比例因子取值范围的不同,可分如下三种情况进行讨论.
1) 比例因子α≪1
此种情况下引力项线性化引起的加速度误差数量级高,J2摄动项的引入会增加模型的复杂度且对模型精度没有决定性影响,相对轨道动力学模型建立过程中没有必要引入J2摄动项.
2) 比例因子α≫1
此种情况下J2摄动引起的加速度误差数量级高,J2摄动项的引入可以在很大程度上提高模型精度,相对轨道动力学模型建立过程中可以在引入J2摄动项的同时对引力项进行线性化.
3) 比例因子α介于中间值
此种情况下J2摄动引起的加速度误差数量级与引力项线性化引起的加速度误差数量级相当.若追求模型高精度,则相对轨道动力学模型建立过程中在引入J2摄动项的同时不能对引力项进行线性化,模型使用精确模型;建模过程中若追求模型简洁度,则模型建立中不考虑J2摄动影响同时对引力项进行线性化.
以上讨论模型建立中的选取准则是有一定的适用范围的.卫星模型建立后,加速度误差会随时间积累为位置误差,J2摄动引入的长期累积误差较引力项线性化引入的长期累积误差明显,使得比例因子发生改变,模型选取准则不适用.故本文所讨论的模型选取准则是基于小范围时间累积的前提之下的.
4 仿真算例与分析
选取基准星运行轨道为太阳同步圆轨道,对星间相对运动四分之一周期内J2摄动引起的位置误差和引力项线性化引起的位置误差进行仿真.选取轨道参数如下:半长轴a=RE+800 km,轨道倾角为i=98.6°,偏心率e=0,初始时刻升交点赤经Ω=0,近地点幅角ω=0,绕飞半径r=1km,比例误差因子α=18.407 3>10≫1.为保证相对轨道运动为封闭曲线,选取初始值如下:x0=r,y0=z0=0,vx0=vz0=0,vy0=-0.002 1(线性模型初值),vy1=-0.002 1(非线性模型初值)[11],仿真结果如图1~图2所示.
仿真结果表明比例因子α≫1情况下,小轨控周期内J2摄动项引起的累积误差数量级高,控制模型选取过程中要考虑J2摄动项影响.
选取基准星运行轨道为静止圆轨道,对星间相对运动进行仿真,选取轨道参数如下:半长轴a=RE+36 000km,轨道倾角为i=0,偏心率e=0,初始时刻升交点赤经Ω=0,近地点幅角ω=0, 绕飞半径r=100km.得到比例因子α=0.031 2<0.1≪1.初始值选取如下:x0=r,y0=z0=0,vx0=vz0=0,vy0=-0.014 5(线性模型初值),vy1=-0.014 5(非线性模型初值),仿真结果如图3~图4所示.
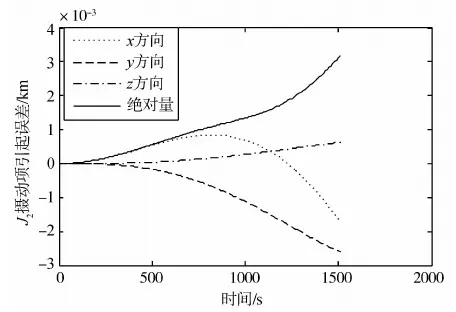
图1 太阳同步圆轨道1/4周期内J2摄动误差

图2 太阳同步圆轨道1/4周期内引力项线性化误差

图3 静止轨道1/4周期内J2摄动误差
仿真结果表明比例因子α≪1情况下,小轨控周期内引力项线性化引起的累积误差数量级比J2摄动项引起的累积误差数量级高,为降低模型复杂度,模型建立过程中没有必要引入J2摄动项影响.
5 结 论
本文建立了4种相对轨道动力学模型,从理论上对J2摄动项以及引力项线性化引起加速度误差的数量级进行了量化比较,给出了比较参数比例因子的定义,分析了相对轨道动力学模型建立过程中J2摄动项以及引力项线性化引起误差的主导性作用,给出了相对轨道动力学模型选取的准则,给出了准则的适用条件.最后通过数学仿真对理论进行了验证.仿真结果表明,卫星实际相对轨道运动情况与本文所提出的模型选取准则相符,比例因子在一定范围内模型建立过程中考虑J2摄动影响可以提高模型提高精度,而超出一定范围时J2摄动影响的引
入只会增加模型复杂性而对模型精度没有决定性影响,本文提出的相对轨道动力学模型的选取准则有一定的参考价值,为以后构型设计、相对轨道控制器设计中的模型建立提供了依据.
[1] 林来兴.ST-5微小卫星编队与星座及其空间飞行验证[J].航天器工程,2007,16(1):63-68
[2] 闻新,马文弟,周露.小卫星编队飞行的应用模式分析及展望[J].中国航天,2005(8):40-43
[3] 杏建军.编队卫星周期性相对运动轨道设计与构形保持研究[D].国防科学技术大学,2007
[4] 章仁为.卫星轨道姿态动力学与控制[M].北京:北京航空航天大学出版社,1998
[5] 林来兴.卫星编队飞行精确动力学模型与三维定位系统[J].宇航学报,2008,29(3):831-837
[6] 林来兴,车汝才.航天器编队飞行动力学模型和精度分析[J].航天器工程,2008,17(2):19-25.
[7] 耿长福.航天器动力学[M].北京:中国科学技术出版社,2006
[8] 孟鑫,李俊峰,高云峰.卫星编队飞行中相对轨道的J2摄动分析[J].力学学报,2006,38(1):89-95
[9] 孟云鹤,韩宏伟,戴金海.J2摄动作用下近地轨道卫星编队构形长期演化机理分析[J].宇航学报,2007,28(2):253-258
[10] Schaub H,Alfriend K.T.J2invariant relative orbits for spacecraft formations[J].Celestial Mechanics and Dynamical Astronomy.2001,79(5): 77-95
[11] Fang R,Zhang S J,Cao X B.Relative dynamics and initialization condition of spacecraft formations in eccentric orbits [J].Aircraft Engineering and Aerospace Technology,2006,78(6):481-489
ComparisonandSelectionofSpacecraftFormationFlyingRelativeOrbitDynamicsModels
SU Yan1,2,LI Kang1,2
(1.BeijingInstituteofControlEngineering,Beijing100190,China;2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190,China)
Based on the dynamics,several spacecraft formation flying relative orbit dynamics models are established in this paper.And then,error orders of magnitude leaded by theJ2perturbation and linearized gravitation are analyzed and compared.Reference rules for model selection and their applicable conditions are proposed.Applicability of different models is analyzed.At last based on two groups of parameters referred to solar synchronization orbit and GEO,dynamics models are selected according to the proposed reference rule,and mathematical simulations are carried out to verify the rule.The simulation results indicate that in a certain range the import ofJ2perturbation will improve accuracy of model while in some range it will only lead high model complexity and the proposed method in the paper has a certain reference value for relative orbit dynamics model choosing.
relative orbit dynamics;J2perturbation; error analysis
2010-03-20
苏晏(1987—),女,河北人,研究生,研究方向为控制理论与控制工程 (e-mail: yansu11@hotmail.com).
V448.2
A
1674-1579(2010)04-0054-05

