复杂推力器配置控制能力的性能指标及其应用*

王 敏，解永春

(1.北京控制工程研究所,北京100190；2.空间智能控制技术国家级重点实验室,北京100190)

复杂推力器配置控制能力的性能指标及其应用*

王 敏1,2，解永春1,2

(1.北京控制工程研究所,北京100190；2.空间智能控制技术国家级重点实验室,北京100190)

针对多个推力器斜装且耦合强的复杂配置情况，首先基于矩阵范数理论提出一种适用于分析复杂推力器配置控制能力的性能指标——最小上界指令，给出其计算公式，并通过算例验证了该性能指标在评价配置控制能力的有效性；然后讨论推力矢量的幅值和几何分布对于该性能指标的影响；基于该性能指标，建立一个含参数配置阵的优化设计非线性规划模型，讨论了以增强配置控制能力为目标进行配置参数优化设计的方法.

推力器; 配置; 控制能力; 优化设计; 最小上界指令

推力器的配置一般指航天器上配备的所有推力器的数量、推力大小、安装位置和指向等.而推力器配置的控制能力则是指配置所能产生的控制指令的分布范围.推力器配置的控制能力分析对于配置的选择和设计都具有极其重要的意义.国内以往对于推力器配置控制能力的分析主要是根据推力器控制指令分配算法(推力器选择逻辑)将推力器进行解耦分组[1]，使得每个组合仅在一个控制量方向上产生作用，从而简单求得配置在各控制量方向上的控制能力.国外这方面的理论研究也大都集中在针对已知配置判断其能否生成空间任意方向的控制指令[2-3]，即配置的控制能力在方向上的全面性，而没有考虑推力器所能产生的指令幅值大小的有界性.对于配置构型确定后有界控制能力范围的研究，一般都靠数值仿真来确定[4-5]，尤其对于任务维数高的情况，理论研究结果很少.近年来，随着交会对接等复杂航天技术的进一步发展，航天器的推力器配置也日趋复杂化，主要体现在推力器数量日益增多以及推力器斜装产生的各控制分量间耦合加强的情况[6]，加之推力器选择逻辑的进一步复杂化，这就给推力器配置的控制能力分析及配置设计造成了一定困难.

本文的主要研究目的在于给出一种评价复杂推力器配置控制能力的性能指标，用以评价不同推力器配置的控制能力，并以此为优化指标指导推力器配置的优化设计.文章首先提出一种适用于复杂推力器配置控制能力分析的性能指标——最小上界指令；然后讨论推力器的配置因素对该性能指标的影响；最后基于该性能指标,对推力器配置参数的优化设计问题进行了初步探索.

1 反映配置控制能力的性能指标——最小上界指令

1.1前提条件

要研究推力器配置的控制能力就不得不提到推力器配置的控制指令分配算法.从航天器的所有推力器中选出能实现控制指令的推力器组合，并计算出组合中每台推力器的工作时间，称为推力器的指令分配.指令分配处于生成控制指令的末环，配置的控制能力正是通过指令分配算法控制各推力器喷气才能最终实现，故指令分配方式的优劣直接影响配置的控制能力能否充分发挥.

推力器的指令分配问题一般描述为，求解合适的t≥0,使其满足等式

显然当n>m(即推力器个数多于任务维数)时，该问题有无穷多组解，于是存在一个如何选择合适解的问题.目前针对推力器的指令分配算法主要有传统解耦法[1]、伪逆法[3,7]、线性规划法[1,2,7]及最优查表法[4,6,8]这几种.其中传统解耦法和伪逆法虽然在线计算速度快，但推力器对消较多使得推力器的使用效率低下.而线性规划法和最优查表法能充分利用推力器各分量间的耦合，从而能在实现控制指令的同时减少对消，提高推力器使用效率，充分发挥配置的控制能力.尤其最优查表法在线性规划法的基础上将其离线化，从而大大提高了在线计算速度，更具工程应用价值.

故本文给出的最小上界指令这一性能指标及其相应计算方法，是在以线性规划法或最优查表法为指令分配方法的前提下得到的，其意义在于：①这两种方法能更充分地发挥配置的控制能力，故以其为前提得到的性能指标能更好地反映配置最本质的控制能力.②其他传统指令分配方法的控制能力分析较为直观和简单，而这两种指令分配算法较为复杂，针对它们的控制能力分析目前仅有一些数值仿真讨论，尚无理论分析结果.

1.2最小上界指令的提出及计算方法

虽然复杂的配置和指令分配算法使得配置的控制能力上界范围很难实现精确的解析描述，但在有界控制能力范围的上界中必然存在一个模值最小的控制指令，如图1中的umin所示，称其为最小上界指令.它的模值能在一定程度上反映配置控制能力的大小，其指令向量本身则指示出配置控制能力最弱的方向，从而在一定程度上有助于实现复杂配置控制能力的量化比较.

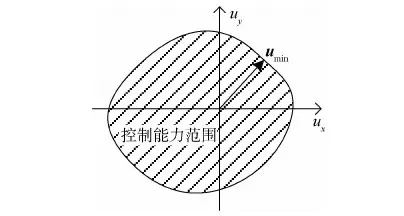
图1 最小上界指令示意图

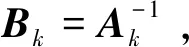
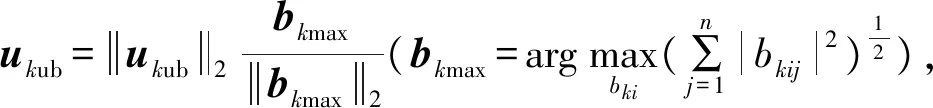
定理的详细证明过程可参考文献[10].由该定理及其证明过程可得A阵的最小上界指令为：

式中ukub为p个推力器组合分别对应的子配置阵Ak的最小上界指令，其计算分如下两种情况：

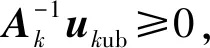
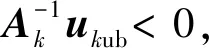
1.3算例

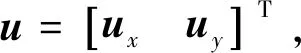
其第1到第4列分别对应4个推力器矢量T1～T4，如图2所示.根据最优推力器组合表生成算法[9]，可得到其全部最优推力器组合如下：

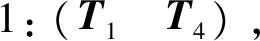
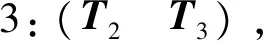
其两个行向量及其对应的欧式范数分别为

取二范数最大的第二行，于是有

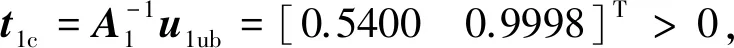
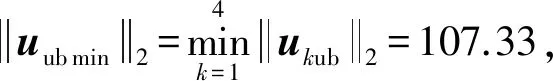
这与矩阵范数的计算结果完全一致，从而验证了最小上界指令计算方法的正确性.该最小上界指令其实就是从原点到边界线ux+2uy=240的垂线，如图2上虚线矢量uubmin所示.

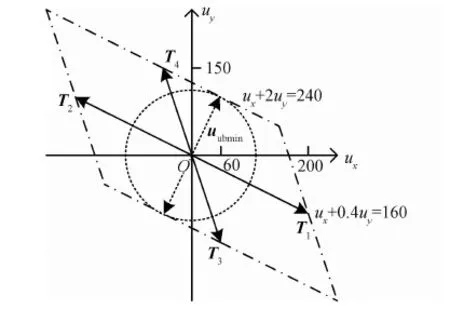
图2 控制能力范围

2 影响最小上界指令的配置因素

从式(2)可以看出，推力器最小上界指令的模值与推力器的工作时间上界tmax以及推力器的配置阵A有关.在配置构型确定的情况下，最小上界指令的模值与tmax成正比关系.这从物理上很容易理解：tmax越大，允许的推力器工作时间越长，其能实现的冲量也就越大，控制能力就越强.但tmax与系统控制周期等因素相关，一般不宜改动，故欲提高配置的控制能力，应着重从配置的几何构型，即改变A阵来考虑.

2.1推力矢量幅值对最小上界指令的影响

增大推力矢量的幅值反映在A阵中就是给A的列分别乘以不同的系数，即新的配置阵变为

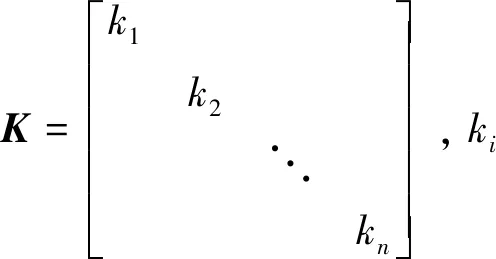
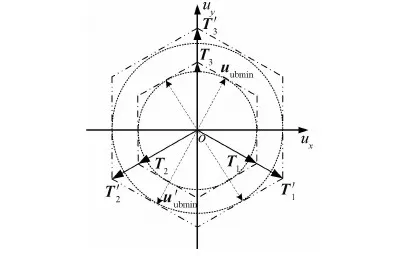
图3 推力矢量幅值对最小上界指令的影响

2.2推力矢量的几何分布对最小上界指令的影响

这里的几何分布主要指推力器矢量在指令空间中的指向，它对控制能力范围的影响较复杂，无法用简单的增大或减小来概括.比如下图4中的两个推力矢量T1、T2，设T1沿x轴正向，T2在平面内以O为圆心旋转，两者合成的控制能力范围也随之旋转，如图中的平行四边形所示.可以看出，随着T2指向的变化，控制能力范围的变化使它们互有交集，但并非包含与被包含关系.尤其对于维数高的情况，控制能力范围的变化会更加复杂，需根据具体情况具体分析.

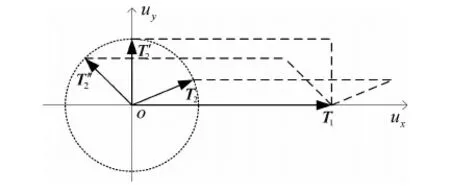
图4 推力矢量几何分布对控制能力范围的影响

3 增强控制能力的配置优化设计

3.1问题的描述

推力器配置的最小上界指令体现了配置最弱的控制能力水平.我们在进行配置设计的时候，在有限的条件下，一般希望设计出的配置其控制能力尽可能的强.此时，就以最小上界指令模值尽量大作为优化目标，对配置中的某些可变参数进行优化设计，从而实现有限条件下控制能力的最大化.该问题可用下面的非线性规划模型来描述：

φ∈[φm，φM]

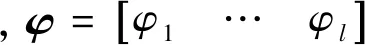
图5 f(φ1,…,φl)映射关系示意图

3.2仿真算例

设某一配置有18个推力器的6维任务，其配置阵A已知，即各推力器的额定推力以及初始的安装位置坐标和安装倾角都已知.在任务仿真中发现对某些方向的控制指令进行指令分配后得到的工作时间超出了推力器工作时间的上界，经查得知是在滚动方向上出现了控制能力不足的现象.配置在滚动方向的力矩主要由推力器T15～T18来实现，于是最简单的方法就是加大该推力器额定推力的大小.但当推力大小无法改变时，也可通过改变相关推力器的安装位置、倾角等参数，来局部修改推力器配置的几何构型，从而扩大其指令域范围，增强配置的控制能力.

画出T15～T18的局部推力器配置如图6所示，假设一个安装相位角参数φ1和倾角参数φ2.根据这两个参数和已知的配置信息，原配置阵中第15到第18列相应变为如下带有配置参数的形式：

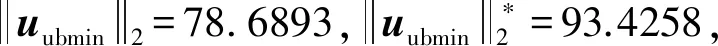
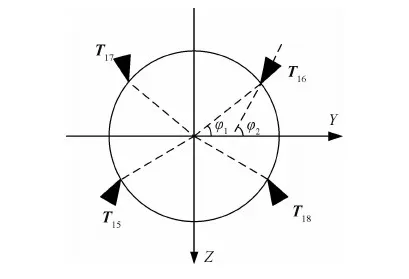
图6 滚动方向局部配置示意图

另外，从图7以及带参数的配置阵可以看出，当满足φ2-φ1=90°时，配置在Mx方向的控制量就能达到最大值，因为此时力臂最长.但该算例的最优解并不唯一，这一点也可以从图8看出，配置的最小上界指令模值随这两个角度参数的改变而不断变化.它同时也说明，位置和倾角的变化对最小上界指令大小的影响有限.

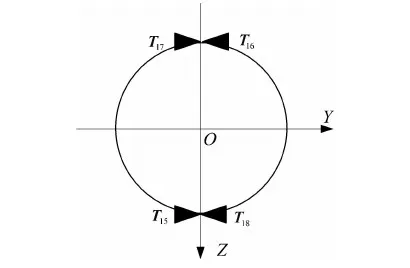
图7 优化后的局部配置图

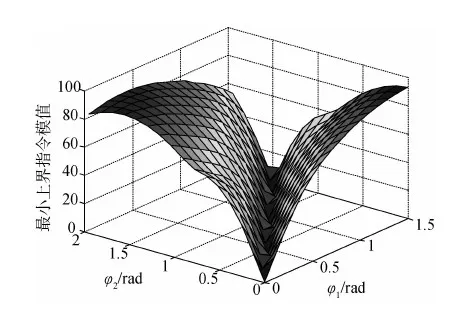
图8 最小上界指令模值随φ1,φ2变化图

4 结 论

本文给出了评价复杂推力器配置控制能力的最小上界指令，它在一定程度上有效反映不同推力器配置控制能力的强弱，对于实现复杂配置控制能力的量化比较具有一定意义.以此为优化目标对配置的某些局部参数进行设计寻优确实可以提高配置在局部区域内的控制能力，这也为进一步研究推力器配置的综合设计及优化提供了参考.

[1] 黄圳圭.航天器姿态动力学[M].北京: 国防科技大学出版社,1997

[2] Crawford B S.Configuration design and efficient operation of redundant multi-jet systems[C].AIAA Guidance Control and Flight Mechanics Conference,Princeton,Aug 1969

[3] Ricardo S S P,Roberto A,Pablo A A.Robust optimal solution to the attitude/force control problem[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(3): 784-791

[4] Ankersen F,Wu S F.On optimization of spacecraft thruster management function[C].AIAA Guidance,Navigation and Control Conference and Exhibit,Rhold Island， Providence ,Aug 2004

[5] Pablo A.Servidia.Control allocation for gimballed/fixed thrusters [J].Acta Astronautica,2009(7)：23

[6] Martel F.Optimal simultaneous 6 axis command of a space vehicle with a precomputed thruster selection catalogue table[C].AAS/AIAA Astrodynamical Specialist Conference Meeting,Montana,Aug 2003

[7] Daniel B.Six-dimensional thruster actuation and configuration design for spacecraft[J].Advances in the Astronautical Sciences,2007,128: 929-945

[8] Wang M,Xie Y C.Design of the optimal thruster combinations table for the real time control allocation of spacecraft thrusters[C].The 48thIEEE Conference on Decision and Control,Shanghai,China,December 16-18,2009

[9] 张兵,吴宏鑫.单向执行器系统配置的完整性[C].中国控制会议,浙江宁波,1998,8

[10] 王敏,解永春.航天器复杂推力器配置控制能力分析的一种新方法[J].中国科学E辑,2010,40(8): 912-919

APerformanceIndexforControlCapabilityofComplexThrusterConfigurationsandItsApplication

WANG Min1，2,XIE Yongchun1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China；2.NationalKeyLaboratoryofScienceandTechnologyonSpaceIntelligentControl,Beijing100190,China)

A new performance index for assessing the control capability of complex thruster configurations (non axis-symmetric configuration with coupling effects) is proposed,which is denominated as the least upper bound control command in this paper.Formula for calculating this index is deduced based on the matrix norm theory,and configuration factors affecting the index are discussed.This index is used as an objective function,and a non-linear programming model for the optimal thruster configuration design is established.Finally,a thruster configuration example is given to demonstrate its validity.

thruster; configuration; control capability; optimal design; least upper bound control command

V448.22

A

1674-1579(2010)04-0036-06

*国家自然科学基金(90305024)资助项目.

2010-05-10

王敏(1981—),女，湖北人，博士研究生，研究方向为航天器控制 (e-mail: amethyst0210@126.com).